CWOI 杂题选做(23Jul,23Aug)
麻了这集训怎么改的完题啊。
如果我觉得实现很简单的就不放代码,甚至可能就是口胡。
细节比较复杂的我会写一写。
如果实在没时间我就直接贺代码,前提是确保如果出原题我能写出来。
也有一种可能是太忙了没来得及放代码。
如果有 § 标记的说明我认为这个题很趣味。
如果是 §§ 就说明我认为这个题是神题。
SGU311 Ice-cream Tycoonψ(`∇´)ψ
商店里初始时没有物品,支持以下两种操作
增加 \(n\) 个价格 \(c\) 的物品
对于一名想用 \(t\) 元钱购买前 \(n\) 便宜的物品的顾客,若这些物品总价不超过 \(t\) 则从商店中移除,否则不做操作,
\(1\le n, c \le 10^6, 1\le t \le 10^{12}\)
Memory Limit: 64MB
送分复健题。
考虑权值线段树维护,每次线段树二分找到对应位置。
然后前缀求和并区间修改即可。
CF620E New Year Treeψ(`∇´)ψ
给一颗 \(n\) 个节点的树,现在每个节点上有一个颜色 \(c_i \le 60\)。
有 \(m\) 个查询:
把一个子树中所有的节点都赋成同样的颜色
求出一个子树中出现过的颜色个数。
\(1\le n, m\le 4\times 10^5\)。
也是简单题,子树整体操作很容易思考到使用 dfn 转成序列问题。
注意到 \(c_i \le 60\),可以对每个位置维护一个二进制状态,使用线段树维护这个状态即可,你可以看作弱化版的雨天的尾巴(那题线段树维护的是线段树不是类似 bitset 状物)。
CF487E Touristsψ(`∇´)ψ
有 \(n\) 个点 \(m\) 条边的无向图,每个点有权值 \(w_i\)。
你需要支持两种操作:
修改一个点的权值。
查询从 \(u\) 到 \(v\) 的路径,不经过重复点,可能去到的点中最小的权值。
\(1\le n, m, q \le 10^5, 1\le w_i \le 10^9\)。
在图上做这种路径查询操作以及单点操作是困难的。
注意到“不经过重复点”,这给了我们一个提示,如果是不经过重复边就可以缩边双。
然后缩完之后就得到了一颗树,对这个树做树链剖分即可。
但是这里是点双,直接缩是不行的,因为一个点可能在多个点双连通分量里面。
于是这里有一个技巧,有一种叫圆方树的数据结构,可以把这个问题转成树上的。
具体操作可以看看我的博客。
然后建出圆方树之后,问题就转化为了树上查询。
我们不妨把方点的权值设为与它相连的节点的权值的最小值。
然后每次单点修改就行了。
但是一个问题是,如果我们修改的是割点,它会和很多个方点相连,这样就被卡到 \(O(n^2)\) 了,所以有一个技巧。
我们令方点维护的是以某个圆点(比如 \(1\))为根的时候,它的儿子圆点的权值最小值,这个维护一个 multiset 就可以了。
然后询问的时候只需要考虑 \(\text{LCA}(u, v)\) 是不是方点,如果是方点,还需要在路径询问的基础上和 \(\text{father}(\text{LCA})\) 的权值取 \(\min\)。
这个是 Trivial 的。
CF1284D New Year and Conference §ψ(`∇´)ψ
给 \(n\) 个演讲,第 \(i\) 个演讲在两个报告厅中举行
第一个报告厅中的开始时间是 \(sa_i\),结束时间是 \(ea_i\),
第二个报告厅中的开始时间是 \(sb_i\),结束时间是 \(eb_i\)。
问有没有演讲的子集 \(S\),使得所有 \(S\) 中的演讲都是在一个报告厅中不存在重叠,在另一个中重叠?
\(1\le n \le 10^5\)。
一个巧妙做法,我们维护两个集合 \(S_A,S_B\),分别表示在 \(A,B\) 中会重叠的所有区间对 \((i, j)\)。
然后问题答案为 YES 当且仅当 \(S_A \not= S_B\),这是显然的。
然后怎么维护区间呢?这个东西是 \(O(n^2)\) 的,不好做,但是,我会哈希!
设计 Hash 函数 \(H(S) = \sum\limits_{(i, j) \in S}^{}v_i \times v_j\)。
其中 \(v_i, v_j\) 是随机分配的权值,也可以是 \(v_i = i\) 这样的。
然后我们算贡献的时候用 set 什么的数据结构整体处理可以 \(O(n \log n)\) 。
还有一个更好写的 Hash 做法,等会写。
QOJ2065 Cyclic Distance §ψ(`∇´)ψ
你有一棵树,无权,定义 \(dis(u, v)\) 表示树上 \(u, v\) 两点的最短路。
你现在需要选出 \(k\) 个点按一定顺序构成一个环,环上相邻两点的距离为它们的树上 \(dis\),最大化这个环的权值和。
\(T \le 10^5, \sum n \le 2\times 10^5\)。
首先考虑,原问题的限制可以转化成什么。
注意到问题是在树上选出一些节点构成一个环。
不妨考虑 dp,设 \(dp(u, x)\) 表示 \(u\) 子树里选 \(x\) 个的方案数。
暴力 dp 是很好做的,我们可以考虑枚举子树里分别选多少个。
可以写出方程 \(dp(u, i + j) = \max\{dp(u, i) + dp(v, j) + 2w(u, v) \times min(k, k - j)\}\)。
后面那部分就是考虑 \(w(u, v)\) 这条边,被下面子树里面的点经过了多少次,会做多少贡献。
注意到这个方程有标准的 \(\max +\) 卷积的形式,可以注意到两边都是上凸壳。
所以我们维护差分转成闵可夫斯基和,并固定 \(i\),考虑 \(j\) 的贡献,然后问题转化为把 \(w\) 那边贡献合并到 \(dp(v, j)\) 上,然后再合并一次就好了。
Gym100739E Life as a Monster §ψ(`∇´)ψ
给定 \(n\) 个整点 \((x_i, y_i)\),支持 \(q\) 次询问。
0 a b c:令 \((x_a, y_a) = (b, c)\)。1 a b:求 \(\sum\limits_{i = 1}^{n}2\max(|x_i - a|, |y_i - b|) + 2(n - 1)\)。强制在线,坐标 \(±10^9\),\(n, q\le 10^5\),TL = 1s, ML = 64MB
最后那一坨东西就是求切比雪夫距离,一堆 max + 堆在一起不好做。
此时有一个经典 trick,切比雪夫转曼哈顿距离(更广义一点的是闵可夫斯基距离)。
比如曼哈顿转切比雪夫,用到的思想就是把 \(|x|\) 写成 \(\max(x, -x)\):
然后考虑合并两个 \(\max\),然后构造 \(|x|\):
所以得到,\((x_1, y_1), (x_2, y_2)\) 之间的曼哈顿距离等于 \((x_1 + y_1, x_1 - y_1), (x_2 + y_2, x_2 - y_2)\) 的切比雪夫距离。
反过来解,可以得到,\((x_1, y_1), (x_2, y_2)\) 之间的切比雪夫距离等于 \((\dfrac{x_1 + y_1}{2}, \dfrac{x_1 - y_1}{2}), (\dfrac{x_2 + y_2}{2},\dfrac{x_2 - y_2}{2})\) 的曼哈顿距离。
然后要求的地方乘了 \(2\),乘法是可以带进绝对值里面的,所以问题转化为求 \((x_1 + y_1, x_1 - y_1), (x_2 + y_2, x_2 - y_2)\) 的曼哈顿距离。
换句话说你现在有一个点 \((a + b, a - b)\),你需要求 \(\sum dis((a + b, a - b), (x_i + y_i, x_i - y_i))\)。
也就是 \(\sum(|a + b - x_i - y_i| + |a - b - x_i + y_i|)\),
(接下来的坐标为变化后的坐标)
因为没有了 \(\max\) 的干扰,我们可以以询问点变化后的点 \((x_0, y_0)\) 为原点分四个半平面出来,分别对每个半平面求一次答案,这就相当于一个二维数点,不过每个点的权值变了下罢了。
式子是 \(\sum(|x_0 - x_i| + |y_0 - y_i|)\)
然后你发现 \(x, y\) 两边独立了,所以其实可以分开做一维数点。
于是现在我们只需要分开维护 \(x, y\),然后对于一个询问,找到这个位置分别做前缀和后缀和就行了。
也就是一个动态一维数点,实际上可以用值域相关的数据结构维护。
但问题在于这里是 64MB,如果是动态开点就寄了,所以我们只能使用平衡树维护了。
CF319E Ping-Pongψ(`∇´)ψ
有一个区间的集合,初始为空。当 \(c<a<d\) 或 \(c<b<d\) ,且 \((a,b),(c,d)\) 都在集合中时,你可以从区间 \((a,b)\) 移动到 \((c,d)\)。你需要支持下面的操作:
1 x y,加入一个新区间 \((x,y)\)。保证加入的区间长度严格单调递增。
2 a b,询问是否能从第 \(a\) 个加入的区间移动到第 \(b\) 个。操作数 \(1\le n\le 10^5\),保证其他任何数字都是整数且不超过 \(10^9\)。
可以注意到连边分两种,一种是包含 -> 单向边。
另一种是相交 -> 双向边,双向边连接后可以直接 Merge 起来,因为题目保证加入的区间长度严格单调递增,所以如果我们把这些由双向边连起来的区间并起来作为代表区间,并不会影响答案,我比较懒就省略了,可以自己画图。
然后可以注意到答案一定不会包含超过一条单向边,因为单向边的关系有传递性,路径一定可以被压缩成一条边。
所以问题有解就是,同处一个连通块,或者具有包含关系。
然后怎么维护加区间操作呢?因为新的区间最大,不会被包含,所以我们就把它们放在线段树上。
对于一个区间,把它拆成 \(\log n\) 个完整的区间,在每个线段树节点上维护一个 vector,然后某个编号的区间被拆成的区间对应的节点的 vector 里就记录以下这个区间编号。
之后考虑从当前区间 \([l, r]\) 的左右两个端点往树根走,路径上的节点的 vector 存的编号就是和当前区间相交的区间,全部弹出和当前区间 Merge 起来。
然后 vector 里只保留当前区间即可(当然更好的实现是先 Merge 完了再放进去)
可以发现,一共 \(n\) 个区间,每个区间会被拆成 \(O(n\log n)\) 个元素放入不同的 vector,每个元素只会进去出来一次,不算上并查集的复杂度,可以做到 \(O(n \log n)\)。
合并的时候还需要维护连通块的左右端点,不然没法判包含。
记得离线之后离散化。
CF1149C Tree Generator™ §ψ(`∇´)ψ
\(n\) 个点,\(m\) 个询问。
给你一棵树的括号序列,输出它的直径。
有 \(m\) 次询问,每次询问表示交换两个括号,输出交换两个括号后的直径(保证每次操作后都为一棵树)
输出共 \(m+1\) 行。
\(3 \le n \le 100\,000,1 \le q \le 100\,000\)
思考一下在括号序列中怎么表达直径。
树的括号序是,往下左括号,往上右括号。
可以发现两点之间的距离可以这样表达:
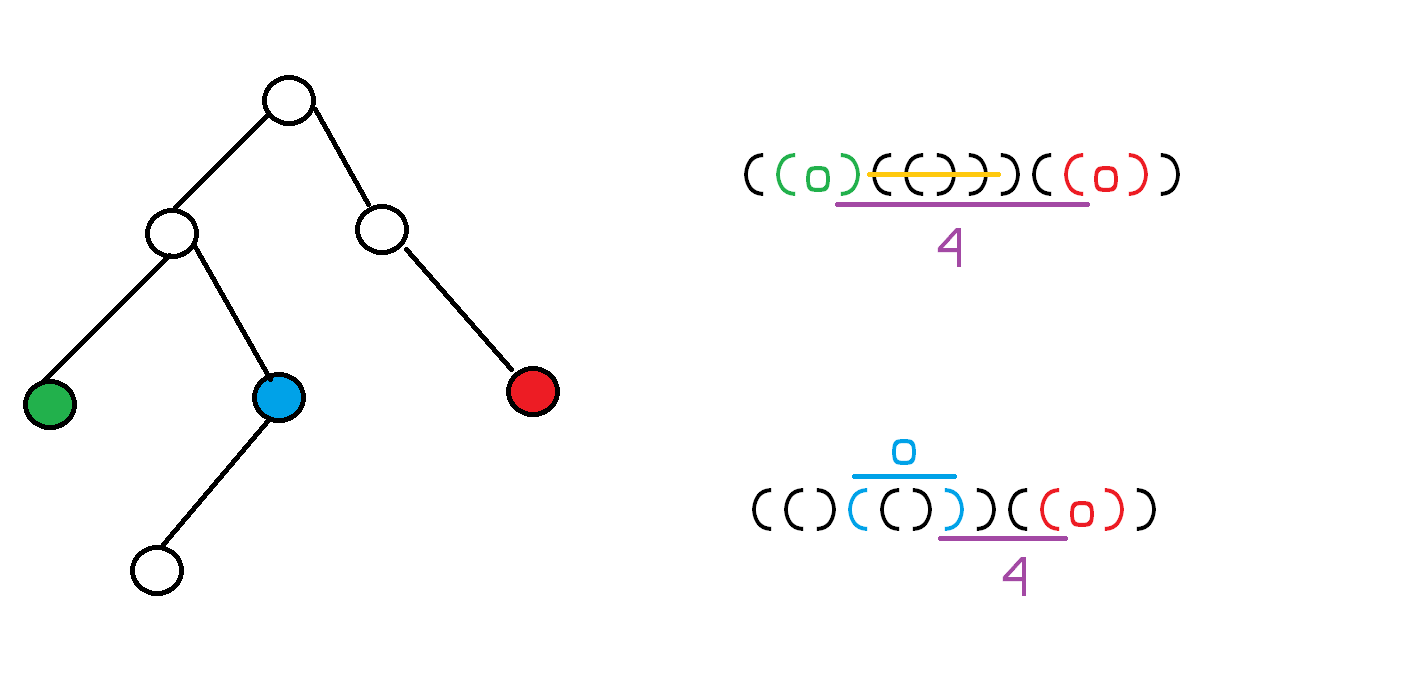
对于一个节点,找到它对应的两个左右括号,删去这中间的括号(肯定是一个合法的括号子串),加入一个点,然后删去这两个点之间的合法括号串,剩下的括号数就是答案,这个还可以加权。
换句话说,对于一对 \((u, v), (dfn(u) < dfn(v))\),那么 \(dis(u, v)\) 就是 \(u\) 的右括号到 \(v\) 的左括号之间,删去所有合法括号串剩下的括号。
这个过程实际上就是考虑怎么从 \(u\) 走到 \(v\) 的,相当于是走出 \(u\),走进 \(v\) 这两条边算一次,然后中间会走过一些子树,把这些子树删掉。
那么直径也就好表达了,不过这也启发我们,一个节点的深度实际上是,记左括号为 \(1\),右括号为 \(-1\),它对应左括号的前缀和。
然后直径就是,任选两个点,使得这个差值最大,这是一个比较类似最大子段和的东西。
现在交换实际上就是单点修改,那么我们考虑直接维护一个区间内的答案,然后通过记录一些信息合并就行了。
应该是要记录区间答案,区间和,最大最小前后缀,之类的,我口胡,哈哈,不写了。
CF264E Roadside Treesψ(`∇´)ψ
在 \(1\sim n\) 的位置能种树,刚开始能种树。
第 \(i\) 个时刻会有操作:
- 在一个没种过树的位置 \(p_i\) 种一颗高度为 \(h_i\) 的树。
- 砍掉第 \(x_i\) 棵树,保证这个位置以后不会种树。
每天树会长高 \(1\)
每执行一次操作,输出最长上升子序列长度
任意时刻树的高度不同
Translated by@Fheiwn(吐槽一下你行内数学公式写的好鬼畜)
\(1\le n\le 10^5, 1\le m \le 2\times 10^5, 1 \le h_i,x_i \le 10\)。
你知道吗我第一眼看这题我想的 ddp /tx
然后就发现这个数据范围不太对劲,似乎可以有更简单的维护方式。
看到这个 \(10\) 我们想到,可以暴力搞这一部分,但是这样的话就会更新后面的,所以我们倒过来,让它们在末尾,求一个下降就行了。
然后插入也只需要算十颗树就行了,时间这个减一减弄掉,应该随便拿个什么数据结构维护一下就好了。
CF226E Noble Knight's Pathψ(`∇´)ψ
shaber 题,除了代码实现没有任何难度,不花时间了。
HDU7144 Treasureψ(`∇´)ψ
ZOJ2674 Strange Limitψ(`∇´)ψ
CF687B Remainders Gameψ(`∇´)ψ
HDU6265 Master of Phiψ(`∇´)ψ
POJ3910 GCD Determinantψ(`∇´)ψ
Voyager1ψ(`∇´)ψ
矩阵游戏ψ(`∇´)ψ
Power Towerψ(`∇´)ψ
Borderψ(`∇´)ψ
[NOI2016] 网格ψ(`∇´)ψ
给定 \(n \times m\) 的网格,其中 \(c\) 个格子是黑色的,其余格子都是白色。
称两个白色格子是连通的,当且仅当这两个白色格子相邻(四连通)或存在另外一个白色格子与这两个格子连通。
问至少要将多少个白色的格子染成黑色,使得至少存在两个白色格子不连通。
\(1\le T \le 20, 1\le n,m \le10^9, \sum c \le 10^5\)。
观察到答案上界为 \(2\),也就是考虑角上(咦,我之前是不是开过一个答案上界很小的专题,似乎有这个玩意儿),类似围棋。
注意到要至少两个白格子不连通,而 \(nm = 1\) 是可能的,所以有可能无解。
然后如果已经有被围住的,答案为 \(0\),如果是围着只剩一口气,那么答案就是 \(1\)。
否则答案就是 \(2\)。
然后这样判起来还是有点麻烦,我们注意到黑点数量不多,考虑从这个入手。
如果存在一个闭合的黑点连通块且不是围住了边框,答案为 \(0\)。
然后如果存在一个黑点连通块,使得它们差一个黑点就连通了,答案为 \(1\)。
其他时候答案为 \(2\)。
第二个情况还是不好做,怎么办怎么办?????
好像只能考虑白点了,先忽略点数级别问题。
第二个情况就是,原图存在割点。
然后看看能不能,忽略一些点(常见套路)。
注意到其实只有和黑色格子挨着的的才有用,其它的肯定都连通了,我们只关心被我们提取出来的节点的连通性。
我们就把这些白格子提取出来,点数就只有 \(O(C)\) 级别了。
首先判无解,然后 BFS 判是不是已经不连通了,再考虑是否有割点,做完了……吗?
好然后你就咍咍了,我们考虑这样一个情况:
1 2 3 | |
其中 X 为黑点,* 和 O 分别为被选出的白点和其他白点,如果我们只考虑八连通,H 就会被计算成割点。
原本答案是 \(2\),现在答案变成了 \(1\),GG,所以应该处理二十四连通。
好然后你又寄了,如果我说,你算出来的割点周围可能没有黑点,阁下又将如何应对?
1 2 3 4 5 | |
咍咍,所以割点的周围四连通的格子中必须要有黑点。
写起来估计有点麻烦,所以要写这个题。
所以应当怎么规避,或者说怎么才能一次想到这样的特例!!
特别是有毒瘤出题人给极弱大样例的时候,怎么办!!!!
CF19E Fairy §ψ(`∇´)ψ
给定 \(n\) 个点 \(m\) 条边的无向图。对于每条边,询问删去这条边之后剩下的图是否是二分图。
\(1\le n, m \le 10^4\)。
满足条件的边一定是所有奇环的并,没有奇环就是都可以删。
无脑做法:并查集维护二分图是大家都会的,拆点之后按照 \((u, v + n), (u + n, v)\) 连边,如果 \(u\) 和它自己联通了那就是奇环了。
然后我们可以分治考虑这个过程,考虑加入 \([mid + 1, m]\) 这些边,递归处理 \([1, mid]\) 的边。
直到叶子节点,判一下,然后用一个可撤销并查集就行了。
长脑子做法:图是坏的,我们考虑 dfs 树,这是处理无向图最有力的工具之一!
我们考虑把图中所有环转化成一条非树边 \((u, v)\) 以及 \(\delta(u, v)\) 构成的整体。
可以发现这一定覆盖了图中所有环,证明很简单,不妨假设有一个两条边组成的环,它其实可以被看作两个这样的环的并。
并的方式是,把边的出现次数异或起来,如果还是 \(1\),那么新环上就还有这条边。
然后我们考虑一个奇环是怎么生成的,显然是,本身就是一个奇环,或者是奇环和偶环的并。
考虑答案边应当具有什么样的性质。
对于一条能够连出奇环的非树边,我们称它是恶毒的。
可以注意到答案边一定会和所有恶毒边存在于同一个环上,我们不妨利用恶毒边来计数。
另一个性质是,非恶毒边一定不会和答案边共处一个环上。
这是显然的,因为偶环和奇环的并是一个奇环,答案边一定只能存在于奇环上。
我们考虑一个偶环和奇环的并是什么样的:
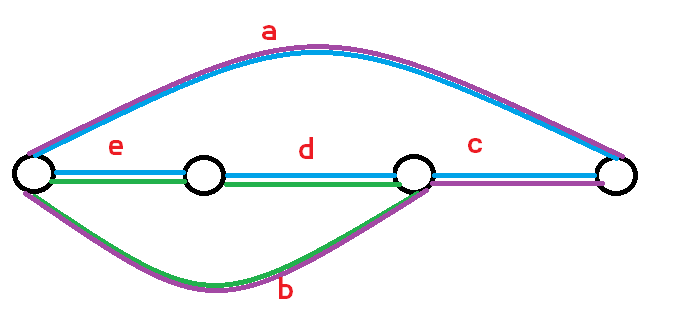
恶毒边是 \(b\),非恶毒边是 \(a\)。
显然答案边只能是环 \((b,d,e)\) 和环 \((a,c,b)\) 的交即 \(b\),不过它不是树边,计数的时候不用关心,最后算一下就好。
\(a\) 在原树上构成的环为 \((a,c,d,e)\) 不包含 \(b\)。
其它的拓展归纳可以证明。
进一步可以证明,一个树边是答案边,当且仅当它满足以上两个条件。
于是树上差分统计一下即可。
可能需要复习下树上差分和可撤销并查集,写不写看心情。
HDU5582 Journey of Takuψ(`∇´)ψ
给定 \(N\) 个点 \(M\) 条边的带权无向图,要从点 \(1\) 走到 \(N\)。
在点 \(x\) 时,可以走一步移动到 \(x\) 的邻居。有两种移动方式:
令 \(px\) 为走到 \(x\) 的上一步,\(w\) 为从 \(px\) 走到 \(x\) 的边权。令 \(y1, y2, \dots, yk\) 为 \(x\) 所有除了 \(px\) 的邻居。那么 \(x\) 会走到所有 \(y\) 中边权和 \(w\) 最接近的 \(y\)。如果这样的 \(y\) 有多个,选择编号最小的 \(y\)。如果 \(x\) 不存在除了 \(px\) 之外的邻居,就走回 \(px\)。
任意选择 \(x\) 的邻居并移动过去
第一种移动方式可以任意使用,而第二种移动方式必须要在连续使用至少 \(K\) 次方式一之后才能使用。问从 \(1\) 走到 \(N\) 的最小步数。
\(1\le n,m,k \le 10^5\)。
可以很显式的注意到,如果我们从某个点开始,假设只走第一种操作,能到达的位置是固定的。
这个可以倍增处理,不过要记得倍增的时候处理的是边,就是说,从某条边开始走,下一步去到的“边” 是确定的,然后倍增可以求出第 \(K\) 步去到哪个边。
然后第二个操作这个限制,我们可以强制让 Taku 走 \(K\) 步,然后连边。
具体来说我们拆点考虑分层图,第一层对边建点,然后它连向第二层的某个点(也对应一条边)满足这个点对应的边是第一层那个点对应边走 \(K\) 步到达的边。
然后第二层的边就可以随便连向第一层中它在原图上用第二种方式能去到的边对应的点,相当于第二种移动。
当然我们这里是至少 \(K\) 步,所以如果我们到达了这个节点,并不是说我们就一定要用第二种移动方式,还可以继续用第一种移动方式,这个部分因为第一种移动的确定性,直接连向第二层中那条边对应的节点就行了。
但是还有一个问题,第一层往第二层连边是唯一确定的,第二层往第一层连边可能有很多后继,这样会被卡掉,但是这里会重复使用。
所以我们不妨开第三层,第三层是原图节点,然后第二层往第一层连边就通过第三层中转一下就好。
注意一下连边的边权,跑一次 Dij 最短路就好了,可能倍增的时候需要注意一下。
应该会写吧,或者会选择看懂别人的 Ac 代码。
ATC keyence2019 E Connecting Citesψ(`∇´)ψ
给定 \(N\) 个点的完全图,每个点有权值 \(A_i\)。
对于任何点 \(i\) 和点 \(j\),这两点之间的边权为 \(w_{i,j} = A_i + A_j + D|i − j|\)。其中 \(D\) 为给定的常数。
求最小生成树的大小。
\(1\le n \le 2\times 10^5, A_i, D \le 10^9\)。
可以从 Prim 和 Kruskal 两个角度入手,我不咋会 Prim 就考虑 Kruskal 了。
分离变量,记 \(S_i = A_i - Di, T_i = A_i + Di\)。
很容易想到,\(O(n^2)\) 条边应该只有很少一部分边是有用的。
也就是说我们希望删去大部分,删去后对于 MST 没有影响的边。
有一个想法是对于一个 \(i\) 我们只保留它两侧最优的两条边,这个 bit 维护一下就好了。
但是这样一定能保证原图还联通吗,好像是可以的但是我不会证明?
没脑子做法:可以类似 CDQ 分治,连边只连跨越两部分的边当中的边。
但是这东西我不知道怎么证明原图还是联通的,所以我不写。
CF266D BerDonaldsψ(`∇´)ψ
给定 \(n\) 个节点 \(m\) 条边的无向图,第 \(i\) 条边有长度 \(w_i\)。
需要找到一个点(不一定是某个节点之一,可以在某一条边上),使得这 \(,n\) 个节点到这个点的最大距离尽可能小。
\(1\le n \le 200, m \le \dfrac{n(n - 1)}{2}\)。
shaber 题吧,注意到一定在 \(1, 0.5\) 的位置,可以转成整数。
无脑做法是 Floyd 之后三分位置,因为这个是单峰的。
但是三分是实数,坏,听说会被卡。
长脑子做法:边拆点不现实,数据范围不允许。
然后如果我们把所有边相关的单峰函数凑到一起,就是一堆局部单峰的,长这样的玩意儿:
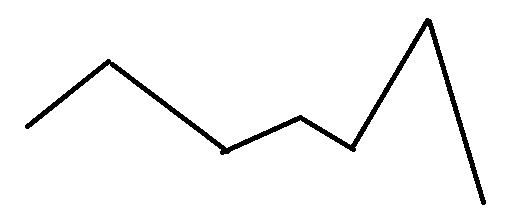
合并之前的我没画,但是可以知道所有交点当中最优的就是答案。
直接暴力不太行,可以排序固定一个暴力扫,复杂度 \(O(n^3 + n^2\log n)\)。
具体的东西有时间再来画,反正是 shaber 题就对了。
CF555E Case of Computer Networkψ(`∇´)ψ
给定 \(n\) 个点 \(m\) 条边的无向图以及 \(q\) 个点对 \(s_i,t_i\)。要求给每条边定向使得对于每个 \(i\),都存在一条有向路径从 \(s_i\) 走到 \(t_i\)。
问是否存在这样的方案。
\(1\le n, m, q \le 2\times 10^5\)。
这不是 shaber 题吗,怎么还是 d1E。
缩边双,边双连通分量内的一定存在构造方式。
然后转化为一个树上差分的形式,看看是不是存在一条边被定向成两个方向了。
这个两次树上差分就能做。
Bonus: 构造方案。
这个也是 Trivial 的,点双内部只需要找到一个环,然后不断把没在环上通过加“同方向的链”的形式加进来就行,实现可能不太好搞。
类似这样,比较像耳分解的形式:
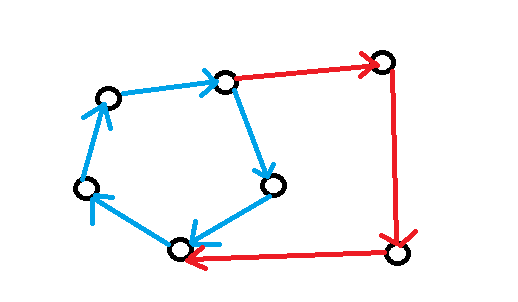
shaber 题就不写了。
CF639F Bear and Chemistryψ(`∇´)ψ
小 t 没场切的题,有天赋哥 5s 秒了 😱
给定一张 \(n\) 个点 \(m\) 条边的初始无向图。
\(q\) 次询问,每次询问给定一个点集 \(V\) 和边集 \(E\)。
你需要判断,将 \(E\) 中的边加入初始无向图之后,\(V\) 中任意两个点 \(x,y\) 是否都能在每条边至多经过一次的情况下从 \(x\) 到 \(y\) 再回到 \(x\)。
\(n,m,q,\sum |V|, \sum |E| \le 3 \times 10^5\),强制在线。
以一种比较奇怪的方式强制在线,具体看题面。
好像是 shaber 题。
边双嘛,这个太显然了。
如果在边双里面的,不管怎么加都可以,所以直接缩点,问题转化为树上。
然后注意到对于给定的点集,我们其实只关系他们的“连通性”,我们并不在乎它们的实际位置。
所以我们可以把这些点拖出来建虚树,然后加边,再缩点,就可以了。
因为很显然虚树并不影响连通性,然后就没了,巨大难写,还是写一下。
CF878C Tournamentψ(`∇´)ψ
shaber 题。
最近Berland开始了一场有 \(k\) 种运动的比赛。瓦萨亚希望在赌场上赚钱。 比赛的计划非常神秘,并没有完全公开。比赛选手背靠背举行,每场比赛都涉及两名尚未淘汰的运动员。每场比赛都可以举行 \(k\) 种运动里的任意一种,失败者则遭到淘汰。最后剩下的运动员成为冠军。除此之外,该方案可以是任意的,不提前公开。 瓦西亚了解各种运动中的运动员的力量。他认为,拥有更高力量的运动员总能获胜。 比赛每年举行一次,每年都有一名新参赛者加入比赛。在第一场比赛中,只有一名运动员参加,第二场比赛有两名运动员,依此类推。 请你帮助他找到 \(n\) 年每一年可能获得冠军的人数。
\(1\le n \le 5\times 10^4, 1\le k \le 10\)。
把是否能赢转化为有向边,缩点,可以发现这一定是一条链。
然后第一个 SCC 大小就是答案,不懂这种 shaber 题。
yi?等下,这是动态加点,完,我是 shaber,考虑下怎么做。
可以使用 set 维护,能合并就是,有相互可以赢的项目,然后可以把这个条件重载为 set 的小于号,每次 find 一下就可以找到能合并的。
答案是 set 中“最大”的元素。
CF76A Giftψ(`∇´)ψ
有一个国家有 \(N\) 个城市和 \(M\) 条道路,这些道路可能连接相同的城市,也有可能两个城市之间有多条道路。
有一天,有一伙强盗占领了这个国家的所有的道路。他们要求国王献给他们礼物,进而根据礼物的多少而放弃占领某些边。对于每一条道路,强盗都给出了相应的要求,金子 \(g_i\) 的数量,银子 \(s_i\) 的数量。也就是说若国王给强盗 \(G\) 个金子,\(S\) 个银子,那么他们就会放弃占领满足 \(g_i\le G \land s_i\le S\) 的道路。
现在国王知道金子、银子的单价,他想花费钱财购买金银送给强盗,使强盗放弃一些道路,进而使N个城市能互相到达。但是国王又想花费最少。请你计算最少的花费
\(N\le200,M\le50000\)
没啥好做法拆分维护信息,暴力枚举一维转成普通 MST,复杂度 \(O(M^2)\)。
然后考虑优化,设当前可选的边的集合为 \(A\),选中的边的集合为 \(B\),也就是说 \(B\) 是当前最优的边。如果后面枚举金子数时加进来新的边,那新的生成树的边肯定也是在新边和 \(B\) 集合中找。也就是说,\(B\) 在 \(A\) 中的补集已经没有用了1。
所以每次只需要维护 \(n\) 条边,复杂度降为 \(O(NM)\)。
JOI 2018 Final 月票购买ψ(`∇´)ψ
给定 \(N\) 个点 \(M\) 条边的带权有向图,和四个点 \(X,Y,U,V\)。
选择一条从 \(U\) 到 \(V\) 的最短路并将权值设为 \(0\),并最小化修改后 \(X\) 到 \(Y\) 的最短路。
\(n \le 10^5, m \le 2\times 10^5\)。
神秘题,感觉一个显然的事情是我们希望 \(u\to v\) 的最短路经过 \(x \to y\) 的某条路径使得它变短。
不然你咋做。
呃呃,然后我不咋会了,想一想。
哦哦,首先重叠的是一段,并且只有一段,记为 \(s \to t\)。
答案是求 \(\min\{dis(x, s) + dst(t, y)\}\),现在的问题是怎么保证这个路径的合法性。
对 \(u,v,x,y\) 分别跑一次最短路,方便处理。
然后注意到其实可以求出 \(u\to v\) 的一个叫最短路 DAG 的东西,这个上面就是可以变成免费的路径。
然后问题就可以直接 dp,分别算 \(dis(x, s)\) 和 \(dis(t, y)\),在路径上随便怎么询问一下应该就可以了。
具体的可能还需要想想。
TCO17 Final HiddenRabbitsψ(`∇´)ψ
咋想到 2-SAT 的啊,不太懂,当然有可能是我 2-SAT 题做少了。
给定 \(n\) 个点的无根树,常数 \(m\) 和 \(k\) 条限制。需要找到一个合法的序列 \(h_0, h_1, \dots, h_{m-1}\) 满足以下条件:
\(h_i \in [0, n - 1]\)
对于第 \(i\) 条限制,要求在以 \(r_i\) 为根时 \(h_{x_i}\) 和 \(h_{y_i}\) 的最近公共祖先为 \(z_i\)。
\(n, m, k \le 250\)。
考虑记 \(S(u, v)\) 表示命题:\(u\) 在以 \(v\) 为根的子树内。
然后尝试把所有情况都用这个命题描述,记得逆否命题。
对于原图处理完之后再对于限制考虑,应该就是这样。
BZOJ1950 Linkψ(`∇´)ψ
给定一个 \(N\) 个点 \(N\) 条边的有向图(内向树), 要求在图上添加最上的边,使得点 \(1\) 到达所有其他点的最短路长度不超过 \(K\)。
\(2\le N \le 5e5, 1\le K \le 2e4\)。
基环树处理方式不多,但大多都基于一个思想,就是环和树分开考虑。
不妨先考虑树的情况,可以发现因为这是一颗内向树提出来的树,所以叶子节点是没法从 \(1\) 到达的,除非 \(1\) 就是叶子。
然后我们考虑连向所有叶子,然后往上不停的找距离超过 \(K\) 的点,连边继续向上跳。
然后对于一棵树,显然他跳到环上的时候可能有空余,标记环上节点。
问题转化为在环上有一些节点被标记了,有些没有被标记。
现在需要加最少的边让它们都被标记,没啥好办法,考虑枚举没有被标记的点,为了最优一定选 \(dist = k + 1\) 的,然后每次暴力往后扫标记。
然后关键点最多 \(k\) 个,这部分是 \(O(kL)\),\(L\) 是环长。
这样暴力是坏的,因为我们实际上是在覆盖,不妨考虑差分,可以除以一个 \(k\)。
整体复杂度 \(O(N)\)。
细节应该是要考虑 \(1\) 的位置单独处理。
CF1137C Museums Tourψ(`∇´)ψ
一个国家有 \(n\) 个城市,通过 \(m\) 条单向道路相连。有趣的是,在这个国家,每周有 \(d\) 天,并且每个城市恰好有一个博物馆。
已知每个博物馆一周的营业情况(开门或关门)和 \(m\) 条单向道路,由于道路的设计,每条道路都需要恰好一个晚上的时间通过。你需要设计一条旅游路线,使得从首都:\(1\) 号城市开始,并且当天是本周的第一天。每天白天,如果当前城市的博物馆开着门,旅行者可以进入博物馆参观展览,否则什么也做不了,这一天的晚上,旅行者要么结束行程,要么通过一条道路前往下一个城市。当然,旅行者可以多次经过一个城市。
要求让旅行者能够参观的不同博物馆数量尽量多(同一个城市的博物馆参观多次仅算一次),请你求出这个最大值。
\(1\le n\le 100,000\),\(0\le m\le 100,000\),\(1\le d\le 50\)
这种多状态一看就是分层图。
又发现 \(d\) 很小,莽!
就是按照天往后连边,然后可以跑一个点权最长路。
但是有环,比较烦,注意到是有向的,所以 Tarjan 一下,SCC 点权是里面本质不同博物馆的个数。
这个暴力算就行。
shaber 题不写了。
CF1155F Delivery Oligopoly §§ψ(`∇´)ψ
给定一张 \(n\) 个点 \(m\) 条边无向图 保证它是一个边双连通分量
你需要求出它的一个包含 \(n\) 个点的子图 满足两个条件:
- 这个子图必须也是边双连通分量
- 这个子图的边数最少
数据保证有解,你需要输出这个子图的所有边
\(3 \le n \le 14, n \le m \le \dfrac{n(n - 1)}{2}\)
趣味题。
状压状压状压。
设 \(dp(msk)\) 表示 \(msk\) 集合内的点组成边双的最小边数。
但是我们没法转移,因为边双的子集不一定为边双,不然这题出出来是干嘛的。
思考一下没法转移的原因,因为我们不知道从 \(msk\) 能转移到哪里,或是从哪里来。
然后我们想到一个神奇的充要条件,我记得以前和柚子讨论那个被毙掉的 Div1F 超级无敌炫酷牛逼最后 Open 的题的时候了解到过耳分解和双极定向,也提到了这个结论。
无向图有耳分解当且仅当它是边双连通的。
这是充要条件,反过来是一样的,所以我们考虑从这个地方切入,尝试找到耳,然后转移。
缩小是难做的,尝试扩展,那么每次我们尝试构造一个耳来扩展边双。
可以枚举 \(msk\) 当中的两个点,然后构造一个最短的,除了 \(u, v\) 以外,没有节点在 \(msk\) 中的链,这个链是可以预处理的。
转移就是 Trivial 的了,需要记录转移路径。
比较好写,可能会看看。
补充:有向图对应的条件是强连通。
麻了被 cftm 和小怪兽还有 45dino 怒斥了/ll
UOJ37 [清华集训2014]主旋律 §§ψ(`∇´)ψ
给定 \(n\) 个点 \(m\) 条边的有向强连通图,问有多少边的子集删去之后图仍然强连通,答案对 \(10^9 + 7\) 取模。
\(1\le n \le 15, m \le n(n - 1)\)。
这题咋感觉和上一题那么像啊,都是神仙题。
问题也出在状压没法转移上面,但是完全没有思路啊,好难啊,我最后来写好了。
UOJ465 [HNOI2019] 校园旅行 §§ψ(`∇´)ψ
我草 500 万年前乱翻博客翻到过这个题出题人的博客,记得还说 pdf 印刷错误了。
怎么是你啊,Tour,究极神题。
某学校的每个建筑都有一个独特的编号。一天你在校园里无聊,决定在校园内随意地漫步。
你已经在校园里呆过一段时间,对校园内每个建筑的编号非常熟悉,于是你情不自禁的把周围每个建筑的编号都记了下来——但其实你没有真的记下来,而是把每个建筑的编号除以 2 取余数得到 0 或 1,作为该建筑的标记,多个建筑物的标记连在一起形成一个 01 串。
你对这个串很感兴趣,尤其是对于这个串是回文串的情况,于是你决定研究这个问题。
学校可以看成一张图,建筑是图中的顶点,而某些顶点之间存在无向边。对于每个顶点我们有一个标记(0 或者 1)。每次你会选择图中两个顶点,你想知道这两个顶点之间是否存在一条路径使得路上经过的点的标记形成一个回文串。
一个回文串是一个字符串使得它逆序之后形成的字符串和它自己相同,比如“010”,“1001”都是回文串,而“01”,“110”不是。注意长度为 1 的串总是回文串,因此如果询问的两个顶点相同,这样的路径总是存在。此外注意,经过的路径不一定为简单路径,也就是说每条边每个顶点都可以经过任意多次。
\(1\le n \le 5e3, 1\le m \le 5e5, 1\le q \le 1e5\)。
暴力的 dp 是好想的,设 \(dp(u, v)\) 表示 \(u \to v\) 是否可行。
然后这个可以首先把本来就是回文串的(\(len = 1, 2\))的情况标记,然后枚举 \(u, v\) 的同色出边扩展,一个 BFS 就行了。
复杂度 \(O(m^2)\),做不了一点,但我们注意到 \(n\) 的范围很有猫腻,感觉是不是可以做到复杂度和 \(n\) 相关!
于是现在有两种想法,一种是对 dp 重新设计状态,但是这是显然不行的,我们没法以更优秀的形式覆盖整个状态空间了。
所以只剩下一种办法,考虑去掉一些,没有用的边。
那么,怎么样的边才是没用的呢?很好我不知道,还是看看远方的题解吧家人们。
人类智慧想法是对转移分类,一类是同色边转移,一类是不同色边转移。
先考虑同色边,这在原图上划分出了若干个连通块,考虑每个连通块对转移做的贡献。
可以注意到因为能够重复走,我们希望整合,连通块中所有的 \(\delta(u, v)\) 的长度,变成一条单一的 \(\delta(u, v)\),长度不够可以靠重复来凑,因为我们只关心判定问题,不关心具体值,所以长度长了和长度不够是等价的,但是要能整合,就说明它们满足一些共同的性质。
可以注意到,如果连通块是二分图,那么 \(\forall \delta(u, v)\) 的奇偶性是相同的,这个考虑二分图形态即可。
那么我们不妨直接只保留一条 \(\delta(u, v)\),因为奇偶性相同嘛,最终的体现就是一颗生成树。
然后不是二分图怎么办?很简单,随便拉一个点加个自环,这样不同奇偶性的路径可以通过走一次自环来整合。
至于不同色,它本身就是二分图,所以保留生成树即可。
那么现在会剩下多少边呢?对于一个连通块,我们保留的是生成树,所以对于连通块,边数是 \(O(n)\) 的,极端一点的情况下,显然边数也和点数相关。
所以最后实际有用的边只有 \(O(n)\) 条,复杂度 \(O(n^2)\)。
我草,这题太牛逼了。
Codechef TAPAIR Count The Important Pairs §§ψ(`∇´)ψ
怎么还有正解随机化的 shaber 题,fun。
给一张 \(n\) 点 \(m\) 边的无向连通图,求有多少对 \((i, j)\) (无序)使得切掉 \(i, j\) 两条边之后图不连通。
\(1\le n \le 10^5, 1\le m \le 3\times 10^5\)。
边三连通分量,真有你的,CodeChef.
桥可以和所有边做贡献,这个统计一下桥边数量即可。
考虑对于连通块(边双)做计算,我们只需要考虑让连通块内部断开的方案。
然后这里经典的考虑 Tarjan 的 dfs 树并进一步做贡献。
所有非树边不是返祖边就是横叉边,删两条返祖边/横叉边/各删一个是没有用的,因为有树在,所以我们至少要断掉一个树边。
考虑删树边,就两种情况,一种是我们断掉了一条树边,然后下边的子树往外的横叉边或者返祖边就一条,删掉这个就行了。
另一种是删了两个树边,这说明被弄出来靠下的两个子树都没有向上的返祖或者横叉边,它们之间有连边是无所谓的。
这个好像很难处理,别急,想想咋做,把人类语言转化为条件。
先考虑最后一个吧,这条件说明了什么呢?
换个角度考虑,既然这两条边删去之后可以使得原图不连通。
那么也就是说,删去其中一条之后,另外一条变成了桥边,这说明什么,这说明被删去的边断掉了之后,没有环能够覆盖另一条。
这说明两条边被环覆盖的情况是一致的,意思是对于某条非树边,它加到 dfs 树上之后可能有很多环,对于同一条非树边,这两条被选中的边应该在同一个环上。
所以问题转化为对于一个非树边构成的环,我们需要标记边(有点类似 CF19E Fairy 那个的感觉)。
第一种情况类似,可以发现如果某条路径只被某一条非树边覆盖了,那么删去非树边之后这条路径上任选一条都可以。
那么怎么判断覆盖情况是否相等呢?开一个 set 记录?不现实。
好然后我们就要开始随机了,给每个非树边赋一个不同的,ull 范围内的随机权值。
然后覆盖了就直接用树上差分维护异或和,两个边的异或和相同证明被覆盖的情况相同。
然后把树边拖下来按照异或和分组,分别考虑计算即可。
这种 Hash 的思想上面的 New Year and Conference 也有用到,很好玩。
大概就是,利用 Hash 或者随机化优化集合之间的比较!
Gym102770L List of Productsψ(`∇´)ψ
定义两个数的比较方式是唯一分解后,从小到大枚举质因子 \(p_i\),\(e_i\) 小的更小,比如说 \(30 < 4\)。
给你两个序列 \(a, b\),问两两相乘后第 \(k\) 大是多少。
\(1\le n\le 10^5, a_i, b_j \le 10^6\)。
首先这个比较感觉上来说是没法优化的,最快也就 \(O(\sqrt V)\) 比较两个数。
Gym102769L Lost Templeψ(`∇´)ψ
给你一个 \(n\) 列的网格图,每一列 \([l_i,r_i]\) 有点,每天会把最外层的点删掉,问每列被删完的时间。
\(1\le n \le 5\times 10^6\)。
Gym102769I Intestellar Hunterψ(`∇´)ψ
你每次可以获得一个技能 (a, b),表示可以走 (a, b) 或 (−a, −b),每次
问一个点能不能用你已有的技能组合从 (0, 0) 走到,坐标是非负的。
\(1\le q \le 10^5\)
如果这个题是一维的就很简单了,可以发现这就是一些数的线性组合,能到达的就是 \(\gcd\) 能到达的。
那么考虑如何扩展成二维,好像 Bezout 并没有二维形式,所以我们考虑,把影响转成一维的。
考虑到答案实际上是多个向量的线性组合,我们不妨分解向量,找到一组基底。
具体怎么选呢?根据平面向量基本定理,只要两个基向量不共线,任意一个向量的分解是唯一的,所以我们怎么方便怎么选。
垂直分解有概率分解不出整数倍数。
不妨分解为 \(\{(a, 0), (b, c)\}\) 的形式,每次加入一个向量 \((x, y)\),我们就让它和 \((b, c)\) 组合,然后再分解到 \(x\) 轴上,具体来说合成的向量在 \(x\) 轴上的投影为 \(d\),那么新的 \((a, 0)\) 就变成了 \((\gcd(a, d), 0)\)。
\((b, c)\) 的话,\(b\) 这边不用管,贡献已经被另一个向量算了,更新 \(c\) 即可。
但是我不知道咋证明,这啥啊,没搞懂,不会证。
Gym102586A Cookies §§ψ(`∇´)ψ
给一个序列 \(a_i\),和一个序列 \(b_j\) 以及操作序列 \(S_j\),对每个 \(k \in [1, n]\) 求出下面过程后的答案:
一开始有一个集合 \(a_1,\dots a_k\),然后从 \(1 \to m\) 开始扫,每次插入 \(b_j\),然后根据 \(S_j\) 弹出最小值或最大值。
问最后剩下的数的和是多少。
\(1\le n,m \le 2e5, V = [0, 10^9]\)。
非常炫酷题目,爱来自 Enonya。
看到这个对于所有 \(k\),老生常谈了,肯定知道我们是要做继承,考虑从上一阶段到这一阶段的贡献。
因为删去的数的个数是固定的,所以当 \(k\gets k + 1\) 的时候,剩下的数的个数也只会 \(+1\)。
那么我们考虑最后多出来的这个数是什么,假设我们已经完成了上一个阶段的所有操作,现在新增了一个数 \(a_k\)。
我们考虑继续扫过去,每次看一下上一阶段被弹出的值 \(c\) 是啥,如果 \(a_k\) 相对于它,更应该被弹出,我们就 \(\text{swap}(a_k, c)\),不断这样做,然后就能知道最后新增了哪个数了。
但是这样和每次都重构一边没有区别,复杂度都是平方的。
这时候不然考虑优化不然考虑 remake,都试试。
考虑优化,注意到操作序列中连续的一段对应的操作是可以整体处理的,比如说有一段都是在弹出最小值,我们不妨维护一个堆,求出这一段中被弹出的所有数的最大值,这说明上一阶段中这一段只留下了这一个数,我们只需要比较 \(a_k\) 和这个值的关系即可。
但是这样还是不咋优秀,有点 ODT 颜色段均摊的感觉,反正很好卡,还是平方的。
此时炫酷 ad-hoc 结论出现了,我们注意到,如果有一个弹出最大值的段 $ A$,它弹出的所有最大值的最小值比它右边的一个弹出最小值的段 \(B\) 弹出的最小值的最大值还大,那么 \(A\) 对 \(B\) 是没有影响的。
换句话说,我们可以交换 \(A,B\),仍然不改变问题的答案。
那么我们能就可以通过选择性的交换,造出新的段,这个用可并堆维护一下就好。
复杂度:我不会证,C 的 FSYo 的。
我们定义势能为相邻两个对反序的个数,即后面的比最大堆的 \(\min\) 大的个数那么每次操作后相邻对的势能必定减 1,每个势能会贡献 1 次,减为 0 就合并了,故复杂度为 \(O(n \log n)\)
很趣味啊,我不想胡了,先写写这个。
Gym102538H Horrible Cyclesψ(`∇´)ψ
Gym102538C Cells Blockingψ(`∇´)ψ
Gym102331H Honorable Mentionψ(`∇´)ψ
Gym102331F Fast Spanning Treeψ(`∇´)ψ
CF1270I Xor on Figuresψ(`∇´)ψ
CF1408H Rainbow Triplesψ(`∇´)ψ
USACO 20Dec Platinum Cowmistryψ(`∇´)ψ
[NOI2014] 动物园ψ(`∇´)ψ
求一个数组 \(num(i)\) 表示,\(s[1...i]\) 的子串中的“变种” border 的个数。
变种 border 是指,在原来 border 前后缀相等的前提下,前后缀不重合的前缀。
\(T\le 5, 1\le n \le 10^6\)。
BZOJ1461 字符串的匹配ψ(`∇´)ψ
定义 \(a, b\) 两个序列相同,当且仅当它们离散化过后相同。
在此语境下,求 \(b\) 在 \(a\) 中那些位置出现了。
感觉是送分题,我们不妨考虑 KMP 的过程,就是在字符“不相等”的时候失配。
注意到这里定义了相等,自然也定义了不相等,我们考虑描述这个相等。
可以发现离散化过后相同当且仅当它们前面比它小的数的个数相同。
于是我们树状数组维护一下就好了。
BZOJ1535 Sza-Templateψ(`∇´)ψ
给一个串 \(s\),你要求出一个串 \(t\) 使得它能通过盖章的方式生成原串。
可以重合,但是不能是不同字符重合,重合后必须是相同的。
\(1\le n \le 10^6\),求\(\min\{|t|\}\)。
注意到 \(t\) 一定是 \(s\) 的一个 border。
并且要满足 \(t\) 的所有出现位置重叠能覆盖完 \(s\)。
可以注意到一个前缀的所有出现位置等价于 Fail 树上它的所有子节点。
所以我们保证子节点排序过后,它们之间的 gap 不超过当前前缀的长度就行。
但是注意到加入这个是不好做的,所以我们直接删,因为 border 在 Fail 树上一定在 \(s\) 的祖先集合中,所以答案是在一条 \(len(s)\) 到根节点的链上的,那么从根节点删下去就行,用一个 set 维护就好了。
BZOJ2061 Countryψ(`∇´)ψ
BZOJ4231 回忆树ψ(`∇´)ψ
[NOI2011] 阿狸的打字机ψ(`∇´)ψ
CCPC Final 2022 Bψ(`∇´)ψ
CF1801G A task for substringsψ(`∇´)ψ
[HAOI2017] 字符串ψ(`∇´)ψ
注意到问题可以转化为, \(p_i\) 当中有 \(k\) 个可以通配。
那么我们发现可以匹配的是一个前后缀。
所以我们对 \(p_i\) 正反都建一次 AC 自动机,问题转化为在 Fail 树上做统计。
是一个要去重的二维数点,之后来胡。
CF914F Substrings in a Stringψ(`∇´)ψ
模拟赛考过的原题,bitset 维护即可。
BZOJ4310 跳蚤ψ(`∇´)ψ
[HEOI2016/TJOI2016] 字符串ψ(`∇´)ψ
[NOI2016] 优秀的拆分ψ(`∇´)ψ
[BJOI2020] 封印ψ(`∇´)ψ
[NOI2015] 品酒大会ψ(`∇´)ψ
[AHOI2013] 差异ψ(`∇´)ψ
CF713D Animals and Puzzleψ(`∇´)ψ
CF677D Vanya and Treasureψ(`∇´)ψ
CF758E Broken Treeψ(`∇´)ψ
CF1270F Awesome Substringsψ(`∇´)ψ
CF755F PolandBall and Giftsψ(`∇´)ψ
CF1340D Nastya and Time Machineψ(`∇´)ψ
CF780G Andryusha and Nervous Barriersψ(`∇´)ψ
CF1392F Omkar and Landslideψ(`∇´)ψ
CF372D Choosing Subtree is Funψ(`∇´)ψ
CF848C Goodbye Souvenirψ(`∇´)ψ
CF1036G Sources and Sinksψ(`∇´)ψ
CF955F Heapsψ(`∇´)ψ
CF811E VAldik and Entertaining Flagsψ(`∇´)ψ
CF1680F Lenient Vertex Coverψ(`∇´)ψ
CF1699E Three Days Graceψ(`∇´)ψ
CF1208F Bits And Piecesψ(`∇´)ψ
CF1583G Omkar and Time Travelψ(`∇´)ψ
AGC032D Rotation Sortψ(`∇´)ψ
给定一个排列, 你可以花费 \(A\) 使一个区间最左边的数跑到最右边, 或者花费 \(B\) 的代价使最右边到最左边,求把整个序列变成升序的最少花费。
\(1\le n \le 5000\)。
可以注意到实际上这个东西就是你想把一个东西拿到哪里就拿到哪里。
显然对于一个元素操作次数不会超过 \(1\),而这个代价取决于它向前向后移。
所以我们要做的就是给每个元素确定,它是不动,还是往左往右移动。
往左往右这个能很自然的想到考虑没被移动的元素,具体来说我们假设前面的都已经完成,那么这个位置的状态就是,前面的,没有被移动的最后一个元素是什么。
换句话说操作到这里和它相邻的是什么,它放到哪边取决于他和没有被移动的最后一个元素的大小关系。
于是考虑一个 dp,即可解决问题。
ABC176F - Brave CHAINψ(`∇´)ψ
您有 \(3n\) 张卡片,其中每张卡片上都写着 \(1\sim n\) 中的一个数,您需要重复以下操作 \(n-1\) 次:
- 将最左侧的 \(5\) 张牌任意排列,排列后,删去最左侧的 \(3\) 张牌,如果这三张牌上写着同样的数,您可以获得 \(1\) 分。
最后,如果剩余的 \(3\) 张牌上的数字一样,那么还可以额外得到 \(1\) 分。
现在,您想要知道,得到的分数最高是多少。
\(1\ \leq\ N\ \leq\ 2000,1\ \leq\ A_i\ \leq\ N\)。
怎么一上来就王炸 /qd
最难的 ABC F,蚌埠住了,不过也不算难。
但是一个事情是我思考的时候完全没想到用 dp 来记录啊。
妈的,评价是不太会枚举套路。
考虑一个 simple 的 dp,就是考虑没被选中的两个,当前维护到 \(i\)。
\(dp(i, x, y)\) 表示当前考虑到第 \(i\) 个以及他之后的两个,之前剩下来的是 \(x,y\) 的最大得分。
暴力转移 \(O(n^3)\) 考虑优化,可以注意到能有分的转移不多,剩下的转移都只是继承。
于是我们考虑有分的转移,一种是 \(a(i, i + 1, i + 2)\) 都相等,直接删掉就行。
然后就是有两个相等,枚举一个即可,不然就考虑从 \(x, y\) 里面拿一个来转移。
第一维可以滚动数组,继承就省去了,然后空间复杂度 \(O(n^2)\),可以证明这个转移内层只会更新线性个状态,所以整体复杂度就是 \(O(n^2)\)。
AGC012C - Tautonym Puzzleψ(`∇´)ψ
定义一个串是好的当且仅当它是 \(A + A\) 的形式。
您需要构造一个长度不超过 \(200\),字符集大小不超过 \(100\) 的字符串 \(s\),使得它恰好有 \(n\) 个好子序列。
一个最 naive 的情况是考虑 \(len\) 个连续的 \(1\) 的贡献,是 \(2^{i - 1} - 1\)。
然后就是,我们考虑维护串的两部分 \(A,B\),保证 \(\Sigma_A = Sigma_B\),且 \(A,B\) 中没有重复元素。
考虑加入字符,两种形式,\(C + A + B + C\),\(A + C + B + C\),假设原来的方案已经是 \(k\),然后他们的方案数是 \(k + 1, 2k + 1\)。
可以证明在给定的条件下是能构造出来的,考虑反过来,如果是奇数就当作 \(2k + 1\) 处理,除以二,然后偶数就减一变成奇数,可以发现次数是 \(\log\) 级别,字符集大概在 \(80\) 左右不会寄。
现场思路一会补。
CF8E Beadsψ(`∇´)ψ
定义一个 01 串是好的,当且仅当它比它的 Flip,Reverse,Flip & Reverse 串字典序都小。
给定 \(n,k\),你需要求所有 \(n\) 位(比如 \(4\) 位就是 0010 0001 这种)的 01 串中,字典序第 \(k\) 小是哪个。
\(1\le n \le 50, 1\le k \le 10^{16}\)。
显然 Flip 这个操作只需要保证第一位为 \(0\) 即可。
然后我们要考虑的就只有 Reverse 和 Flip & Reverse。
考虑套路地按位确定这个数,假设当前正在确定第 \(i\) 位。
不妨假设这一位是 \(0\),然后问题在于怎么满足 \(k\) 的限制。
我们只需要算一下此时和这个前缀一致的,满足条件的串有多少,如果这个数 \(s < k\),那么显然我们需要把这一位变成 \(1\),不然方案数肯定不会增加,反之则令这一位为 \(0\),并令 \(k \gets k - s\)。
然后问题就转化成了求方案,这个可以数位 dp。
设 \(dp(i, 0/1, 0/1)\) 表示考虑确定了前 \(i\) 位和后 \(n - i + 1\) 位,前后缀的 Reverse 是否相等,Flip & Reverse 是否相等的方案数。
每次枚举第 \(i, n - i + 1\) 位的取值进行转移即可,这题的阶段性并不是很强,使用刷表法的话会比较麻烦,不妨考虑使用记忆化搜索。
另一种方式也很容易考虑到,直接二分,做法是一致的不在叙述。
ABC313Gψ(`∇´)ψ
这场 ABC 都真的重量级。
G 题是赛时出思路了我不会用类欧算贡献,哈哈。
没学过类欧是这样的。
你有一个序列 \(\{a_n\}, 1\le n\le 2e5, 0\le a_i\le 1e9\)。
你可以做以下的操作任意次。
令 \(\forall i, a_i \gets \max(0, a_i - 1)\)。
令 \(\forall i, a_i \gets a_i + 1\),如果我们把序列看成一个个石子堆,那么这个操作要求你手上至少有 \(n\) 个才能进行,第一个操作是取出一个石子。
问有多少种可能的最终序列,对 \(998244353\) 取模。
因为考场思路其实可以直接当题解用一部分,就直接放考场思路了。
\(O(n)\) 的 dp?看起来不然就是妙妙优化不然就是直接设计。
也有可能是乱搞。
思考一下,这里的操作等于是全局减一,全局ckmax(0)。和全局加一。
不妨考虑有减到 \(0\) 的就不操作,那么方案数是全局最小值。
现在会产生新方案,原因在于可以 ckmax,从而某个元素和其它元素的 gap 就减少了,然后我们再加回去就可以弄出新的方案。
但是值域 \(10^9\),有一个基于值域的暴力做法。
有个奇妙想法,如果我们对所有元素排序,再计数答案是不是也不会变,这么做是因为这里影响很杂乱,排序之后应该会好的多。
因为这里是全局啊,哦还真是,那从小到大,说不定可以找到阶段。
哦还需要考虑相等,这个也可以直接缩掉,不用关心,它们的变化一定是等同的。
然后我们的类似阶段的东西就应该是,考虑前面的石子都已经取完,对当前石子,考虑它和后面的 gap 能产生的影响有多少。
可以发现对于一个决策,当前石子数量如果知道,能直接 \(O(1)\) 算出对应的方案。
那么只需要对于一个局面确定一下它还能弄出哪些。
由操作二的使用限制,可以发现这东西分块了!整除之后一大段都是一样的不用记录,所以这个可以整除分块算啊啊啊。
但是这东西取模啊,整除分块做不了一点。
我们写出式子看看,先枚举操作一进行了多少次来枚举所有可能的 gap。
假设我们考虑第 \(i\) 堆石子,假设这里操作了 \(j\) 次。
那么操作二可以使用的次数就是 \(\lfloor\dfrac{(n - i)j + s_i}{n}\rfloor\),其中 \(s_i\) 为前缀和。
然后答案就是一大坨形如这玩意儿的求和,是一个类欧几里得算法。
AGC008Bψ(`∇´)ψ
有 \(N\) 个格子排成一列,从左起第 \(i\) 个格子中写着整数 \(a_i\)。
开始时,每个格子被涂成白色。snuke 将重复进行以下操作。
- 选择连续的 \(K\) 个格子,将它们全部涂成白色或全部涂成黑色。此操作将会覆盖掉格子原来的颜色。
snuke 希望在操作完成后,黑色格子中整数的和最大。请求出此最大值。
- \(1 \leq N \leq 10^5\)
- \(1 \leq K \leq N\)
- \(a_i\) 是整数。
- \(|a_i| \leq 10^9\)
dp 的话前面可以转移过来的状态有 \(2^K\) 个。
没想过怎么优化,不过我感觉不太能,先放着。
然后其实这个就是,有一个 observation,就是说每个位置要不然涂色要不然就不涂色,即使原来是白色,我们也不考虑这个问题。因为也可以多涂啊,或者说它就不动。
或者说有另一个想法,我们是要尽量多的用白色覆盖负数,用黑色覆盖正数。
那么对于一个 k,我们看看能不能有什么“组合技”
看起来是单个位置都能选,但是这个 \(k\) 会让这个位置的决策对后面有影响。
所以我们可能是需要钦定一个位置,前面都是一个一个取,后面都是一个一个取,然后考虑中间这段怎么合并?
发现,如果我们钦定一个方向通过重叠的方式一个一个选,后 \(k\) 个是不能一个一个选的
所以我上面说的那个东西大概率是对的。
就是钦定中间一段,前后都选正数,看中间一段选不选就行了。
AGC020Cψ(`∇´)ψ
有一个集合由 \(N\) 个整数组成,请求出它的非空子集和的中位数。
\(1\le n \le 2000, 1\le a_i \le 2000\)。
一个很显然但是很容易被忽略的结论:对于一个子集 \(p\),它关于大集合的补集 \(q\),他们的和关于 \(\left\lceil\dfrac{\sum a_i}{2}\right\rceil\) 对称,所以中位数就是比这个大的第一个子集和。
考虑可行性背包处理一下就行,然后需要 bitset 优化。
AGC008Dψ(`∇´)ψ
给你一个长度为 \(N\) 的整数序列 \(X\),请判断是否存在一个满足下列条件的整数序列 \(a\),如果存在,请构造一种方案。
条件如下:
\(a\) 的长度为 \(N^2\),并且满足数字 \(1,2, \cdots, N\) 都各出现恰好 \(N\) 次。
对于 \(1 \le i \le N\),数字 \(i\) 在 \(a\) 中第 \(i\) 次出现的位置是 \(X_i\)。
\(1\le n \le 500\)
感觉很简单啊,显然我们贪心的考虑 \(x_i\) 更靠前的,然后把 \(i - 1\) 个数填到前面,然后看看能不能填上就行了。
AGC013Cψ(`∇´)ψ
有一个长度为 \(L\) 的圆环,上面有 \(N\) 个蚂蚁,位置分别为 \(x_i\),运动方向为 \(d_i\),\(1\) 表示顺时针,\(2\) 表示逆时针。
每只蚂蚁将会同时开始以单位速度运动,如果两只蚂蚁相遇, 那么它们会改变自己的方向继续运动。
求 \(T\) 秒之后每只蚂蚁的位置。
- \(1\ \leq\ N\ \leq\ 10^5\)
- \(1\ \leq\ L\ \leq\ 10^9\)
- \(1\ \leq\ T\ \leq\ 10^9\)
- \(0\ \leq\ X_1\ <\ X_2\ <\ ...\ <\ X_N\ \leq\ L\ -\ 1\)
- \(1\ \leq\ W_i\ \leq\ 2\)
这不就是我普及组时代就做过的独木桥吗!
考虑链的情况,相对顺序是不会改变的。
碰面了可以当作直接穿过去,所以直接找到 \(1\) 在哪里就好了。
然后这里是在环上,所以考虑它经过 \(0\) 的情况特殊处理就好。
AGC018Dψ(`∇´)ψ
有一颗 \(N\) 个顶点的树,顶点依次标号 \(1\sim N\)。
第 \(i\) 条边连接着顶点\(A_i\)和\(B_i\),且第 \(i\) 条边的长度为 \(C_i\)。
有一张 \(N\) 个点的完全图,图上两点之间的边的边权为它们在树上的距离。
求最长哈密顿路径(即不重不漏恰好经过每个点一次)。
- \(2\ \leq\ N\ \leq\ 10^5\)
- \(1\ \leq\ A_i\ <\ B_i\ \leq\ N\)
- \(1\ \leq\ C_i\ \leq\ 10^8\)
我想拿出一张经典图:

这题睡着之后感觉不知道谁告诉了我一个结论,然后我就会了。
首先回路是好求的,我们去掉一个边就是路径了。
这里是完全图啊啊啊啊啊。
然后考虑一条树边,假设它断开之后左右两个块大小为 \(x, y\),那么经过他的回路最多 \(\min(x, y)\) 条,这是经典结论。
有人托梦告诉我最优方案的每一步一定经过重心,我想了想,如果只有一个重心删掉出边里权值最小的,如果两个就删去中间最小的一条边就行了。
于是我们做完了。
好吧略微严谨一点,最优解的每一步经过重心这个可以考虑,如果你不经过重心,那么会少走至少一条出子树的边,一定不优秀。
然后删边就调整法证明一下就行了。