跳转至

斜率优化

泛化ψ(｀∇´)ψ

可以斜率优化的方程通常具有以下形式：

\(dp(i) = \min\limits_{j = L(i)}^{R(i)}\{dp(j) + val(i, j)\}\)，其中 \(val(i, j)\) 为一个关于 \(i, j\) 的多项式，\(L(i), R(i)\) 为一个关于 \(i\) 的函数，用于限制 \(j\) 的范围。

并且 \(val(i, j)\) 存在形如 \(i \times j\) 的项，与单调队列优化的仅有 \(i, j\) 项不同。

斜率优化的思想是，先拆掉 \(L(i), R(i)\) 的限制，将所有决策点转化为二维平面上的点，将方程转化为一个一次函数来进行决策，在决策时再加上 \(L(i), R(i)\) 的限制，具体来说，我们建立以下映射：

  • 将仅和 \(j\) 相关的项看作 \(y\)，记这些项组成的多项式为 \(y_i\)，形如 \(dp(j) + v(j) + \dots\)。
  • 将和 \(i,j\) 同时相关的项看作 \(k,x\)，其中 \(i\) 这一部分作为 \(k\)，记为 \(k_i\)，\(j\) 这一部分作为 \(x\)，记为 \(x_j\)，式子形如 \(C_1\times(C_2 - v(i)) \times w(j)\)（其中 \(C_1,C_2\) 为常量），那么 \(k_i = C_1\times(C_2 - v(i)), x_j = w(j)\)
  • 将仅和 \(i\) 相关的项看作 \(b\)，记为 \(b_i\)，为了方便我们把常量也算进这一部分，式子形如 \(dp(i) + v(i) \times w(i) + C\)，我们要最小化的就是这一部分（本质是最小化 \(dp(i)\)，其它的是常量所以无所谓。）

（以上的式子只是做一个参考理解，需要根据实际情况来改变。）

然后，问题就转化为，给定一堆平面上的点 \((x_j, y_j)\)，对于一条直线 \(y = k_ix + b_i\)，我们需要选择一个满足 \(L(i) \le j \le R(i)\) 限制的 \((x_j, y_j)\) 代入直线，使得 \(b_i\) 最小。

可以注意到，在取 \(\min\) 时，只有下凸壳上的点可以作为最优的决策点：

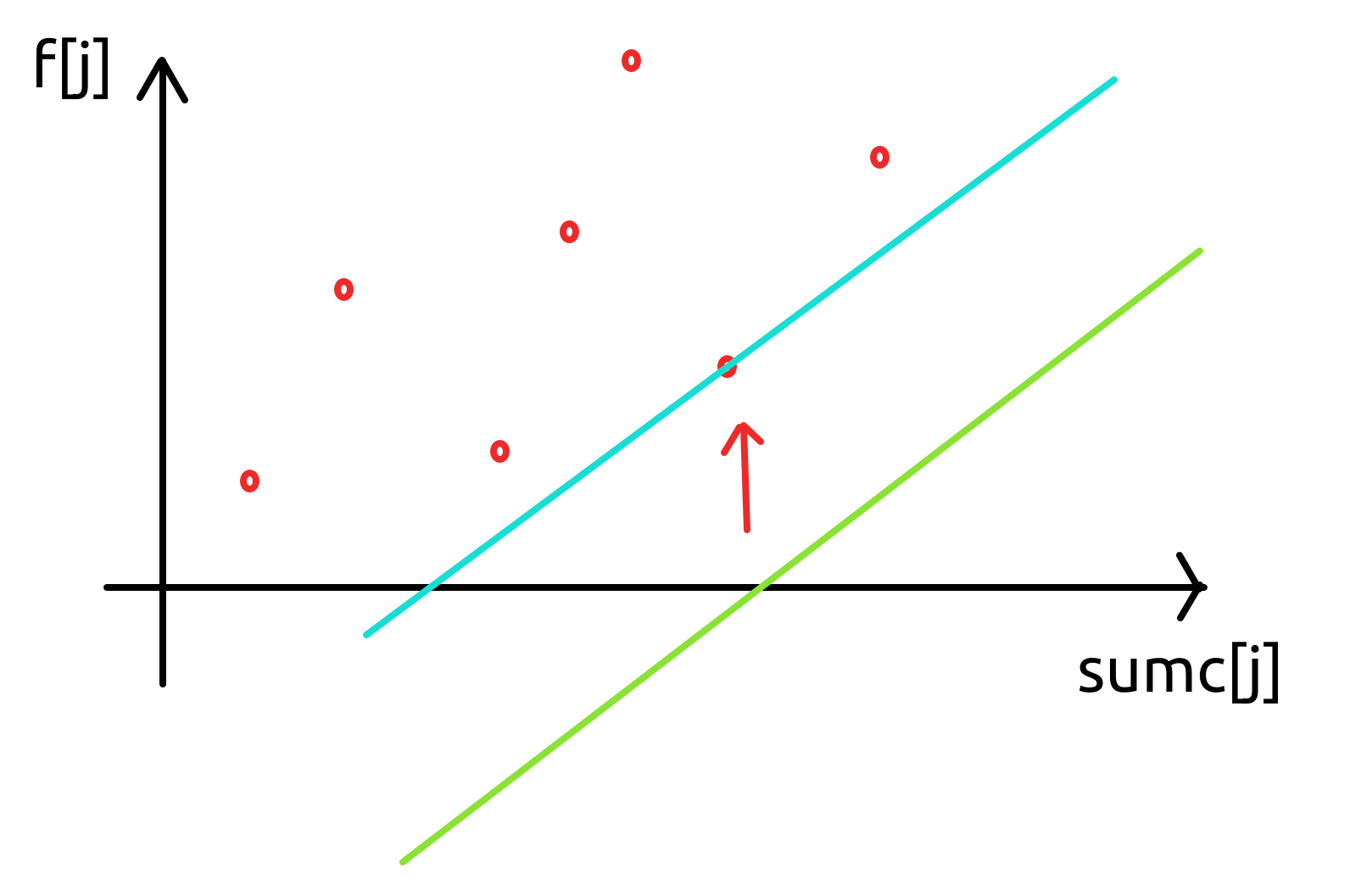
copt-2.png

（这是下面例题的例子，它的 \(y_j = dp(j), x_j = sumc(j)\)）

于是，在 \(k_i\) 随 \(k\) 单调递增，且只需要在尾部插入决策的情况下，我们只需要用单调队列来维护下凸壳上的点进行决策就行了。

具体来说，我们设 \(K(u, v)\) 表示经过 \((x_u, y_u),(x_v,y_v)\) 的直线斜率，我们保证，对于一个单调队列 \(q(l, r)\)，满足 \(\forall i\in (l,r)\)，有 \(K(i - 1, i) < K(i, i + 1)\)。

然后决策完一个点 \(i\) 之后考虑插入 \((x_i, y_i)\)，这样就能满足前缀下标限制 \(j < i\) 了（思想类似二维数点），如果是更一般的 \(L(i), R(i)\) 随 \(i\) 单调递增的约束，就在单调队列中排除冗杂即可，整个过程类似下图：

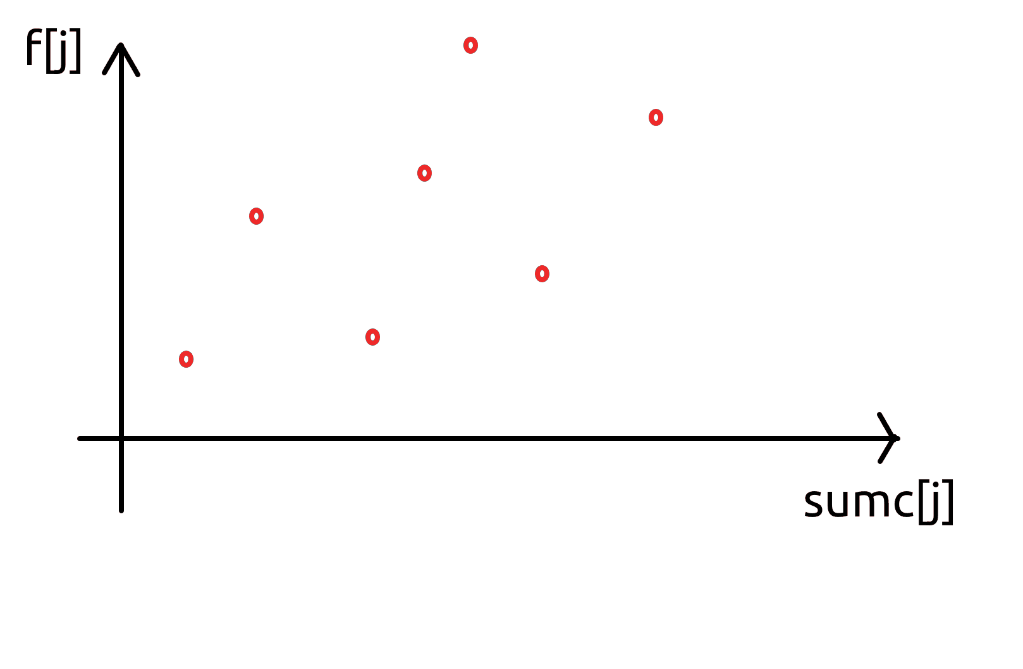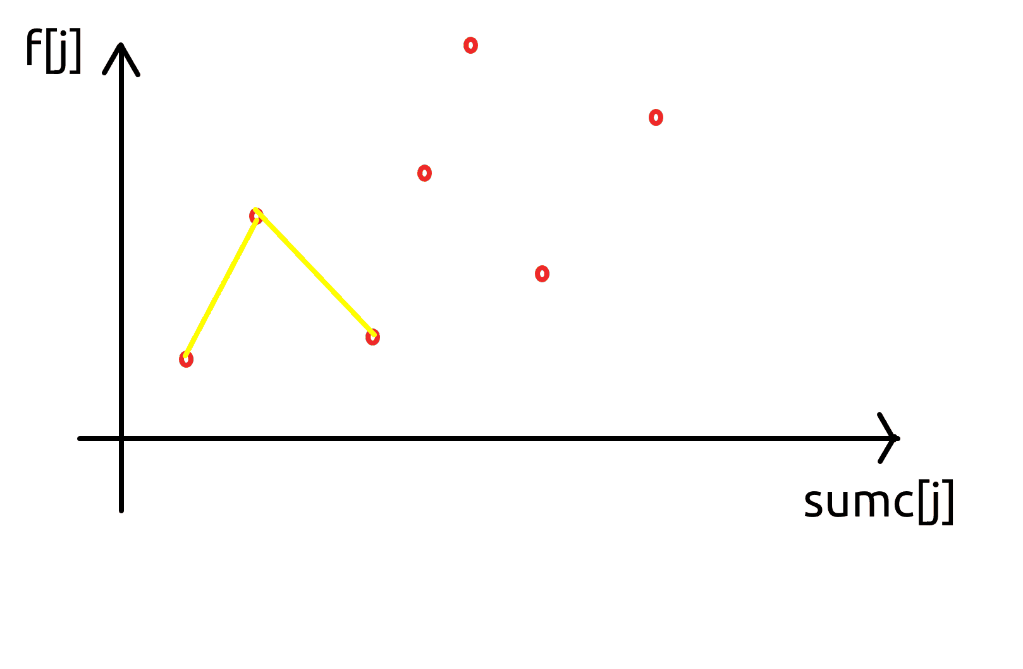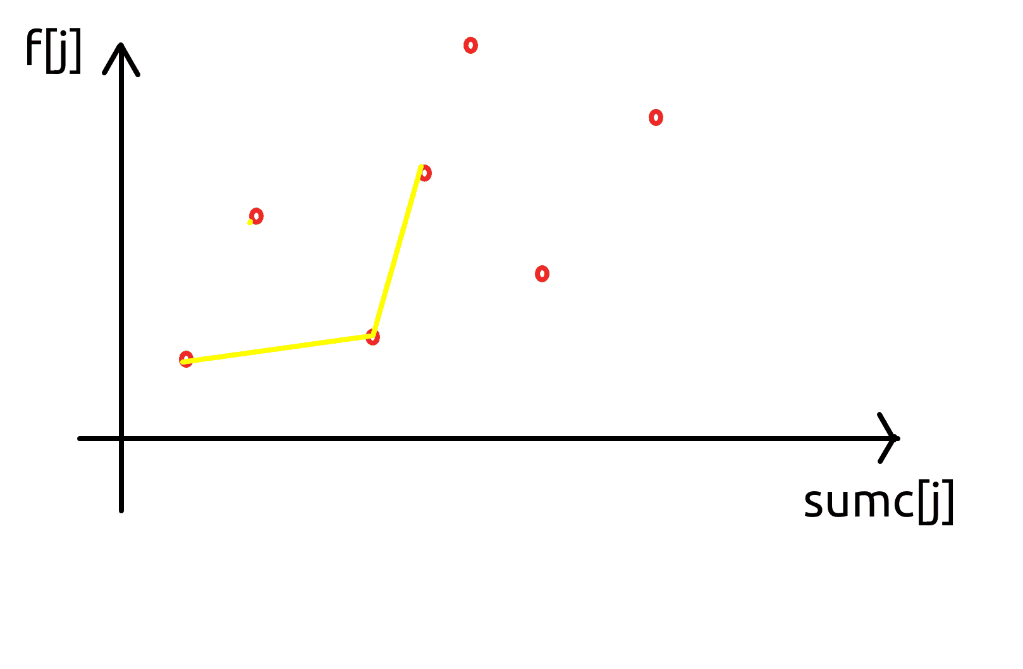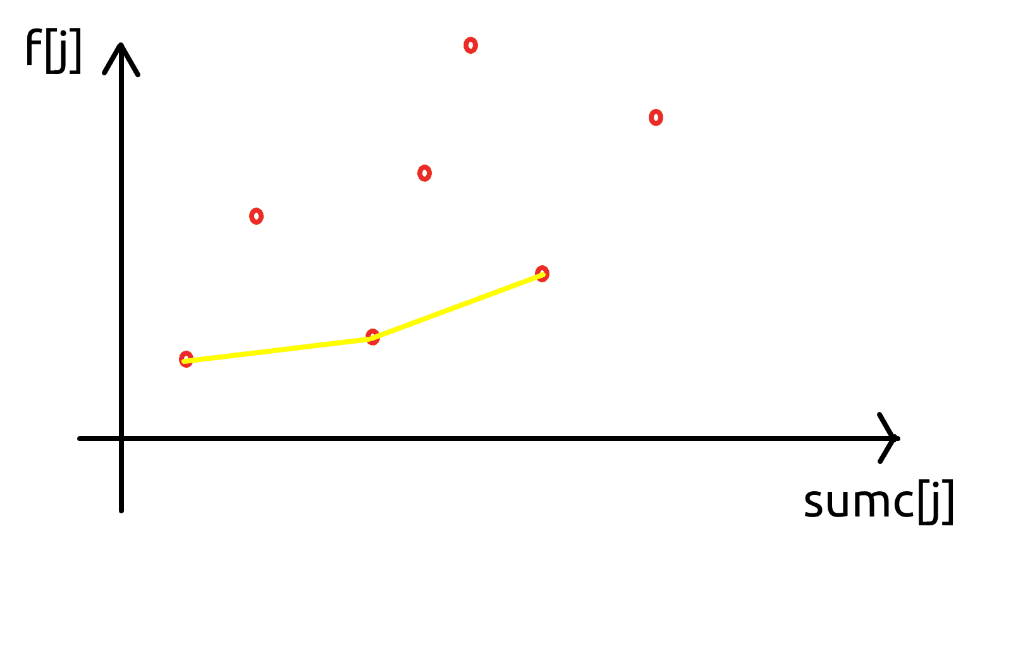
copt-5.gif

可以注意到，对于给定的 \(k_i\)，使得答案 \(b_i\) 最小的 \(j\)，一定满足 \(K(i - 1, i) < k_j < K(i, i + 1)\)，于是我们不断弹掉队头，直到找到这个点即可。

当然，如果 \(k_i\) 的变化不是单调的（没法使用单调队列），亦或是需要支持任意位置插入/删除决策，又或者是 \(L(i), R(i)\) 的变化很不好处理，我们可以考虑使用二分/平衡树/cdq分治/李超树来维护这个凸壳，这个在下面会提到。

例题ψ(｀∇´)ψ

\(n\) 个任务排成一个序列在一台机器上等待完成（顺序不得改变），这 \(n\) 个任务被分成若干批，每批包含相邻的若干任务。

从零时刻开始，这些任务被分批加工，第 \(i\) 个任务单独完成所需的时间为 \(t_i\)。在每批任务开始前，机器需要启动时间 \(s\)，而完成这批任务所需的时间是各个任务需要时间的总和（同一批任务将在同一时刻完成）。

每个任务的费用是它的完成时刻乘以一个费用系数 \(c_i\)。请确定一个分组方案，使得总费用最小。

数据范围：

I. \(n \le 500,1\le s \le 50,1\le t_i,c_i \le 100\)

II. \(n\le 5000,1\le s \le 50,1\le t_i,c_i \le 100\)

III. \(n \le 3\times 10^5,1\le s \le 512,1\le t_i,c_i \le 512\)

IV. 条件同 III，\(t_i\) 可能是负数。

V. 条件同 IV, \(c_i\) 可能是负数。

I. 暴力ψ(｀∇´)ψ

设 \(dp(i, j)\) 表示，考虑前 \(i\) 个位置，分了 \(j\) 段的最大价值。

根据定义，枚举上一个位置 \(k\)，可以得到方程：\(dp(i, j) = \min\limits_{k = 0}^{i - 1}\{dp(k, j - 1) + \sum\limits_{l = k + 1}^i c(l) \times (s \times j + \sum\limits_{l = 1}^{i} t(i))\}\)。

预处理前缀和，可以做到 \(O(n^3)\)。

Code 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
// author : black_trees

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define endl '\n'
#define int long long

using namespace std;
using i64 = long long;

const int si = 500; 
const int inf = 0x3f3f3f3f3f3f3f3fll;

int n, s;
int t[si], c[si];
int dp[si][si], st[si], sc[si];

signed main() {

    cin.tie(0) -> sync_with_stdio(false);
    cin.exceptions(cin.failbit | cin.badbit);

    memset(dp, 0x3f, sizeof dp);

    cin >> n >> s, dp[0][0] = st[0] = sc[0] = 0;
    for(int i = 1; i <= n; ++i)
        cin >> t[i] >> c[i], st[i] = st[i - 1] + t[i], sc[i] = sc[i - 1] + c[i];
    for(int i = 1; i <= n; ++i) {
        for(int j = 1; j <= i; ++j) {
            for(int k = 0; k < i; ++k) {
                dp[i][j] = min(dp[i][j], dp[k][j - 1] + (sc[i] - sc[k]) * (s * j + st[i]));
            }
        }
    }
    int ans = inf;
    for(int i = 1; i <= n; ++i) {
        ans = min(ans, dp[n][i]);
    }
    cout << ans << endl;

    return 0;
}

II. 费用提前计算ψ(｀∇´)ψ

注意到本题并不要求分多少段，用 Fence 的思路可以改进一下：

设 \(dp(i)\) 表示考虑前 \(i\) 个位置，分了若干段的代价最小值，枚举上一个位置 \(j\) 即可转移。

但是转移的时候并不能知道机器启动了多少次，所以我们用一种叫费用提前计算的思想，知道这里已经启动了一次了，就把它会对之后的所有状态做的贡献直接加到当前状态里面，也就是，对于后面的所有任务，可以知道这些任务又多出了 \(s\) 的时间，那么决策到后面的任务时，影响就被消除了。

可以得到：\(dp(i) = \min\limits_{j = 0}^{i - 1} \{dp(j) + \sum\limits_{k = j + 1}^{n} c(k) \times s + \sum\limits_{k = j + 1}^{i} c(k) \times \sum\limits_{k = 1}^{i} t(i)\}\)

换句话说，我们是把上面那个方程的 \(s \times j \times \sum\limits_{l = k + 1}^{i} c(l)\) 移动到前面的状态进行计算了。

复杂度 \(O(n^2)\)。

Code 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
// author : black_trees

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define endl '\n'
#define int long long

using namespace std;
using i64 = long long;

const int si = 5e3 + 10;
const int inf = 0x3f3f3f3f3f3f3f3fll;

int n, s;
int t[si], c[si];
int st[si], sc[si];
int dp[si];

signed main() {

    cin.tie(0) -> sync_with_stdio(false);
    cin.exceptions(cin.failbit | cin.badbit);

    memset(dp, 0x3f, sizeof dp);

    dp[0] = st[0] = sc[0] = 0, cin >> n >> s;
    for(int i = 1; i <= n; ++i)
        cin >> t[i] >> c[i], st[i] = st[i - 1] + t[i], sc[i] = sc[i - 1] + c[i];
    for(int i = 1; i <= n; ++i) {
        for(int j = 0; j < i; ++j) {
            dp[i] = min(dp[i], dp[j] + (sc[n] - sc[j]) * s + (sc[i] - sc[j]) * st[i]);
        }
    }
    cout << dp[n] << endl;

    return 0;
}

III. 斜率优化ψ(｀∇´)ψ

考虑用前缀和写下 II 的式子：

\(dp(i) = \min\limits_{j = 0}^{i - 1}\{dp(j) + (sc(n) - sc(j)) \times s + (sc(i) - sc(j)) \times st(i)\}\)

乘开：\(dp(i) = \min\limits_{j = 0}^{i - 1}\{dp(j) + sc(n) \times s - sc(j) \times s + sc(i) \times st(i) - sc(j) \times st(i)\}\)

套用斜率优化的板子，我们去掉 \(\min\)：

\(dp(i) = dp(j) + sc(n) \times s - sc(j) \times s + sc(i) \times st(i) - sc(j) \times st(i)\)

写成一次函数 \(b = -kx + y\)的形式：

\(dp(i) - sc(i) \times st(i) - sc(n) \times s = -(st(i) + s) \times sc(j) + dp(j)\)

所以 \((x, y)\) 这些点就是 \((sc(j), dp(j))\) 的形式，我们现在需要让 \(dp(i)\) 尽可能的小，就是让以 \((st(i) + s)\) 为斜率的直线经过一个最优的 \((sc(j), dp(j))\)。

因为下标限制是 \(j \in [0, i)\)，\(k_i\) 随 \(i\) 单调递增，且只需要在末尾插入决策，所以一个一个决策完插入单调队列就好了。

Code 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
// author : black_trees

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define endl '\n'
#define int long long

using namespace std;
using i64 = long long;

const int si = 5e3 + 10;
const int inf = 0x3f3f3f3f3f3f3f3fll;

int n, s;
int t[si], c[si];
int st[si], sc[si], dp[si];
int q[si], l, r;


signed main() {

    cin.tie(0) -> sync_with_stdio(false);
    cin.exceptions(cin.failbit | cin.badbit);

    st[0] = sc[0] = 0;
    memset(q, 0, sizeof q), l = 1, r = 1;
    memset(dp, 0x3f, sizeof dp), dp[0] = 0;
    // 让 (x0, y0) 入队（j 可以取到 0）
    // 队列本身还是闭区间，但是为了保证 l + 1, r - 1 不会越界，所以写的是 l < r.

    cin >> n >> s;
    for(int i = 1; i <= n; ++i)
        cin >> t[i] >> c[i], sc[i] = sc[i - 1] + c[i], st[i] = st[i - 1] + t[i];
    for(int i = 1; i <= n; ++i) {
        while(l < r &&  
            dp[q[l + 1]] - dp[q[l]] <= (st[i] + s) * (sc[q[l + 1]] - sc[q[l]]))
                ++l;
        dp[i] = dp[q[l]] - (st[i] + s) * sc[q[l]] + sc[i] * st[i] + sc[n] * s; 
        while(l < r && 
            (dp[q[r]] - dp[q[r - 1]]) * (sc[i] - sc[q[r]]) >= (dp[i] - dp[q[r]]) * (sc[q[r]] - sc[q[r - 1]]))
                --r;
        q[++r] = i;
    }
    // 为了避免精度问题，直接把斜率的式子写出来，分母乘到对面。

    cout << dp[n] << endl;

    return 0;
}

IV. 二分ψ(｀∇´)ψ

注意到 \(t_i\) 可能是负数，意味着 \(\exists i, st(i) < 0\)。

下标限制依然可以一个一个插入来满足，但是因为 \(k_i\) 不是单调的，所以我们没法直接扔到单调队列里面均摊 \(O(1)\) 转移（不然你更新完 \(i - 1\) 的时候可能把 \(i\) 的最优选择给弹掉）。

注意到 \(sc(i)\) 仍旧是单调的，换句话说我们只需要支持在末尾插入决策点.

那么我们仍旧可以使用单调队列维护这个凸壳，但是现在，我们需要在凸壳上直接二分一个位置 \(e\)，使得 \(K(e - 1, e) < k_i < K(e, e + 1)\) 而不是直接取队头更新，注意需要特殊判断头尾。

注意这里应该是判 \(q(mid), q(mid + 1)\) 构成的直线斜率，不然以这样的二分方式会出错（原因很简单，可以手模一下）。

Code 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
// author : black_trees

#include <cmath>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <iostream>
#include <algorithm>

#define endl '\n'

using namespace std;
using i64 = long long;
using i128 = __int128_t;

template <typename __Tp> void read(__Tp &x) {
    int f = x = 0; char ch = getchar();
    for (; !isdigit(ch); ch = getchar()) if (ch == '-') f = 1;
    for (; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + (ch ^ 48);
    if (f) x = -x;
}
void read(char &ch) { for (ch = getchar(); isspace(ch); ch = getchar()); }
template <typename __Tp1, typename ...__Tp2> void read(__Tp1 &x, __Tp2 &... y) { read(x), read(y...); }
template <typename __Tp> void write(__Tp x) {
    if (x < 0) putchar('-'), x = -x;
    if (x > 9) write(x / 10);
    putchar(x % 10 + 48);
}
void write(char ch) { putchar(ch); }
void write(const char *s) { for (; *s; ++s) putchar(*s); }
template <typename __Tp1, typename ...__Tp2> void write(__Tp1 x, __Tp2 ... y) { write(x), write(y...); }

const int si = 3e5 + 10;

int n, q[si], s, l, r;
i128 dp[si], st[si], sc[si];

int find(int slope) {
    if(l == r) return q[l];
    int L = l, R = r;
    while(L < R) {
        int mid = (L + R) >> 1;
        if(dp[q[mid + 1]] - dp[q[mid]] <= slope * (sc[q[mid + 1]] - sc[q[mid]]))
            L = mid + 1;
        else R = mid;
    }
    return q[L];
}

int main() {

    // cin.tie(0) -> sync_with_stdio(false);
    // cin.exceptions(cin.failbit | cin.badbit);

    memset(q, 0, sizeof q);
    memset(dp, 0x3f, sizeof dp);
    dp[0] = 0, l = 1, r = 1;

    read(n, s);
    for(int i = 1; i <= n; ++i) {
        i128 t, c; read(t, c);
        st[i] = st[i - 1] + t, sc[i] = sc[i - 1] + c;
    }
    for(int i = 1; i <= n; ++i) {
        int p = find(s + st[i]);
        dp[i] = dp[p] - (s + st[i]) * sc[p] + st[i] * sc[i] + s * sc[n];
        while(l < r && 
            (dp[q[r]] - dp[q[r - 1]]) * (sc[i] - sc[q[r]]) >= (dp[i] - dp[q[r]]) * (sc[q[r]] - sc[q[r - 1]]))
            --r;
        q[++r] = i;
    }

    write(dp[n], endl);

    return 0;
}

V. 平衡树/CDQ 分治/李超树ψ(｀∇´)ψ

注意到 \(\exists i, sc(i) < 0\)，也就是说 \(sc(i)\) 也不是单调递增的了，我们可能在任意的位置插入决策点。

下标限制还是可以一个一个插入来满足，那么有一个不动脑子的做法，直接用平衡树维护凸壳，二分转化为在平衡树上二分。

还有一种聪明一点的做法是使用 CDQ 分治。

就是说，CDQ 分治的一个重要应用就是，把一个动态问题转化为静态问题，我们可以利用这个思想，将需要动态插入的凸壳转化为静态的凸壳。

具体来说，设 \(\text{Solve}(l, r)\) 表示计算 \([l, r]\) 的 \(dp(i)\)，分三步：

  1. 递归计算 \(\text{Solve}(l, mid)\)。
  2. 此时 \(dp(l \sim mid)\) 已经计算出来，我们考虑维护 \([l, mid]\) 这一段的所有决策点构成的凸壳，这个可以使用单调队列，但是要先按照 \(x\) 排序（因为本来就是乱序嘛，你现在只更新 \([mid + 1, r]\) 的，前面的下标顺序没啥影响，排序也没事，只要最后复原一下就好了），然后我们对于 \(dp(mid + 1\sim r)\)，考虑从这个凸壳上更新答案，这部分可以二分（因为斜率不是单调的嘛）。
  3. 递归计算 \(\text{Solve}(mid + 1, r)\)，我们这里使用的是“中序遍历”，所以 dp 转移的正确性是有保证的，而 \(dp(mid + 1, r)\) 显然不可能只在 \([l, mid]\) 上取到最优，这个递归计算的过程就可以直接算出 \(dp(mid + 1, r)\)。

如果有删除操作，或者说对于一个 \(i\)，它的 \(L(i), R(i)\) 变化很不均匀，我们仍旧可以使用 CDQ 分治，每次在凸壳上二分的时候就直接取满足 \([u, v] \in [L(i), R(i)]\) 的一段来二分就行了。

如果出题人比较**，给你来一个中间扣掉一个的删除，就比较恶俗，不过好像可以转化成 CDQ 里面的 修改-询问关系？是不是还可以线段树分治 + 李超树？不过这样子的话，平衡树维护就是最简单的了，这里用 Leafy Tree 可能会比较简单。

李超树的话，因为不支持删除所以有一定的局限性，所以大部分时候我们还是使用 CDQ 分治，不过这题因为 \(L(i), R(i)\) 的限制比较 trivial 所以李超树也是可以做的。

Tips：记得判斜率不存在的情况哦。

Code(CDQ,不带删除操作)

代码暂略，已经查出错了，找个时间来写。

总结ψ(｀∇´)ψ

斜率优化的思想在泛化里已经说了，在这里提一提对于决策点集合的维护方式：

  • 对于 \(L(i), R(i)\) 的下标限制：
    • 如果是类似本题的 \(0 \le j < i\)，说明不需要删除决策点，而且每次只会在尾部插入决策，我们枚举就好了
    • 如果 \(L(i), R(i)\) 是随 \(i\) 单调变化的，我们就需要使用单调队列来排除冗杂
    • 如果是没啥单调性的，也就是说一般要支持在任意位置插入删除决策点，就需要使用平衡树或者 CDQ 分治。
  • 对于斜率的限制，只需要看斜率是否单调递增即可：
    • 如果斜率随 \(i\) 单调递增，那么可以直接使用单调队列取队头转移。
    • 如果斜率不随 \(i\) 单调递增，我们就需要在凸壳上二分答案找到最优决策点。
  • 对于 \(x_j\) 的限制，只需要看它是否随 \(j\) 单调递增即可。
    • 如果它随 \(j\) 单调递增，那么我们就只需要一个一个插入决策就行。
    • 如果它不随 \(j\) 单调递增，那么我们就需要使用平衡树 / CDQ 分治来支持插入决策点的操作，注意 CDQ 维护的时候还要对前一半排序。

Last but not least: 如果使用交叉相乘来避免精度问题，要小心数据范围，如果直接使用浮点数，要记得，eps 不要开太小了，要视情况而定。

习题ψ(｀∇´)ψ

见 CWOI 斜率优化专题

最后更新: October 13, 2023