二分图

定义

如果一张无向图 \(G\) 可以分成两个不相交的点集 \(A,B\) ，且点集当中的点相互之间没有连边，则称 \(G\) 为一张二分图。

\(A,B\) 分别称为 \(G\) 的左部和右部。

判定

定理：无向图 \(G\) 是二分图，当且仅当图中不存在奇环。

所以可以用染色法判定无向图 \(G\) 是不是二分图。

进行黑白的间隔染色，如果出现冲突，那么图中必然存在奇环，\(G\) 不是二分图。

int color[si_n];
bool ok=true;
inline void dfs(int u,int col){
    color[u]=col;
    for(register int i=head[u];~i;i=e[i].Next){
        int v=e[i].ver;
        if(!color[v]) dfs(v,3-col);
        else if(color[v]==col) ok=false;
    }
}
// in main()
memset(color,0,sizeof color);
for(register int i=1;i<=n;++i) if(!color[i]) dfs(i,1);

复杂度 \(\text{O}(n+m)\)。

最大匹配

匹配：任意两条边都没有公共端点的边集称为图的一组匹配 \(S\)。

二分图最大匹配：二分图当中，边数最多的一组匹配为二分图的最大匹配。

在 \(S\) 当中的边被称为匹配边，其它的边称为非匹配边，匹配边的端点是匹配点，其它节点被称为非匹配点。

如果二分图上存在一条路径 \(\delta(u,v)\) ，连接 \(u,v\) 这两个非匹配点，使得 \(S\) 的匹配边和非匹配边在路径上交替出现，称 \(\delta(u,v)\) 为匹配 \(S\) 的增广路。

如图，\(\delta(u,v)\) 即为一条增广路：

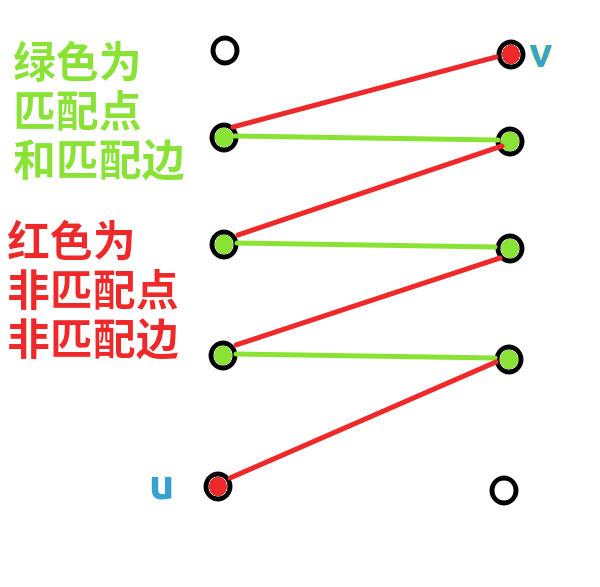
需要注意的是，先定义的是匹配点和匹配边，剩下的才是非匹配边和匹配点。

所以连接两个匹配点的不一定是匹配边，但端点带有非匹配点的边一定是非匹配边。

可以发现，增广路具有以下性质：

1. 边数为奇数
2. 第 \(1,3,5,...\) 条边是非匹配边，第 \(2,4,6,...\) 条边是匹配边。

所以，可以对增广路上的边的状态取反，得到的匹配数必然会增加 \(1\)。

从而可以得到定理：

二分图的一组匹配 \(S\) 是最大匹配，当且仅当图中不存在 \(S\) 的增广路。

对应的有一个匈牙利算法，可以利用增广路求出二分图 \(G\) 的最大匹配。

思路是：

1. 最开始先令 \(S=\emptyset\) ，然后寻找一个增广路，取反，得到新匹配 \(S\prime\)。
2. 重复直到不存在增广路。

寻找增广路的时候分两种情况给一个左部节点 \(x\) 寻找一个匹配的右部节点 \(y\)：

1. \(y\) 就是非匹配点，\((x,y)\) 本身就是增广路。

2. \(y\) 已经和另外一个左部节点匹配，但是这个左部节点 \(u\) 还能找到另外的右部节点 \(v\) 匹配。

则 \(x\to y \to u \to v\) 是一条增广路 .

bool vis[si_n];
int match[si_n];
inline bool dfs(int u){
    for(register int i=head[u];~i;i=e[i].Next){
        int v=e[i].ver;
        if(!vis[v]){
            vis[v]=true;
            if(!match[v] || dfs(match[v])){
                match[v]=u; return true;
            } // 寻找增广路的两种情况
        }
    } return false;
}

// in main()
int res=0;
for(register int i=1;i<=n;++i){
    memset(vis,false,sizeof vis);
    if(dfs(i)) res++;
} // 只用从左部开始
// 连边的时候似乎可以只连从左部到右部的有向边

复杂度 \(\text{O}(nm)\) ，但一般卡不满。

建图连边的时候似乎可以只连从左部到右部的有向边？

如果连无向边似乎也一样。

[CH6801] 棋盘覆盖

给定一个 \(n\times m\) 的棋盘，有些地方不能放，求最多能放多少个 \(1\times 2\) 或者 \(2\times 1\) 的骨牌。

且骨牌不能重叠。

\(n,m\le 100\)。

二分图最大匹配的模型需要找到两个要素：

• \(0\) 要素：节点能分成两个独立的集合，且集合内部没有边
• \(1\) 要素：每个节点只能和一条匹配边相连。

骨牌不能重复，对应的就是 \(1\) 要素，所以可以把骨牌看作边，骨牌可以占用的两个格子分别当作左部和右部节点。

所以对棋盘黑白染色，那不管怎么样，骨牌必然连接的是左右部各一个节点。

把 ban 掉的格子除外就可以了。

（用横纵坐标的和的奇偶性取分左右部节点即可）

连边的时候只需要从左部连到右部就行。

求出的最大匹配就是答案。

[CH6802] 車的放置

给定一个 \(n \times m\) 的棋盘，有一些格子不能放。

问最多可以放多少个互不攻击的車，\(n,m \le 200\)。

发现一个車的攻击范围是一行和一列。

所以可以发现一个 \(1\) 要素：每行每列最多一个車。

然后可以考虑把行和列看作点，棋子看作边，因为一个棋子不可能同时出现在两行或者两列，所以这就是 \(0\) 要素。

那么整张图就是二分图，跑最大匹配即可。

最小点覆盖

给定一张二分图 \(G\)，求出一个最小的点集 \(S\) ，使得图中任意的一条边都至少有一个端点属于 \(S\)。

则称 \(S\) 为二分图 \(G\) 的最小点覆盖。

有 \(K\ddot{o}nig\) 定理：二分图 \(G\) 的最小点覆盖包含的点数等于 \(G\) 的最大匹配包含的边数。

证明略，但是提一个构造方式：

先求最大匹配 \(S\)。

从左部的每一个非匹配点出发，再做一次 dfs 找增广路并标记访问过的节点。

最后左部没有被标记的点，右部被标记的点就是最小点覆盖。

[POJ1325] Machine Schedule

给两台初始为模式 \(0\) 的机器 \(A,B\)，分别有 \(0\sim N-1,0 \sim M-1\) 这几种模式。

给定 \(K\) 个 \(a[i],b[i]\) 表示第 \(i\) 个任务在 \(A/B\) 上运行所需要的模式。

任务执行顺序任意，但是机器只要转换模式就要重启。

求最少重启次数。

\(N,M,K \le 100\)。

二分图最小点覆盖的要素只有一个

• \(2\) 要素：每条边有两个端点，二者至少选一个。

本题的选择哪一个机器就是端点，任务就是边。

所以把任务作为边，\(A\) 的模式 \(0 \sim N-1\) 作为左部，\(B\) 的模式 \(0 \sim M-1\) 作为右部节点。

然后求最小点覆盖即可。

因为初始是 \(0\) ，所以 \(a[i],b[i]\) 只要有一个是 \(0\) 就可以不用管这个任务了。

[POJ2226] Muddy Fields

给一个 \(n\times m\) 的格子图，有些地方是脏的。

用若干个可以重复覆盖的，可以 90 度旋转的，宽为 \(1\) ，长度任意的板子覆盖所有脏的格子。

且不能覆盖干净的格子，求最小需要多少个板子。

\(n,m \le 50\)。

这题如果直接从格子作为点来匹配是找不到什么思路的。

发现题目中说可以旋转 90 度，那么对于每个格子，覆盖它的不是上下方向的就是左右方向的板子。

并且题目中说可以重复覆盖，只要被覆盖过都行。

这句话暗示了一个类似于位运算的 “或” 的条件，可以把他转化成 “至少”。

所以可以考虑把行和列看作节点，格子作为边，类似上面的 “車的放置”。

但是发现直接这样做的话，如果出现这样的情况就会出事 ： .*.*.*.。

上述做法会直接在这一行放一个，而忽略了不能覆盖干净的格子的条件。

所以可以考虑对于每个脏格子的连通块单独跑最小点覆盖。

但是复杂度会爆炸，所以考虑能达到同样效果的另一个做法：

对于每个脏连通块，把它分成宽度为 \(1\) 的 “行脏连通块”和“列脏连通块”，可以看作直接放了块同等大小的板子上去。

然后对于每个点，连接它所在的“行脏连通块”和“列脏连通块”，跑最小点覆盖即可。

最大独立集

给一张二分图 \(G\)，求出一个点集 \(S\) 使得 \(S\) 当中的点都没有边相连。

最大的 \(S\) 则称为 \(G\) 的最大独立集。

最大团定义相反，是任意两点之间都有连边的一个子图。

定理：无向图 \(G\) 的最大团等于其补图的最大独立集。

一般无向图的最大团和最大独立集是 NPC。

定理：对于一个二分图 \(G\)，\(G\) 的最大独立集的大小等于节点个数减去最小点覆盖数。

利用定义即可证明。

[CH6901] 骑士放置

给一个 \(n\times m\) 的棋盘。有一些点不能放，问最多可以放多少个国际象棋的骑士。

骑士在格子上按照日字攻击，和中国象棋的马有一定区别（没有别马腿）。

可以发现相互不能攻击就是求最大独立集。

所以可以把每一个可以防止的节点当作一个节点和它能到达的节点连边。

黑白染色之后可以发现构造的图必然是二分图。

所以找到所有左部节点，连边，求最大独立集即可。

最小路径点覆盖

给定一张 DAG，要求用尽量少的 不相交 路径覆盖整张图的所有顶点。

这就是最小路径点覆盖。

拆点二分图：对于一张 DAG，设它有 \(N\) 个节点，把原图的每个节点拆成两个节点，左部的编号为原编号，右部的编号为原编号 \(+N\)。

对于原图的一条有向边 \((x,y)\)，连接新图上的 \((x,y+n)\)。

得到的二分图称为这个 DAG 的拆点二分图，一般记作 \(G_2\)。

定理：一张 DAG 的最小路径点覆盖包含的路径条数等于它的点数减去它的拆点二分图的最大匹配数。

证明用定义+ 一些讨论即可。

最小路径可重复点覆盖

路径可以相交。

那么先对这个 DAG 做传递闭包得到一张新的 DAG，这个新 DAG 的最小路径点覆盖就是原 DAG 的最小路径可重复点覆盖。

[Bzoj2718/1143] Vani 和 Cl2 捉迷藏

Vani 和 cl2 在一片树林里捉迷藏。

这片树林里有 \(N\) 座房子，\(M\) 条有向道路，组成了一张有向无环图。

树林里的树非常茂密，足以遮挡视线，但是沿着道路望去，却是视野开阔。

如果从房子 \(A\) 沿着路走下去能够到达 \(B\)，那么在 \(A\) 和 \(B\) 里的人是能够相互望见的。

现在 cl2 要在这 \(N\) 座房子里选择 \(K\) 座作为藏身点，同时 Vani 也专挑 cl2 作为藏身点的房进去寻找，为了避免被 Vani 看见，cl2 要求这 \(K\) 个藏身点的任意两个之间都没有路径相连。

为了让 Vani 更难找到自己，cl2 想知道最多能选出多少个藏身点。

明显就是要求最小路径可重复点覆盖。

所以先做一个传递闭包，然后拆点，求最小路径点覆盖即可。

---

最后更新: May 9, 2023