最近公共祖先

概述

大概就是给你树上的两个节点，然后问他们共同的祖先里深度最大的那一个。

倍增 LCA

考虑设 \(f_{i,j}\) 表示 \(i\) 的 \(2^j\) 级祖先。

这个可以倍增递推 。 \(f_{i,j}=f_{f_{i,j-1},j-1}\)。

然后现在给定一个询问 \(lca(u,v)\)，考虑把深度较大的那一个往上跳到它的 \(2\) 的 \(\log_2n,\log_2n-1,\dots 0\) 级祖先（此处是从大到小枚举）

其本质就是倍增地往上跳。

（每个都试一试，如果这个祖先 \(f_{u,i}\) 的深度 \(dep_{f_{u,i}}\) 大于等于原来深度更小的点的深度 \(dep_v\)，就跳到这个祖先 \(f_{u,i}\)）。

如果此时两个节点重合了，LCA 就是原来深度小的节点。

否则保持两个节点的深度一致，然后各自往上跳 \(2\) 的 \(\log_2n,\log_2n-1,\dots 0\) 次幂步，并且保持上跳之后仍然不相遇。

这个过程结束之后， \(u,v\) 当前的父亲必然相同，这就是要求的 LCA。

Code

int dep[si_n],f[si_n][20];
inline void dfs(int u,int fa){
    dep[u]=dep[fa]+1,f[u][0]=fa;
    for(register int i=1;i<=19;++i) 
        f[u][i]=f[f[u][i-1]][i-1];
    for(register int i=e[u].head;i;i=e[i].Next){
        int v=e[i].ver; 
        if(v==fa) continue;
        dfs(v,u);
    }
}
inline void lca(int x,int y){
    if(dep[x]<dep[y]) swap(x,y);
    for(register int i=19;i>=0;--i) 
        if(dep[f[x][i]]>=dep[y]) 
            x=f[x][i];
    if(x==y) return x;
    for(register int i=19;i>=0;--i) 
        if(f[x][i]!=f[y][i]) 
            x=f[x][i],y=f[y][i];
    return f[x][0];
}

单次询问 \(\text{O}(\log n)\)。

但是这种方式是暴力跳，也就是直接“试”。

用类似快速幂的思想，直接把数字二进制拆分，只有当前位 \(i\) 为 \(1\) 的时候 ，才跳 \(2^i\) 级祖先。

// 咕咕咕

Tarjan LCA

首先离线所有的 Query，

在深度优先遍历的时候，给每个节点打上一个标记

1. 没有访问的节点
2. 当前正在访问的分支上的节点
3. 已经访问完并且回溯完的节点

如图：

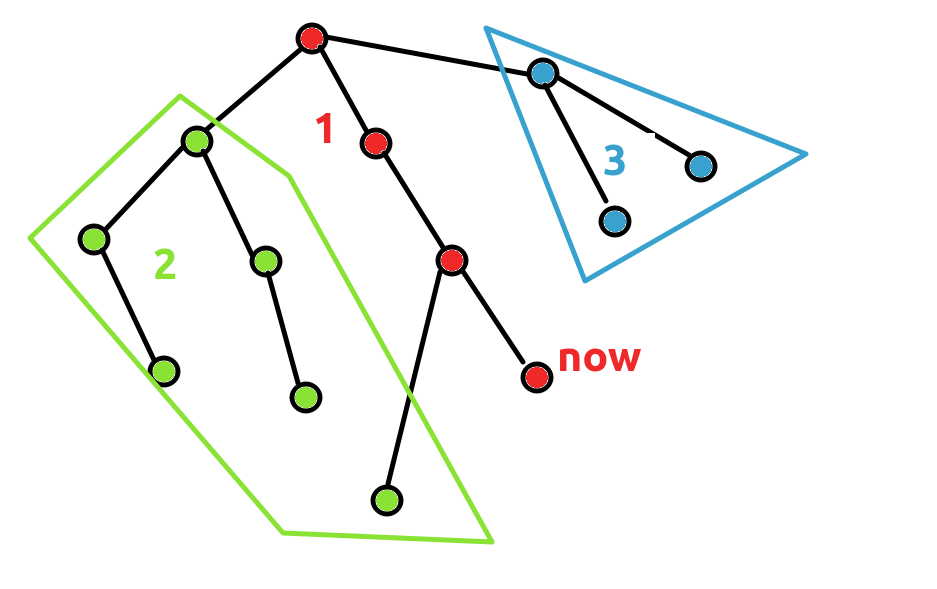
我们考虑处理所有和 \(now\) 相关的询问。

发现所有 2 类型的节点和 \(now\) 的 LCA 都是 1 类型的节点并且和 \(now\) 在同一分支，比 \(now\) 先访问：

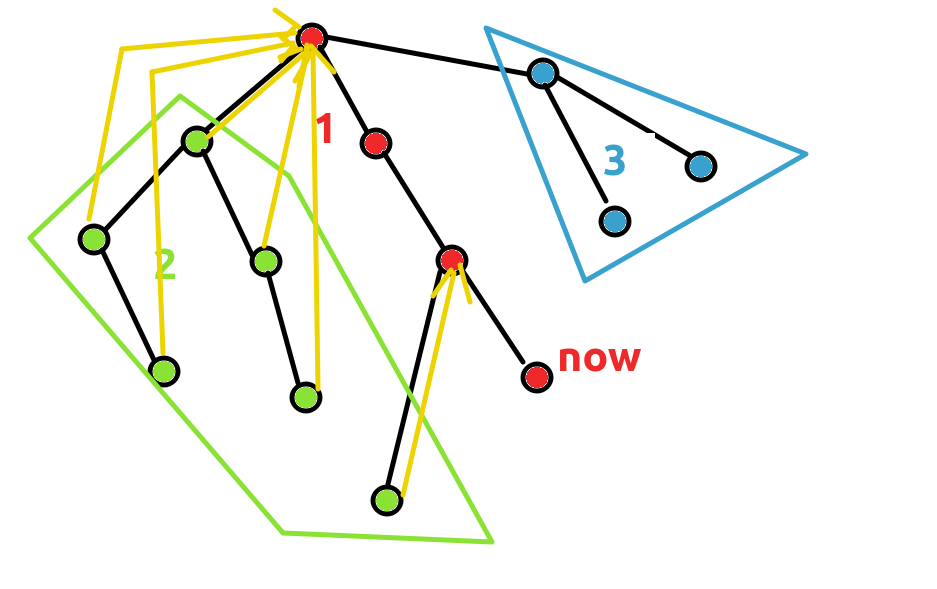
所以可以考虑把这些 2 类型的节点和当前分支的节点合并，然后每次询问就能直接处理了。

这个合并和询问操作可以利用 dsu。

复杂度 \(\text{O}(n+m)\)。

Code

#include<bits/stdc++.h>
using namespace std;

#define pb push_back
const int si_n=5e5+10;
const int si_m=5e5+10;

struct Tree{
    int ver,Next,head;
}e[si_m<<1];
int cnt=0;
void add(int u,int v){
    e[++cnt].ver=v,e[cnt].Next=e[u].head;
    e[u].head=cnt;
}

int pa[si_n];
int root(int x){
    if(pa[x]!=x){
        return pa[x]=root(pa[x]);
    }
    return pa[x];
}
vector<int>que[si_n],pos[si_n];
int lca[si_n];
bool vis[si_n];
int n,q,s;

void tarjan(int u){
    vis[u]=true;
    for(register int i=e[u].head;i;i=e[i].Next){
        int v=e[i].ver;
        if(vis[v]==true) continue;
        tarjan(v),pa[v]=root(u);
    }
    for(register int i=0;i<(int)que[u].size();++i){
        int v=que[u][i],po=pos[u][i];
        if(vis[v]==true) lca[po]=root(v);
    }
}

int main(){
    scanf("%d%d%d",&n,&q,&s);
    for(register int i=1;i<=n;++i){
        pa[i]=i,vis[i]=false;
        que[i].clear(),pos[i].clear();
    }
    for(register int i=1;i<n;++i){
        int u,v;
        scanf("%d%d",&u,&v);
        add(u,v),add(v,u);
    }
    for(register int i=1;i<=q;++i){
        int u,v;
        scanf("%d%d",&u,&v);
        if(u==v) lca[i]=u;
        else{
            que[u].pb(v),que[v].pb(u);
            pos[u].pb(i),pos[v].pb(i);
        }
    }
    tarjan(s);
    for(register int i=1;i<=q;++i){
        printf("%d\n",lca[i]);
    }
    return 0;
}

树剖 LCA

常数非常小的 LCA 求法，只不过要写两个 dfs....

简单来说还是利用了类似倍增的思想，不过利用了轻重链剖分的性质去优化了一下而已。

Link

树上差分

点差分

给你一棵树 \(T\)，且 \(\forall u \in T\) 都有一个权值 \(val[u]\)

现在有 \(q\) 次操作，每一次操作 \(\operatorname{change}(u,v,d)\) 需要你修改 \(u \to v\) 的路径上的所有点的权值，即令 \(\forall val[u]+d,(u\in \delta(u,v))\) 。

将一条树链拆成 \(A:(u,lca(u,v)),B:(v,lca(u,v))\) 这两部分。

设 \(c[u]\) 表示 \([u]\) 这个节点的增量（差分数组）。

对于 \(A,B\) 的端点分别差分一下： \(c[u]=d,c[v]=d,c[lca]=-2\times d\)。

但是这个 \(\texttt{LCA}\) 本身就在树链 \(\delta(u,v)\) 上。

所以它自己也要加 \(d\)，那么 \(c[u]=d,c[v]=d,c[lca]=-d\)。

因为父节点的值是会被子树影响的，所以还需要给 \(father(lca(u,v))-d\)。

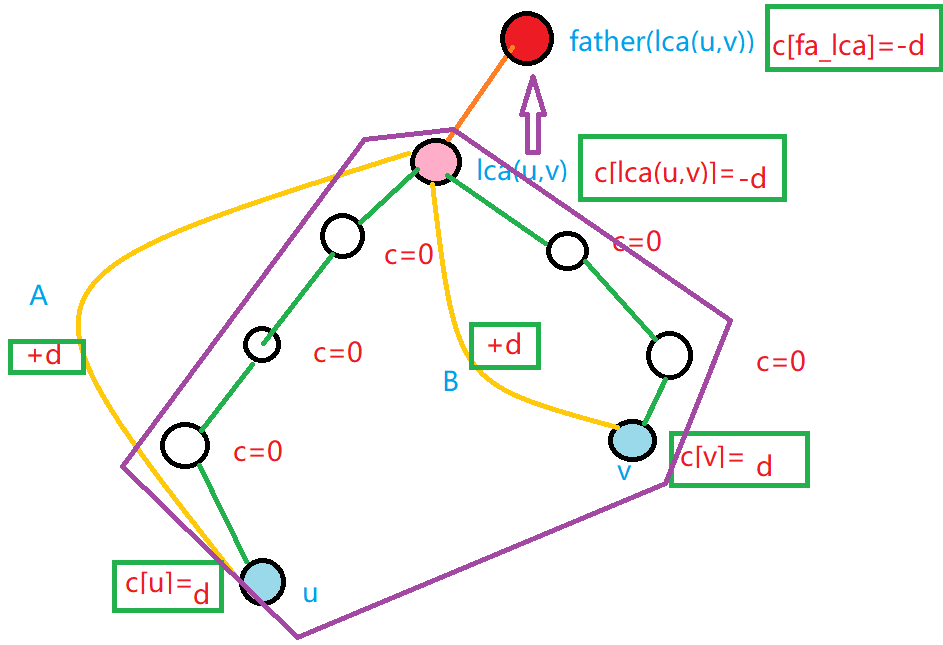
边差分

P3627 [APIO2009]抢掠计划 用了一个思想叫“点权化边权”，在这里反过来，“边权化点权”。

考虑任意的一条树边 \((u,v)\) ，一定满足它连接的是父亲和儿子。

那么这个边的“指向”就有唯一性，所以把每一条树边的权值压到它指向的“儿子节点”。

特别的，因为树根没有父亲，所以它的权值为 \(0\)

既然边权化点权了，那能不能直接跑点差分？

不行。

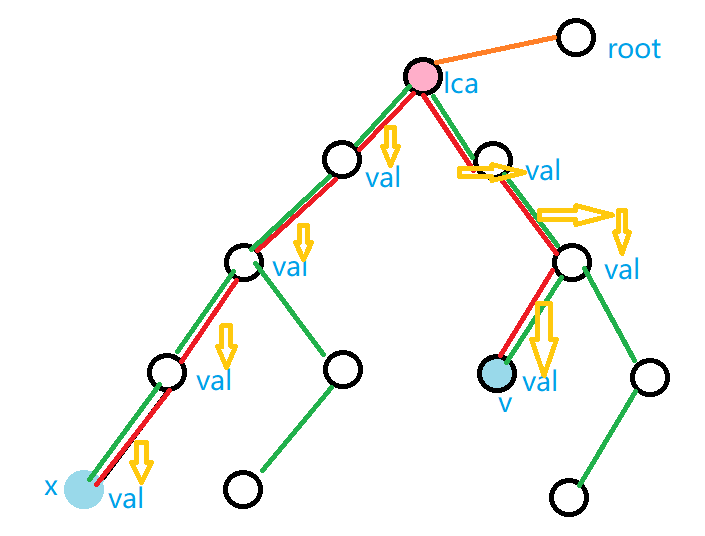
(\(u\) 打错成 \(x\)了）

注意到 \(\texttt{LCA}\) 的权值是 \(\delta(lca,root)\) 的权值，所以相当于是在跑一个去掉 \(\texttt{LCA}\) 的点差分。

于是就不需要考虑 \(\texttt{LCA}\) 的权值和它对 \(father({\texttt{LCA}})\) 的影响。

直接 \(c[u]+d,c[v]+d,c[lca]-2\times d\) 即可。

---

最后更新: May 9, 2023