CWOI 杂题选做(22Apr)

四月 Tricks 整理ψ(｀∇´)ψ

Acwing272 最长公共上升子序列ψ(｀∇´)ψ

求两个序列 \(a,b\) 的最长公共上升子序列的长度。

\(1\le n \le 3000\)

这题是 LIS 和 LCS 的综合。

首先考虑类似 LCS 设计这样一个状态： \(dp_{i,j}\) 表示 \(a[1 \sim i],b[1 \sim j]\) 构成的所有 LCIS，属性为 \(\max\)。

但是发现这样无法处理 “上升” 这一要素，所以考虑增加要素。

设 \(dp_{i,j}\) 表示 \(a[1 \sim i],b[1\sim j]\) 构成的，以 \(b_j\) 结尾的所有 LCIS，属性为 \(\max\)。

然后考虑划分 \(dp_{i,j}\) 这个子集。

类似 LCS 的划分方式，把 \(dp_{i,j}\) 划分成两个可以转移到它的部分：

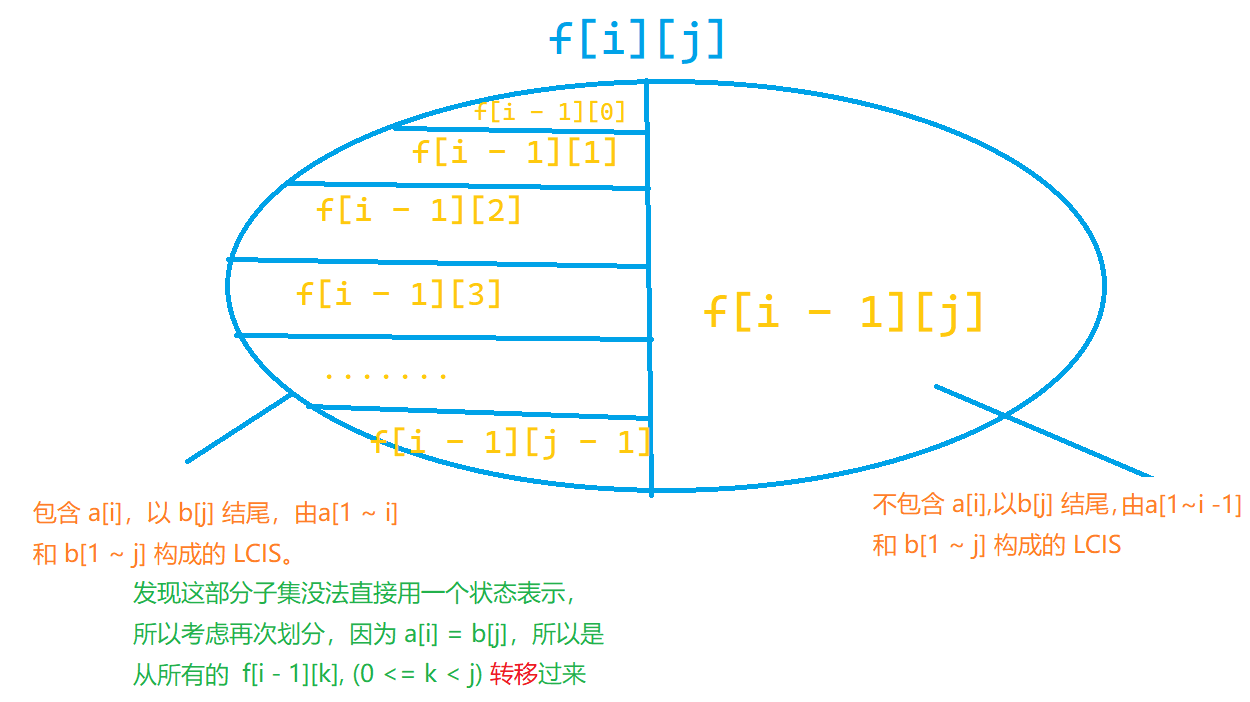
“包含 \(a_i\) 的由 \(a[1 \sim i],b[1\sim j]\) 构成的，以 \(b_j\) 结尾的所有 LCIS”。
“不包含 \(a_i\) 的由 \(a[1 \sim i],b[1\sim j]\) 构成的，以 \(b_j\) 结尾的所有 LCIS”。

第一种在 \(a_i = b_j\) 时转移，第二种在 \(a_i \not= b_j\) 时转移。

然后考虑用一个状态来分别表示。

第二个部分实际上是从 \(a[1 \sim i]\) 当中去除 \(a_i\)，所以是由 \(a[1 \sim i-1],b[i \sim j]\) 构成，以 \(b_j\) 结尾的 LCIS，可以用 \(dp_{i-1,j}\) 表示。

然后发现第一个部分找不到一个直接的状态来表示，所以继续划分。

首先因为 \(a_i = b_j\) ，所以子集的第一维不能取到 \(i\)，第二维不能取到 \(j\)。

而状态设计中，LIS 的要素体现在 “以 \(b_j\) 结尾”，所以考虑把这个子集用类似 LIS 的方式划分。

发现包含 \(a_i\)，以 \(b_j\) 结尾的 LCIS 都长成这样：

\[\begin{matrix}\dots,las_1,a_i/b_j \\ \dots,las_2,a_i/b_j\end{matrix}\]

发现 ”最后一个不同点“ 就是倒数第二个元素 \(las\)。

所以枚举 \(b\) 的上一个元素 \(las\)，即是把这个子集划分成 \(dp_{i-1,k},(0 \le k <j)\)。

（图中漏写了 ”所有“ 二字）

得到转移方程：

\[dp_{i,j} = \begin{cases}dp_{i-1,j} & a_i \not= b_j \\ \min\limits_{0 \le k < j}\{dp_{i-1,k}\} + 1 & a_i = b_j\end{cases}\]

发现方程是 \(\text{O}(n^3)\) 的，但是发现，当 \(i\) 固定的时候，\(j\) 增加 \(1\) ，那么 \(dp_{i-1,k}\) 的“候选集合”只会增加一个元素 \(dp_{i-1,j-1}\)。

而此处求得是“候选集合”当中的最小值，所以可以直接拿一个变量记录当前的候选集合的最小值，直接利用这个变量转移即可。

Code

f[0][0] = a[0] = b[0] = 0;
for(int i = 1; i <= n; ++i) {
    int cand = 0;
    if(b[0] < a[i]) cand = f[i - 1][0]; // 初始在决策候选集合中的数。
    for(int j = 1; j <= n; ++j) {
        if(a[i] == b[j]) 
            f[i][j] = cand + 1;
        else
            f[i][j] = f[i - 1][j];
        if(b[j] < a[i]) cand = max(cand, f[i - 1][j]);
    }
}
int res = 0;
for(int i = 1; i <= n; ++i) {
    res = max(f[n][i], res);
}

Tricks

如果划分状态集合的时候，发现当前集合无法使用一个状态直接表示，可以尝试继续划分或者添加要素。
如果用于 “决策” 的 “候选集合” 在外层循环固定，内层循环增加时元素个数 “只增多不减少”，可以考虑直接使用一个变量记录最优决策。
不管是不是正解，先打出正确的部分分暴力，再考虑是否可以优化成更优的解法。

Tag : DP/LCS

Acwing274 Mobile serviceψ(｀∇´)ψ

一个公司有三个移动服务员，最初分别在位置 \(1，2，3\) 处。

如果某个位置（用一个整数表示）有一个请求，那么公司必须指派某名员工赶到那个地方去。

某一时刻只有一个员工能移动，且不允许在同样的位置出现两个员工。

从 \(p\) 到 \(q\) 移动一个员工，需要花费 \(c(p,q)\)。

这个函数不一定对称，但保证 \(c(p,p)=0\)。

给出 \(N\) 个请求，请求发生的位置分别为 \(p_1 \sim p_N\)。

公司必须按顺序依次满足所有请求，且过程中不能去其他额外的位置，目标是最小化公司花费，请你帮忙计算这个最小花费。

\(1\le L \le 200, 1\le N \le 3000\)。

首先考虑一个最简单的状态设计：设 \(dp_i\) 表示处理完前 \(i\) 个请求，公司的最小花费。

但是这样根本无法转移，因为不知道每个员工上一个位置在哪里。

所以考虑添加额外的维度来记录三个员工的位置。

设 \(dp_{i,x,y,z}\) 表示处理完前 \(i\) 个请求，第一二三个员工分别在 \(x,y,z\) 处，公司当前的最小花费。

然后考虑对这个状态集合进行划分。

因为状态是“处理完”，所以当前知道的信息是最终的位置，不便于找出上一个位置。

所以可以考虑不是从 \(i - 1\) 转移到当前状态，而是从当前状态顺推更新 \(i+1\)。

枚举每一个员工去处理 \(p_{i+1}\) 的情况即可。

但是转移之前要判合法性，要求 \(x \not=y\not=z\)。

但是这样空间明显会爆炸，考虑优化。

因为处理完 \(p_i\) 之后，在合法的状态下，\(x,y,z\) 当中必然有一个等于 \(p_i\)。

所以可以省去一维，设 \(dp_{i,x,y}\) 表示其中一个位于 \(p_i\)，另外两个位于 \(x,y\) 。

然后用类似的方式转移即可。

Code

memset(dp, 0x3f, sizeof dp);
dp[0][1][2] = 0, p[0] = 3;
for(int i = 0; i <= n; ++i) {
    for(int x = 1; x <= l; ++x) {
        for(int y = 1; y <= l; ++y) {
            if(x == y || x == p[i] || y == p[i]) continue;
            dp[i + 1][x][y] = min(dp[i + 1][x][y], dp[i][x][y] + c[p[i]][p[i + 1]]);
            dp[i + 1][p[i]][y] = min(dp[i + 1][p[i]][y], dp[i][x][y] + c[x][p[i + 1]]);
            dp[i + 1][x][p[i]] = min(dp[i + 1][x][p[i]], dp[i][x][y] + c[y][p[i + 1]]);
        }
    }
}
int res = 0x3f3f3f3f;
for(int x = 1; x <= l; ++x) {
    for(int y = 1; y <= l; ++y) {
        if(x == y || x == p[n] || y == p[n]) continue;
        res = min(res, dp[n][x][y]);
    }
}
cout << res << endl;

本题的转移方式相当于求当前集合是哪几个状态的子集，然后把当前集合转移到对应的大集合中。

Tricks

当 “阶段” 类的信息维度无法表示当前状态，或者无法进行划分转移时，可以考虑添加额外的信息维度。
** 当 “阶段” 总是从一个阶段转移到下一个阶段，可以不用管附加信息维度的大小变化情况，因为无后效性已经由阶段解决了。
** 如果选择的信息维度过多，可以考虑检查它们是否可以通过某种方式相互得到，比如本题，知道另外两个员工的位置，就一定能知道另外一个员工的位置，所以只需要两个员工的位置信息即可覆盖整个状态空间。

Tag : DP

Acwing284 金字塔ψ(｀∇´)ψ

金字塔由若干房间组成，房间之间连有通道。

如果把房间看作节点，通道看作边的话，整个金字塔呈现一个有根树结构，节点的子树之间有序，金字塔有唯一的一个入口通向树根。

并且，每个房间的墙壁都涂有若干种颜色的一种。

机器人会从入口进入金字塔，之后对金字塔进行深度优先遍历。

机器人每进入一个房间（无论是第一次进入还是返回），都会记录这个房间的颜色。

最后，机器人会从入口退出金字塔。

显然，机器人会访问每个房间至少一次，并且穿越每条通道恰好两次（两个方向各一次），然后，机器人会得到一个颜色序列 \(S\)。

但是，探险队员发现这个颜色序列并不能唯一确定金字塔的结构。

现在他们想请你帮助他们计算，对于一个给定的颜色序列，有多少种可能的结构会得到这个序列。

因为结果可能会非常大，你只需要输出答案对\(10^9\) 取模之后的值。

\(|S| \le 3000\)

看到这种类 DFS 序，不难想到一个 Trick：一颗子树内的 DFS 序必然连续，这种类 DFS 序也是一样。

发现问题是由多少种可能序列，所以不难想到一个区间 DP 的状态：

设 \(dp_{l,r}\) 表示 \(S_{l\sim r}\) 这一段颜色序列表示的子树所有可能的结构方案，属性为数量。

可以发现，\(dp_{l,r}\) 是合法状态，当且仅当 \(r-l+1 \equiv1(\operatorname{mod} 2)\) 且 \(S_l = S_r\)。

先排除掉所有不合法的状态，即是循环时 \(len = 1,3,5,\dots\)。

然后可以发现，\(S_l,S_r\) 代表的节点必然是同一个，就是这段 DFS 序连续的子树的根（进去再出来）。

那么一个经典的根据乘法原理的计数法就是，枚举这个节点的所有儿子节点，将以儿子节点为根的子树的 DP 值全部乘起来得到当前的答案。

只需要枚举所有划分点的位置 \(k\)，

但是这样复杂度上天，必然不可行。

用区间 DP 的 ”合并类“ 惯用套路可以想到另外一个做法，枚举划分点 \(k\)，

那么左边和右边都可能是若干颗子树，但是这样子是会算重的，因为你不知道这几颗子树是不是能重新排列一下变成新的子树。

所以此时要用到区间 DP ”划分类“的思想，用前一段的状态和后一段的花费得到整段的状态。

具体来说，我们需要控制划分成两个部分的后一个部分只包含一棵子树。

所以枚举 \(k\)。

保证 \(S_l = S_r = S_k\) 且 \(k - l + 1 \equiv r - (k + 1) - 1 \equiv 1 (\operatorname{mod}2)\)。

则 \(dp_{l,k}\) 是一个已经计算好的状态，后一段是一棵由 \(S_{k+1}\sim S_{r-1}\) 构成的子树。

那么令 \(dp_{l,r}\) 加上 \(dp_{l,k} \times dp_{k + 1,r-1}\) 即可。

Code

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int si = 3e2 + 10;
constexpr int mod = 1e9;

int n;
string s;
int dp[si][si];

int main() {
    cin >> s;
    int n = (int)s.size();
    s = ' ' + s;
    if(!(n & 1)) return puts("0"), 0;

    memset(dp, 0, sizeof dp); // 状态不合法或者未更新时，dp = 0。
    for(int i = 1; i <= n; ++i)
        dp[i][i] = 1;

    for(int len = 3; len <= n; len += 2) {
        for(int i = 1; i + len - 1 <= n; ++i) {
            int j = i + len - 1;
            if(s[i] != s[j]) continue;
            for(int k = i; k <= j - 2; k += 2) {
                if(s[k] == s[j])
                    dp[i][j] = (dp[i][j] + 1ll * dp[i][k] * dp[k + 1][j - 1] % mod) % mod;
            }
        }
    }

    cout << dp[1][n] % mod << endl;
    return 0;
}

Tag : 区间DP/DFS序

Acwing288 休息时间ψ(｀∇´)ψ

在某个星球上，一天由 \(N\) 个小时构成，我们称 \(0\) 点到 \(1\) 点为第 \(1\) 个小时、\(1\) 点到 \(2\) 点为第 \(2\) 个小时，以此类推。

在第 \(i\) 个小时睡觉能够恢复 \(U_i\) 点体力。

在这个星球上住着一头牛，它每天要休息 \(B\) 个小时。

它休息的这 \(B\) 个小时不一定连续，可以分成若干段，但是在每段的第一个小时，它需要从清醒逐渐入睡，不能恢复体力，从下一个小时开始才能睡着。

为了身体健康，这头牛希望遵循生物钟，每天采用相同的睡觉计划。

另外，因为时间是连续的，即每一天的第 \(N\) 个小时和下一天的第 \(1\) 个小时是相连的（\(N\) 点等于 \(0\) 点），这头牛只需要在每 \(N\) 个小时内休息够 \(B\) 个小时就可以了。

请你帮忙给这头牛安排一个睡觉计划，使它每天恢复的体力最多。

\(3 \le N \le 3830, 2 \le B < N\)

这是一个环形问题，但是不同于其它的处理方式，它并不是断环成链。

先当作一个线性问题思考。

观察题目要素，发现呈 “阶段” 出现的就是 “时间” 这一维度，所以先设 \(dp_i\) 表示考虑前 \(i\) 个小时（时间段）的什么东西。

然后发现关乎决策的要素是类似背包中”体积“的一个信息： ”休息的时间“。

所以加一维，\(dp_{i,j}\) 表示考虑前 \(i\) 个小时，已经休息了 \(j\) 个小时的所有方案，属性为获得体力的最大值。

但是这样无法转移，因为还有一个要素没用进去，”睡觉的第一个时间段不能恢复体力“。

所以还需要知道牛上一个小时睡没睡，才能确定从哪里开始，牛是在睡第一个小时。

那么再加一维，设 \(dp_{i,j,0/1}\) 表示考虑前 \(i\) 个小时，已经休息了 \(j\) 个小时，第 \(i\) 个小时是否在睡觉的所有方案。

分开讨论 \(0/1\) ，并在转移带上要素：”睡觉的第一个时间段不能恢复体力“。

所以可以得到方程：

\[\begin{cases}dp_{i,j,0} = \max(dp_{i-1,j,0},dp_{i-1,j,1}) \\ dp_{i,j,1} = \max(dp_{i-1,j-1,0},dp_{i-1,j-1,1}+U_i)\end{cases}\]

然后这个空间有点大，算一下之后发现过不了。

又发现每一个阶段之和上一个阶段 \(i-1\) 有关，所以可以滚动数组，也就是利用 \(i\&1\) ，在 \(dp_0,dp_1\) 两个系之间不断转移。

然后环形怎么处理呢？发现这样子做是无法考虑到时刻 \(1\) 可以获取体力的情况的，因为这是个环，

所以我们强制选上 \(U_1\)，也就是令 \(dp_{1,1,1} = U_1\)，然后再跑一次就行了，这是处理环形DP，除了断环成链以外的另一种方法。

Code

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int si = 3830 + 10;

int n, m;
int a[si];
int dp[2][si][2];

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; ++i) 
        cin >> a[i];

    // for(auto x : a) cout << x << " ";
    // cout << endl;

    memset(dp, -0x3f, sizeof dp);
    dp[1][0][0] = 0, dp[1][1][1] = 0;

    for(int i = 2; i <= n; ++i) {
        dp[i & 1][0][0] = 0;
        for(int j = 1; j <= i; ++j) {
            dp[i & 1][j][0] = max(dp[(i - 1) & 1][j][0], dp[(i - 1) & 1][j][1]);
            dp[i & 1][j][1] = max(dp[(i - 1) & 1][j - 1][0], dp[(i - 1) & 1][j - 1][1] + a[i])  ;
        }
    } 

    int ans = max(dp[n & 1][m][0], dp[n & 1][m][1]);

    memset(dp, -0x3f, sizeof dp);
    dp[1][1][1] = a[1];

    for(int i = 2; i <= n; ++i) {
        dp[i & 1][0][0] = 0;
        for(int j = 1; j <= i; ++j) {
            dp[i & 1][j][0] = max(dp[(i - 1) & 1][j][0], dp[(i - 1) & 1][j][1]);
            dp[i & 1][j][1] = max(dp[(i - 1) & 1][j - 1][0], dp[(i - 1) & 1][j - 1][1] + a[i])  ;
        }
    } 

    ans = max(ans, dp[n & 1][m][1]);

    cout << ans << endl;
    return 0;
}

Tag : DP/环形处理

Acwing315 旅行ψ(｀∇´)ψ

求 LCS 的所有可能方案。

首先求出 \(dp_{i,j}\)，然后考虑如何统计方案。

发现只需要找到的最后一个相同的位置。

所以计算出 \(lasa[ch][i],lasb[ch][i]\)，分别表示 \(ch\) 在 \(a/b\) 的前 \(i\) 位最后出现的位置。

然后设一个函数 \(f(x,y,rest)\)，表示当前处理到 \(a[1\sim x],b[1\sim y]\)，LCS 长度还剩 \(rest\)。

先判掉边界，然后枚举 \(26\) 个字符，看 \(dp_{lasa[ch][i],lasb[ch][j]}\) 是否等于 \(rest\)，如果是的话，执行 \(f(lasa[ch][i],lasb[ch][j],rest-1)\) 即可。

记得在 \(f\) 里开一个 std::string 的 member 去记录当前情况的字符串，当 \(rest = 0\) 时，把这个字符串放入一个 std:vector。

Code

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int si = 1e2 + 10;

int n, m;
string a, b;

int dp[si][si];
int lasa[27][si], lasb[27][si];

vector<string> res; 

void print(int i, int j, int rest, string cur) {
    if(rest == 0) {
        res.push_back(cur);
        return;
    }

    if(!i || !j) return;

    for(int ch = 1; ch <= 26; ++ch) {
        int prei = lasa[ch][i], prej = lasb[ch][j];
        if(dp[prei][prej] == rest)
            print(prei - 1, prej - 1, rest - 1, (char)('a' + ch - 1) + cur);
    }
}

int main() {
    cin >> a >> b;
    n = (int)a.size(), m = (int)b.size();
    a = ' ' + a, b = ' ' + b;

    memset(dp, 0, sizeof dp);
    memset(lasa, 0, sizeof lasa);
    memset(lasb, 0, sizeof lasb);

    for(int i = 1; i <= n; ++i) {
        for(int j = 1; j <= m; ++j) {
            if(a[i] == b[j]) 
                dp[i][j] = dp[i - 1][j - 1] + 1;
            else 
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
        }
    }

    // cout << dp[n][m] << endl;

    for(int i = 1; i <= n; ++i) {
        for(int ch = 1; ch <= 26; ++ch) {
            if(a[i] == (char)('a' + ch - 1))
                lasa[ch][i] = i;
            else 
                lasa[ch][i] = lasa[ch][i - 1];
        } 
    }
    for(int i = 1; i <= m; ++i) {
        for(int ch = 1; ch <= 26; ++ch) {
            if(b[i] == (char)('a' + ch - 1))
                lasb[ch][i] = i;
            else 
                lasb[ch][i] = lasb[ch][i - 1];
        }
    }

    print(n, m, dp[n][m], "");
    sort(res.begin(), res.end());

    for(auto x : res) 
        cout << x << endl;

    return 0;
}

Tag : DP/LCS的方案

Acwing322 消木块ψ(｀∇´)ψ

\(n\) 个木块排成一列，每个木块都有一个颜色。

每次，你都可以点击一个木块，这样被点击的木块以及和它相邻并且同色的木块就会消除。

如果一次性消除了 \(k\) 个木块，那么就会得到 \(k\times k\) 分。

给定你一个游戏初始状态，请你求出最高得分是多少。

\(1\le N \le 200\)。

首先考虑区间 DP，设 \(dp_{l,r}\) 表示删去 \([l,r]\) 这个区间的所有木块所能得到的最大得分。

可以考虑枚举中间点，然后用两段的状态合并得到大一点的状态。

但是如果遇到这种情况：[...1 1 1][1 1 1...]

你如果从中间分开，那么 \(3^2+3^2 < 6^2\)，必然不是更优的，你需要让尽可能多的同色木块被放在一起合并。

所以我们考虑类似 ODT 的思想，将所有的初始同色的木块合成一段，这样就能避免以上的情况。

但是我们又不好转移这一种情况：[2 2 2] [1 1] [3] [2 2 2],

假设你用这两个状态合并：\(dp_{1,3}\) 和 \(dp_{4,4}\)。

那你删完了 \(1,2,3\) 段之后，把 \(1\) 这一段 \(2\) 都删掉了，使得它无法和 \(4\) 这一段的 \(2\) 合并。

并且可以发现，你如果只枚举一个划分点，肯定无法使得上面的情况更优。

所以考虑枚举所有划分点，但是这样子复杂度多了 \(2^n\) 的指数级别，无法接受。

但是发现，任意一种颜色的最优决策之间是相互独立的，你要删也只会删掉同种颜色。

所以我们可以考虑加一维状态：\(dp_{i,j,k}\) 表示删掉区间 \([i,j]\)，并且 \(j\) 后面有 \(k\) 个和第 \(j\) 段同种颜色的木块，能得到的最大得分。

为啥不是段而是个呢？

如果是这样的情况：[1 1 1] [2] [3 3] [2]<--|j| [4] [2 2] [5] [2]。

你后面可以和 \(j\) 合并的有 \(3\) 个 \(2\)，如果你直接设 \(k\) 为段数的话，还要知道每一段分别有多少个，复杂度又会上去。

首先可以让 \(dp_{i,j,k}\) 等于直接删除 \(j\) 和后面所有与 \(j\) 颜色相同块的方案 \(dp_{i,j-1,0}+(len_j+k)^2\)。

也就是直接删除 \([i,j)\)，然后和 \(j\) 一起删除后面的 \(k\) 个。

但是如何保证能让这 \(k\) 个连到一起呢？你要先把分开他们的删除了才行啊。

前面提到，不同种颜色的决策之间是相互独立的，所以中间相隔的那些，因为区间长度更小，必然会在枚举当前状态之前就被意义上“删除了”，并且得到一个分数。

那实际上转移的时候就可以当作没有这些相隔的元素了。

然后还要考虑 \([i,j)\) 中也有和第 \(j\) 段颜色相同的段（上面列举的情况中的第 \(2\) 段那一个 \(2\)），一起和 \(j\)，还有后面的 \(k\) 个删除的情况。

此时 \(j\) 也会被考虑到这一段的 “\(k\)” 当中，所以还需要删除 \((l,j)\)。

这个枚举满足 \(color_l = color_j\) 的 \(l\) 即可。

这部分的转移是：

\[dp_{i,j,k} = \max(dp_{i,j,k},dp_{i,l,len_j + k} +dp_{l + 1, j - 1, 0})\]

写记忆化搜索即可，得到代码：

Code

int sqr(int x) {return x * x;}

int dp(int l, int r, int ex) {
    if (r < l) return 0;
    if (f[l][r][ex] != -1) return f[l][r][ex];
    int ans = dp(l, r - 1, 0) + sqr(len[r] + ex);
    for (int i = l; i < r; ++i)
        if (a[i] == a[r])
            ans = max(ans, dp(l, i, len[r] + ex) + dp(i + 1, r - 1, 0));
    return f[l][r][ex] = ans;
}

答案是 \(dp(1,n,0)\)。

这题启发了我们一个 Trick：

Trick

当遇到区间 DP 删除完一个区间后，会导致这个区间两边构成更优决策的情况时，一般考虑对区间两边可能能构成最优决策的状态进行状态的记录和转移。

下一道题也是一样的 Trick。

Tag : 区间DP/区间删除类DP

*CF607B Zumaψ(｀∇´)ψ

和上一道一起总结。

咕咕咕

*Acwing281 Coinsψ(｀∇´)ψ

多重背包优化DP，可行性。

咕咕咕

最后更新: May 9, 2023