Kruskal 重构树

泛化ψ(｀∇´)ψ

假设我们正在使用 Kruskal 求最小生成树。

可以注意到我们会按照边权从小到大的顺序加入若干条边。

有一种结构可以利用这个性质拓展出很多好用的性质，被称为 Kruskal 重构树。

构建的方法大概是：在 Kruskal 每次合并两个集合 \(S_u, S_v\) 的时候，新建一个虚拟节点作为 \(u, v\) 的父亲，父亲节点的权值为连通这两个集合的最小边权（也就是 Kruskal 的过程中加入进来的边）。

然后可以得到这样的一棵树：

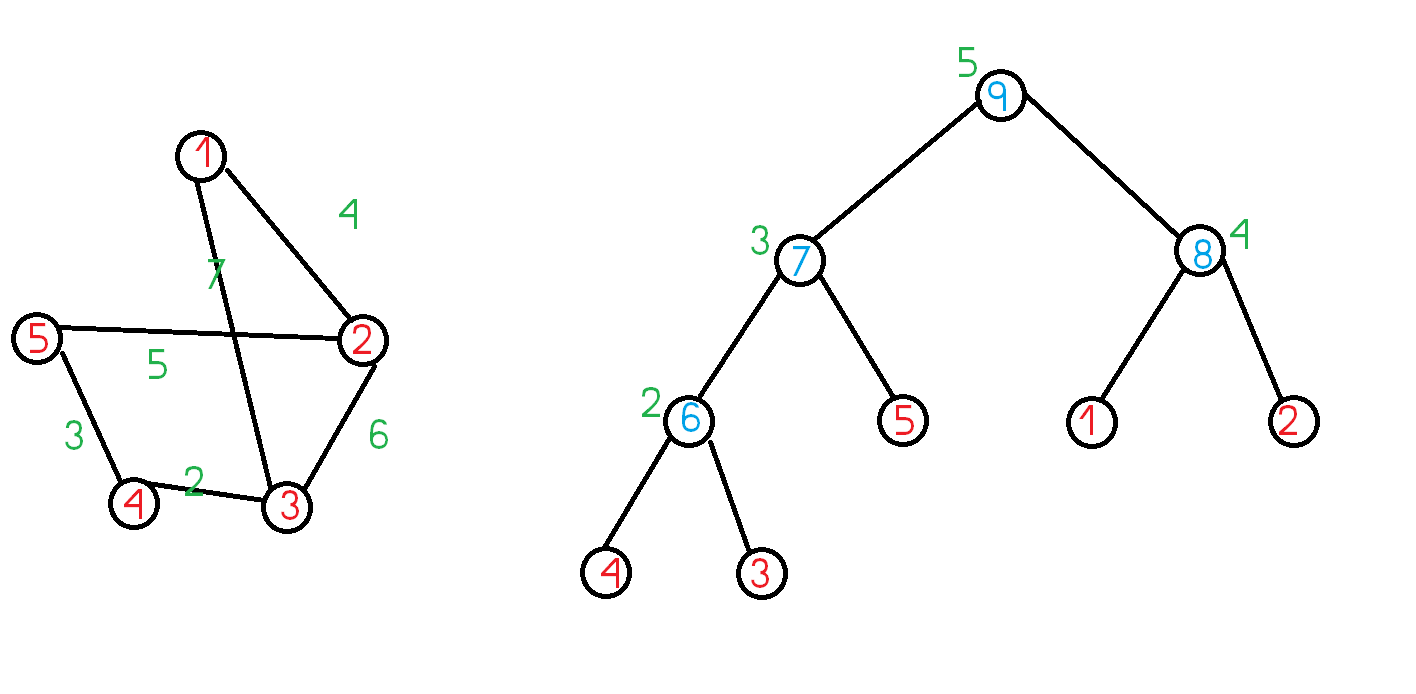
可以直观地看出它具有如下的一些性质：

有 \(2n - 1\) 个节点（\(n\) 个原来的节点，和 \(n-1\) 个对应生成树的边的虚拟节点）
它是一颗完全二叉树，并且点权符合大根堆的性质（假设叶子节点点权为 \(+\infty\)）。

还有一些不太容易看出来的性质：

对于两个原图上的节点 \(u, v\)，他们之间的所有路径中最大边的最小值为它们在重构树上的 LCA 的点权，同样也是它们之间在最小生成树上的简单路径上的边权最大值。
由 2，3 可以推广出，到 \(x\) 的所有路径中最大边的最小值 \(\leq val\) 的所有节点都为重构树上某个节点子树中的叶子节点，这个节点就是 \(x\) 到重构树树根的路径上，深度最浅的节点.

3 这个性质其实不难理解，我们只需要考虑 Kruskal 求 mst 的过程，我们每次会选择一条边加入，如果两个节点仅有一条边相连，那么这个性质显然成立，如果中间隔了一个节点，那么它会先选中小边，再选中大边，可以发现，让这两个节点联通的最后一条边一定是这条路径上边权最大的，显然这条路径就是 mst 上的这两点之间的简单路径，那么也就是最大边的最小值了，推广下就是性质 3 了。

例题ψ(｀∇´)ψ

这个最经典的显然就是【NOI2018 归程】吧，SPFA 死了那个题。

做法是简单的。

注意到我们想知道每次询问，哪些节点是可以直接开车到大的。

这个限制就非常 Kruskal 重构树，我们考虑对海拔建最大生成树，然后倍增按照性质 4 找到一个节点 \(u\)，其中 \(val \le p\)。

然后这个子树内的叶子都可以作为下车点，特判一下 \(1\) 在不在子树里，不在就求一下每个点到根的最短路，然后求一个子树 min 就行了。

子树 min 这个可以在建重构树的时候直接维护，复杂度 \(O((n + m + q) \log n)\)。

代码我摆了，随便贺了一份。

最后更新: September 27, 2023