DFS 序相关
dfs 序ψ(`∇´)ψ
此处说的 dfs 序是访问到这个节点的时间戳 dfn。
最重要的性质就是,子树内的 dfn 是连续的一段区间。
所以可以用于子树的操作和询问。
括号序ψ(`∇´)ψ
dfs,进入某个节点的时候记录一个左括号 (,退出某个节点的时候记录一个右括号 )。
每个节点会出现两次。相邻两个节点的深度相差 1。
这个东西必然是一个合法括号序列,并且一个节点对应的配对的一对括号之内可以代表这个节点的子树。
树上莫队会用到。
欧拉序ψ(`∇´)ψ
之后补。
dfs 树ψ(`∇´)ψ
这里是无向图的 dfs 树。
横叉边的定义和关于连通性的 tarjan 算法里面一样。
回边就是连通 dfs 树上节点和祖先节点的一条非 dfs 树边。
有一个重要的性质:
无向简单连通图 \(G\) 的非 dfs 树边,都不是横叉边(全部都是回边)。
Proof:
证明:假设有一条边 \(u \to v\),dfs 已经访问过了 \(u\) 但还没访问到 \(v\)。
然后会有两种情况,
如果沿着 \(u\to v\) 这条边,dfs 由 \(u\) 去向 \(v\),那么 \(u\to v\) 就是一条树边。
如果深度优先遍历没有沿着 \(u\to v\) 这条边从 \(u\) 走到 \(v\),
那么证明最后访问到 \(v\) 的时候,是从 \(u\) 出发走了另外一条路径,然后再到 \(v\) 的。
所以 \(v\) 就一定是 \(u\) 的一个子孙节点,\(u\to v\) 就是一条回边。
可以看一看来自 https://codeforces.com/blog/entry/68138 的一张图理解一下:
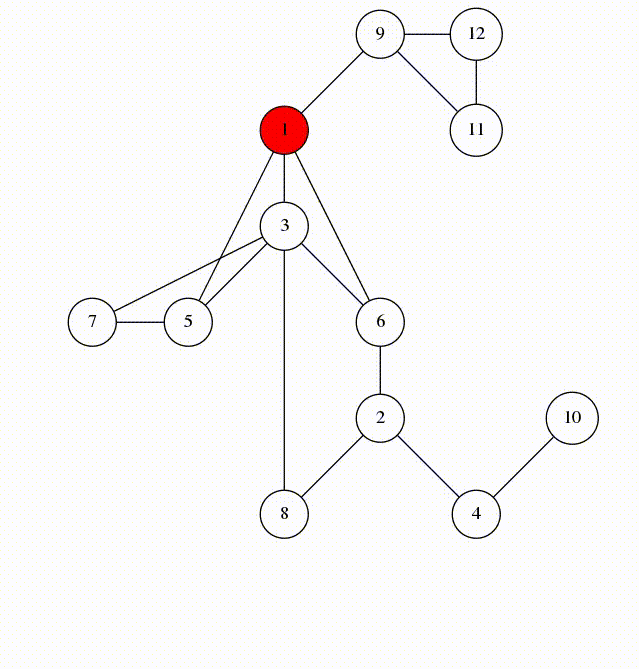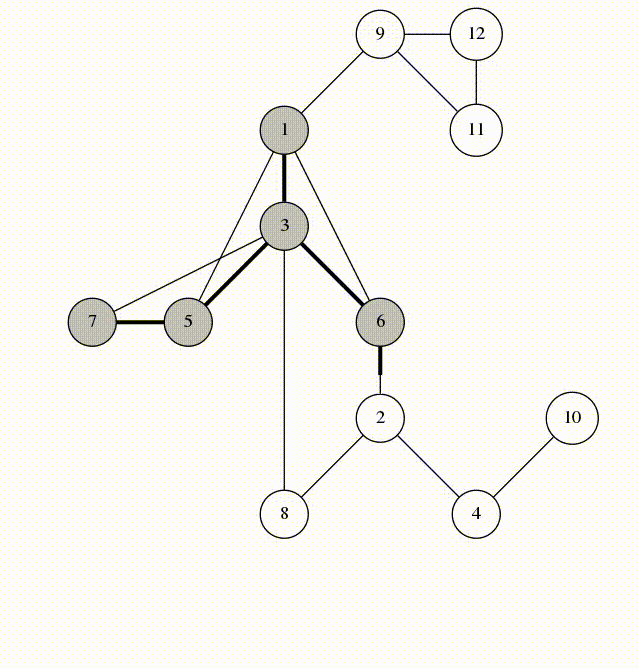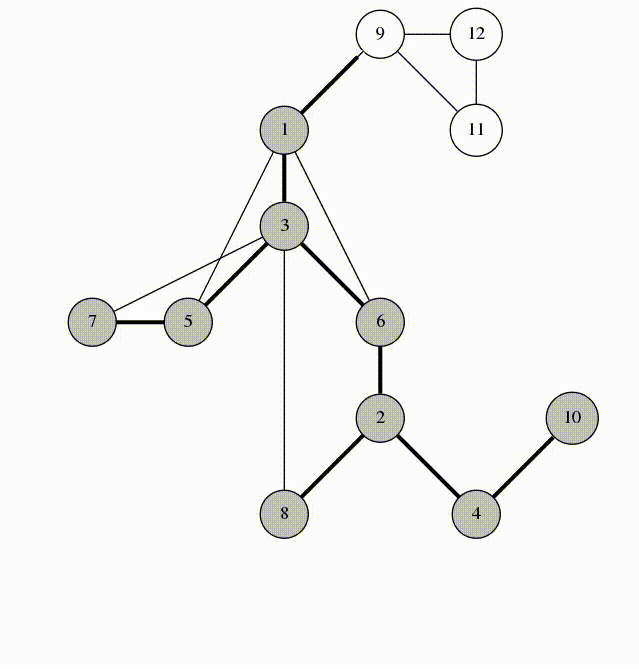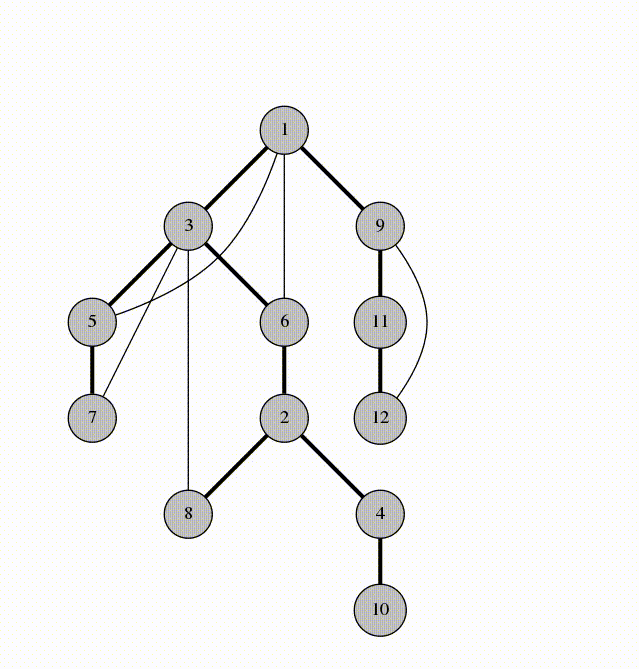
bfs 树ψ(`∇´)ψ
这里是无向图的 bfs 树。
有一个重要的性质:
无向简单连通图 \(G\) 的非 bfs 树边,都是横叉边(全部都不是回边)。
且这些边连接的节点的层数差的绝对值小于等于 \(1\)。
Proof:
我们可以类比 dfs 树那里的过程。
考虑存在一条边 \(u \to v\),并且此时已经访问过了 \(u\),没有访问 \(v\).
那么会有以下的量种情况:
1:如果沿着 \(u \to v\) 这条边访问了 \(v\),那么 \(u \to v\) 就是树边。
2:如果没有沿着 \(u \to v\) 这条边访问 \(v\),因为 bfs 是按层扩展的,所以 \(u\) 的下一次必然会扩展到 \(v\)。
但是 \(v\) 没有通过 \(u\) 扩展到,所以第一种可能就是它是和 \(u\) 同层的节点,被同时扩展过。
也有一种可能是 \(u\) 确实能扩展到 \(v\),但是和 \(u\) 同层的某个节点也能扩展到 \(v\),那么 \(u\) 就没法扩展到 \(v\)。
最后的一种可能是 \(v\) 是 \(u\) 的上层节点,这是不可能出现的,因为这样的话肯定是 \(v\) 先被扩展到。
所以绝对值的结论可以用情况 2 的第一二种可能证明,其他的可以用来证明横叉边的结论。