前缀和 & 差分

前缀和

一维前缀和

可以实现 \(\text{O}(n)\) 预处理，\(\text{O}(1)\) 询问区间和。

令 \(sum_i\) 表示区间 \([0,i]\) 的前缀和。

特别的，\(a_0=0\)。

那么每次累加即可，查询区间 \([l,r]\) 的和只需要输出 \(sum_r-sum_{l-1}\)。

int a[si],sum[si]; a[0]=sum[0]=0;
for(register int i=1;i<=n;++i){
    scanf("%d",&a[i]),sum[i]=sum[i-1]+a[i];
} int l,r; scanf("%d%d",&l,&r),printf("%d\n",sum[r]-sum[l-1]);

二维前缀和

可以实现 \(\text{O}(n^2)\) 预处理，\(\text{O}(1)\) 询问矩阵和。

令 \(sum_{i,j}\) 表示左上角为 \((1,1)\) ，右下角为 \((i,j)\) 的矩阵和。

考虑容斥，预处理的时候令 \(sum_{i,j}=sum_{i-1,j}+sum_{i,j-1}-sum_{i-1,j-1}+a[i][j]\)。

仍然考虑容斥，询问左上角为 \((x_1,y_1)\) ，右下角为 \((x_2,y_2)\) 的子矩阵则只需要：

\(ans=sum_{x_2,y_2}-sum_{x_1 - 1,y_2}-sum_{x_2,y_1 - 1}+sum_{x_1 - 1,y_1 - 1}\) 。

int a[si][si],sum[si][si];
memset(sum,0,sizeof sum);
for(register int i=1;i<=n;++i){
    for(register int j=1;j<=m;++j){
        scanf("%d",&a[i][j]),sum[i][j]+=a[i][j];
    }
}
for(register int i=1;i<=n;++i){
    for(register int j=1;j<=m;++j){
        sum[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
    }
}
int x,xx,y,yy; scanf("%d%d%d%d",&x,&y,&xx,&yy);
printf("%d\n",sum[xx][yy]-sum[x-1][yy]-sum[xx][y-1]+sum[x-1][y-1]);

差分

一维差分

可以实现 \(\text{O}(1)\) 修改，\(\text{O}(n)\) 查询。

一个便于理解的特点就是，原数组就是差分序列的前缀和。

定义差分序列 \(c_i=\begin{cases}a_1 & i=1 \\ a_i-a_{i-1} & \text{otherwise.}\end{cases}\)

然后如果要修改 \([l,r]\) ，那么给 \(c[l]\) 加上 \(d\)，\(c[r+1]\) 减去 \(d\) 。

其实很好理解，要让 \(c\) 的前缀和数组的 \([l,r]\) 改变，那先在 \(l\) 这儿加上 \(d\) ，让 \(a[l]\to a[n]\) 都多一个 \(d\) 。

然后在 \(r+1\) 这儿减去 \(d\) ，让 \(a[r+1] \to a[n]\) 都少一个 \(d\) 就可以了。

int a[si],c[si];
scanf("%d",&a[1]),c[0]=0,c[1]=a[1];
for(register int i=2;i<=n;++i){
    scanf("%d",&a[i]),c[i]=a[i]-a[i-1];
} int l,r,d; scanf("%d%d%d",&l,&r,&d),c[l]+=d,c[r+1]-=d;
for(register int i=1;i<=n;++i){
    c[i]+=c[i-1],printf("%d\n",c[i]);
} // 做前缀和恢复序列。

二维差分

可以实现 \(\text{O}(1)\) 修改， \(\text{O}(n^2)\) 查询。

定义差分矩阵 \(c_{i,j}\) ，满足 \(a_{i,j}\) 为 \(c_{i,j}\) 的前缀和矩阵。

用二维前缀和的思想可以得到：

\(a_{i,j}=a_{i-1,j}+a_{i,j-1}-a_{i-1,j-1}+c_{i,j}\)。

那么 \(c_{i,j}=a_{i,j}-a_{i-1,j}-a_{i,j-1}+a_{i-1,j-1}\)。

然后考虑怎么样进行矩阵维护。

类似一维差分的思想，我打算在端点处进行维护。

比如给 \((x_1,y_1)\) 为左上角，\((x_2,y_2)\) 为右下角的子矩阵全部加上 \(d\) ，可以用二维线段树，但是这里考虑差分。

首先尝试给 \(c_{x_1,y_1}\) 加上 \(d\) ，那么发现从 \((x_1,y_1)\) 一直到整个矩阵的右下角都被加了 \(d\) ，然后我们又需要保留 \((x_1,y_1) \to (x_2,y_2)\)。

那么用容斥思想，让 \(c_{x_1,y_2+1}\)，和 \(c_{x_2+1,y_1}\) 全部减去 \(d\) ，然后发现有个部分被多减去了，是 \(c_{x_2+1,y_2+1}\)，所以给它加回来。

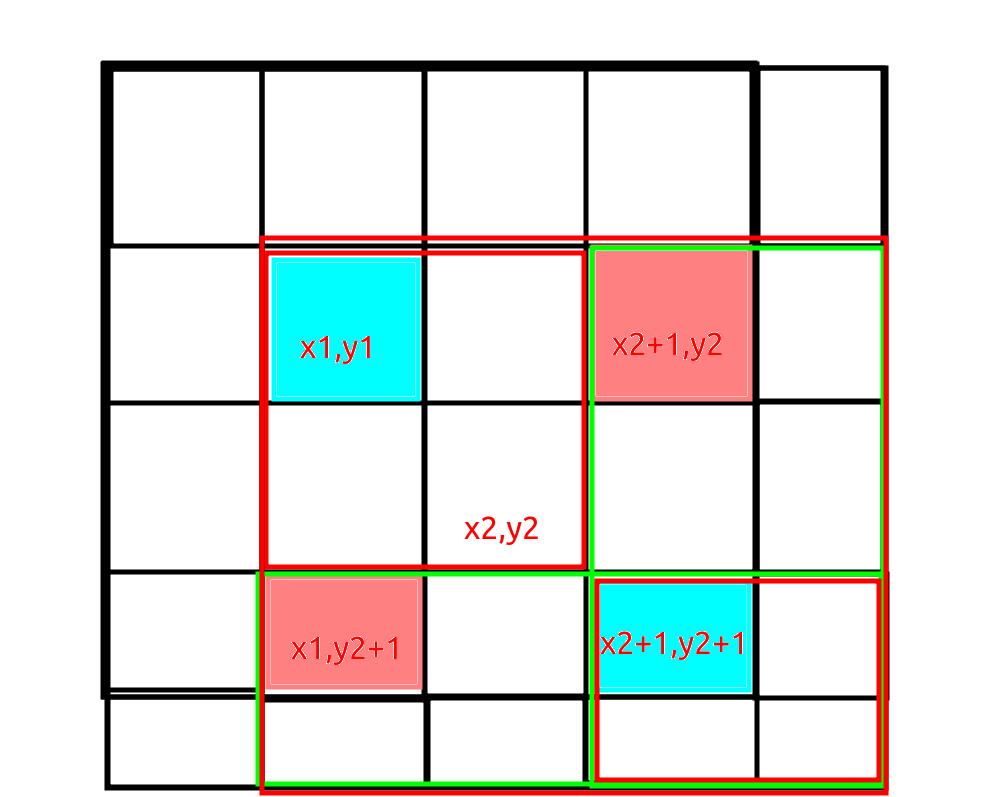
那么修改就化为了四步。

int a[si][si],c[si][si];
for(register int i=1;i<=n;++i){
    for(register int j=1;j<=m;++j){
        scanf("%d",&a[i][j]);
        c[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];
    }
} int x,xx,y,yy,d; scanf("%d%d%d%d%d",&x,&y,&xx,&yy,&d);
c[x][y]+=d,c[x][yy+1]-=d,c[xx+1][y]-=d,c[xx+1][yy+1]+=d;
for(register int i=1;i<=n;++i){
    for(register int j=1;j<=m;++j){
        a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+c[i][j];
    }
} // 做二维前缀和还原矩阵。

只要注意差分和前缀和的紧密关系，现推都是可以的。

---

最后更新: September 6, 2023