二分
泛化ψ(`∇´)ψ
作用是在单调的序列或者单调的函数当中进行查找。
也可以将最优化问题转化为可行性问题之后进行判定求解。
应用ψ(`∇´)ψ
整数域二分ψ(`∇´)ψ
问题:在单调递增的序列当中查找大于等于 \(x\) 的最小的一个数
开始令两个指针 \(l = 1, r = n\),表示我们当前能确定的答案所在的区间。
我们称 \([1, l)\) 为不可行区间,\([r, n]\) 为可行区间(闭开的原因之后会说),可行区间指的是满足问题约束的区间。
每次取 \(mid = \lfloor (l + r) / 2 \rfloor\)。
如果 \(a_{mid} \ge x\),那么证明 \([mid, n]\) 就一定是可行区间,因为序列单调递增,证明 \(mid\) 之后的 \(a\) 都必然 \(\ge x\)。
所以,我们可以缩小答案区间,令 \(r = mid\)。
反之,证明 \([1, mid]\) 都是不可行的,所以答案区间的左端点肯定不是 \(mid\),所以令 \(l = mid + 1\)。
当 \(l = r\),即答案区间缩小为一个点的时候,此时的 \(a_l\) 就是答案。
如果需要判断无解,开始时令 \(r = n + 1\) ,如果最后 \(l = r = n + 1\) ,那么无解。
这种写法下 \(mid\) 永远不会取到 \(r\),因为如果 \(mid\) 要取到 \(r\),就必须让 \(l\) 不断收缩过来,而当 \(l = r\) 时,循环已经结束了,所以 \(mid\) 不可能取到 \(r\)。
原本的二分区间是 \([1, n]\),现在将其扩大一格变为 \([1, n + 1]\),那么这个越界的下标本身的意义就是“无解”,类似 stl 容器的 end()。
1 2 3 4 5 6 7 | |
如果问小于等于,也就是可行区间在 \(mid\) 左侧,反过来即可:
只不过为了让越界值为 \(0\),需要让 \(mid = \lfloor (l + r + 1) / 2 \rfloor\)。
理解方式同上。
1 2 3 4 5 6 7 | |
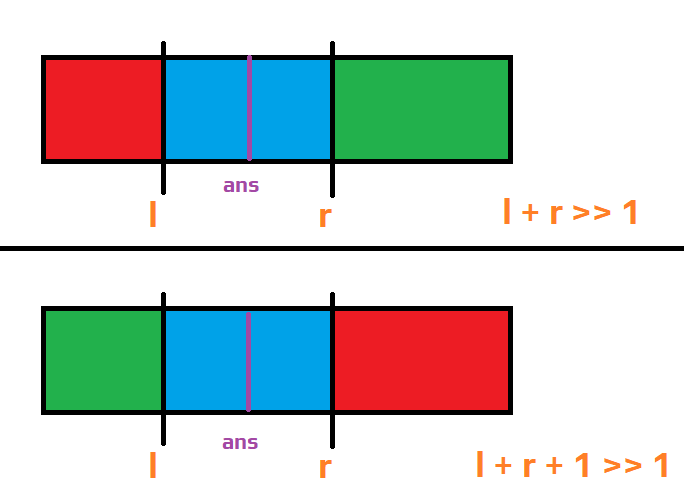
一张图理解,下图绿色为可行区间:
upd on 01.23.23:昨天在 uoj 群里回答了一位小朋友的问题。
也算是有些新的想法吧,就是其实二分的写法有很多种,区别一般在于对答案区间的收缩上。
有的写法是不管 mid 是否 valid 都要取 mid,有的写法是左闭右开,有的写法是左开右闭。
然后循环停止的限制也不一样,所以导致记录答案的方式不一样,这个要自己去区分,不能瞎写(
虽然我用的写法区分了两种方式,但是相对来说不那么容易理解出错?
怪不得 Programming Pearl 说只有 \(20\%\) 的程序员能写对二分((因为很多程序员都是缺乏思考的吧!
实数域二分ψ(`∇´)ψ
和整数域比较类似,不过还需要设置 \(eps\) 来避免精度误差。
因为是实数域上的二分了,用之前那种 +-1 的方式精度是完全不够的(
所以就不管是否合法都收缩到 mid,所以要记录答案而不是可以直接用下标输出。
1 2 3 4 5 6 | |
也可以计算之后设置次数二分。
二分答案ψ(`∇´)ψ
如果一个最优解问题的最优解是 \(x\) ,并且 \(x\) 的一边不合法,一边合法,则这个问题具有单调性。
可以在每次二分的时候将问题转化为是否存在一个方案,使得解为 \(mid\) 。
二分答案 \(x\) 并进行判定。
然后根据可行区间的方式选择二分方式即可。
此类问题的显著特点就是“最小值最大”,“最大值最小”。
不过也有例外,比如 AGC006D。
STL 二分ψ(`∇´)ψ
lower_bound:在有序序列查找大于等于 \(x\) 的第一个。upper_bound:大于 \(x\)。
如果类似 set ,自己带有 lower_bound。
就一定选择容器自身的:s.lower_bound(x) 而不是 lower_bound(s.begin(),s.end(),x)。
这样效率更高,因为 \(s\) 本身不是类似数组那样的随机访问(他没有支持随机访问的迭代器),他是一个树形结构,所以要用 STL 在树上给你实现的 lower_bound。