跳转至

强连通分量

一些定义ψ(｀∇´)ψ

联通分量：对于一个有向图的分量当中的任意两点 \((u,v)\) ，\(\exists \delta (u,v) \land \delta (v,u)\)，则称这个分量为联通分量

强联通分量 SCC：有向图的一个极大连通分量被称作强连通分量，极大的理解就是，不管再加上哪一个边和哪一个节点，他都不再是一个连通分量，也就是“大的不能再大”。

流图：对于一个有向图 \(G=(V,E)\)，\(\exists r \in V\)，满足 \(r\) 可以到达 \(V\) 中的任意节点，则称 \(G\) 为一个流图。

\(r\) 称作流图的源点。

搜索树：对于一个流图 \(G\) 进行深度优先遍历得到的一棵生成树 \(T\) 。

时间戳 \(dfn\) ：对于 \(G\) 中的每一个节点，它在 \(T\) 中被搜索到的顺序（时间）。

为了方便叙述，这里再定义四种边，流图 \(G\) 的所有边必然是这四种边之一

  1. 树边：在搜索树里的边，从 \(u \to v\) ，且 \(u\) 是 \(v\) 的父亲。
  2. 前向边：从 \(u \to v\) ，且 \(u\) 是 \(v\) 在 \(T\) 上的祖先。
  3. 后向边：从 \(u \to v\) ，且 \(v\) 是 \(u\) 在 \(T\) 上的祖先
  4. 横叉边：除了 123 的所有边，必然满足 \(u \to v,dfn_v<dfn_u\)。

Tarjan 算法ψ(｀∇´)ψ

考虑搜索树上的节点如何才能成为 SCC 当中的节点。

首先，一个孤立的点（这里指走出去了就没法回来）必然是一个 SCC。

如果想要更多点加入这个 SCC，实际上就是要找到一个环。

那么后向边必然是有用的，假设 \(v\) 是 \(u\) 的祖先，那么必然存在一个路径从 \(v \to u\)。

而这里又存在一条后向边 \(u \to v\) ，那么必然会出现一个环，也就出现了一个联通分量。

而横叉边也许会有用，只要从 \(u\) 经过一个横叉边走到 \(v\) ，且 \(v\) 可以到达 \(u\) 的祖先节点，那么也会出现一个环，也就是一个联通分量。

那么我们要做的就是在流图上找到尽可能大的，由 \(T\) 经过添加几条后向边和横叉边构成的环。

所以引入一个新的值 \(low_u\) ，表示 \(u\) 和它子树当中的节点能往上（在 \(T\) 当中的上）走到的最高（在 \(T\) 当中深度更低）的节点的时间戳 \(dfn\) 。

如果出现 \(low_u=dfn_u\)，也就是 \(u\) 不可能再往上走，它的 \(low\) 就是自己的 \(dfn\) 的时候，那么 \(u\) 必然是它所在的强连通分量在 \(T\) 上最高的点。

然后在深度优先遍历的时候同时维护一个栈，保存当前能与从这个节点出发的后向边和横叉边构成环的所有节点。

记 \(anc(u)\) 表示 \(u\) 在 \(T\) 上的所有祖先节点，那么栈中保存的实际上就是这两类节点：

  1. \(v \in anc(u)\)，且有可能存在后向边 \(u \to v\)。
  2. \(v \in V\) ，且存在路径 \(\delta(v\to w),w\in anc_u\)。

在满足 \(low_u=dfn_u\) 的时候，把栈的节点不断弹出，直到 \(u\) 出栈，此时当前被弹出的所有节点就构成一个 SCC。

很明显 \(anc(u)\) 中的所有节点都先于 \(u\) 入栈。

所以在 \(u\) 弹出前弹出的一定是第二类节点。

具体实现：

每次新访问一个节点的时候初始化 \(dfn=time + 1,low=dfn\)。

然后访问它的所有出边 \((u,v)\)，如果出边对应的节点 \(v\) 没有访问过（当前访问的是树边），那么就递归然后用 \(low_v\) 更新 \(low_u\)。

反之，如果 \(v\) 已经在栈中了，那么也就是说，存在一条后向边或者横叉边从 \(u\) 出发能到更上面。

根据栈中节点的性质，用 \(dfn_v\) 更新 \(low_u\) 即可。

注意这里要是 \(dfn_v\) 而不是 \(low_v\)，Tarjan 老爷子亲自说过。

（TODO：自己尝试证明一下这儿是为啥）

如果把每一个强连通分量看作一个点。

那么缩完点之后的图就是一个 DAG。

并且 SCC 编号的顺序就是 逆拓扑序。

缩点之后，我们就能非常方便地进行 DP，因为正常 DP 的顺序本来就是拓扑序。

一般都是直接递推求解。

Code 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
std::stack<int>s;
bool ins[si_n]; // in the stack or not
int c[si_n]; //c[x] = the num of SCC which is x iside
std::vector<int>scc[si_n]; // scc[i] -> all node in i-th scc (information of i-th scc)
// 如果没有必要的话可以不要 vector
int dfn[si_n],low[si_n];
int n,m,cnt_t=0,tot=0; // tot = how many scc in the graph. 

void tarjan(int u){
    dfn[u]=low[u]=++cnt_t;
    s.push(u),ins[u]=true;
    for(register int i=e[u].head;i;i=e[i].Next){
        int v=e[i].ver;
        if(!dfn[v]){
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        // 没有访问过，递归搜索然后更新 low。
        else if(ins[v]) low[u]=min(low[u],dfn[v]);
        // 已经在栈中了，用 dfn[v] 来更新 low[u]。
    }
    if(dfn[u]==low[u]){
        ++tot;
        int x;
        do{
            x=s.top(),s.pop(),ins[x]=false;
            c[x]=tot,scc[tot].pb(x);
        }while(u!=x);
    } // 出现了一个 SCC。
}

Edge edag[si_m];
int cnt_d=0;
void add_n(int u,int v){
    edag[++cnt_d].ver=v,edag[cnt_d].Next=edag[u].head;
    edag[u].head=cnt_d;
}
void contract(){
    for(register int u=1;u<=n;++u){
        for(register int i=e[u].head;i;i=e[i].Next){
            int v=e[i].ver;
            if(c[u]==c[v]) continue;
            add_n(c[u],c[v]);
        }
    } // 缩点。
}

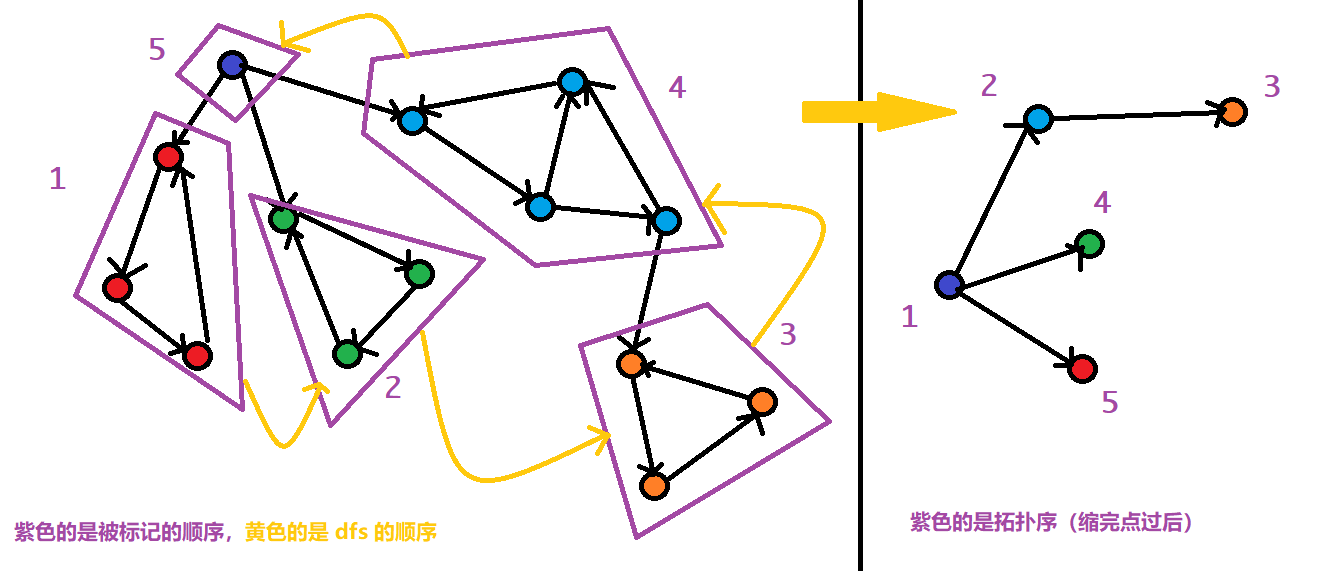
Tarjan 缩完点之后给 SCC 标记的顺序是逆拓扑序的原因非常简单；

因为 Tarjan 的访问顺序是深度优先遍历的顺序（因为使用了栈）。

那么从层的角度来说，更靠上的 SCC 被标记到的时间必然更晚，而 Tarjan 缩完点之后 SCC 构成的图必然是一个 DAG，那么 SCC 的标记顺序就一定是一个合法的逆拓扑序。（可以看这个图理解一下）：

scc-1.png

最后更新: May 9, 2023