Wqs 二分
之前刚学二分的时候做过一道叫 Tree I 的题目,感觉很有意思,不过当时也没怎么深究。
昨天在 uoj 群回答问题的时候得到了清芷姐姐的教导,知道了这玩意儿就是 wqs 二分,因为之前就对这个精妙的套路很感兴趣了,于是决定学习一下。
泛化ψ(`∇´)ψ
假定你有一个限制参数 \(k\),你要求 \(ans(k)\),但是 \(ans(k)\) 求起来是 hard 的。
但是可以快速的对于每一个 \(x\) 求出 \(\max/\min\{ans(i)-ix\}\),且 \(ans\) 是凸的,那么二分这个 \(x\) 就可以了,因为如果 \(ans\) 是凸的,能取到的最优的 \(i\) 就是关于 \(x\) 单调的,这个就可以二分了。
这是 _rqy 姐姐说的,好像对我这种笨蛋来说不是很直观。
所以还是看个例题会比较好。
例题ψ(`∇´)ψ
source: Tree I,by WJMZBMR
给定 \(m\) 条边,\(n\) 个点,每条边可能是可爱边或者不可爱边。
求恰好有 \(e\) 条可爱边的最小生成树。
首先一个比较暴力的做法就是设 \(dp(i, j)\) 表示考虑前 \(i\) 选 \(j\) 个可爱边的 mst。
但是这样复杂度显然上天了吧!!
于是类似之前某个 ds 优化 dp 的题,我们设 \(f(i)\) 表示选了 \(i\) 条可爱边的 mst,要求的答案就是 \(f(e)\)。
注意到我们不能直接给定下标求出 \(f\),这个是困难的。
但是可以发现 \(f\) 是一个下凸的函数(证明先咕咕咕一下)。
也就是长成这样:
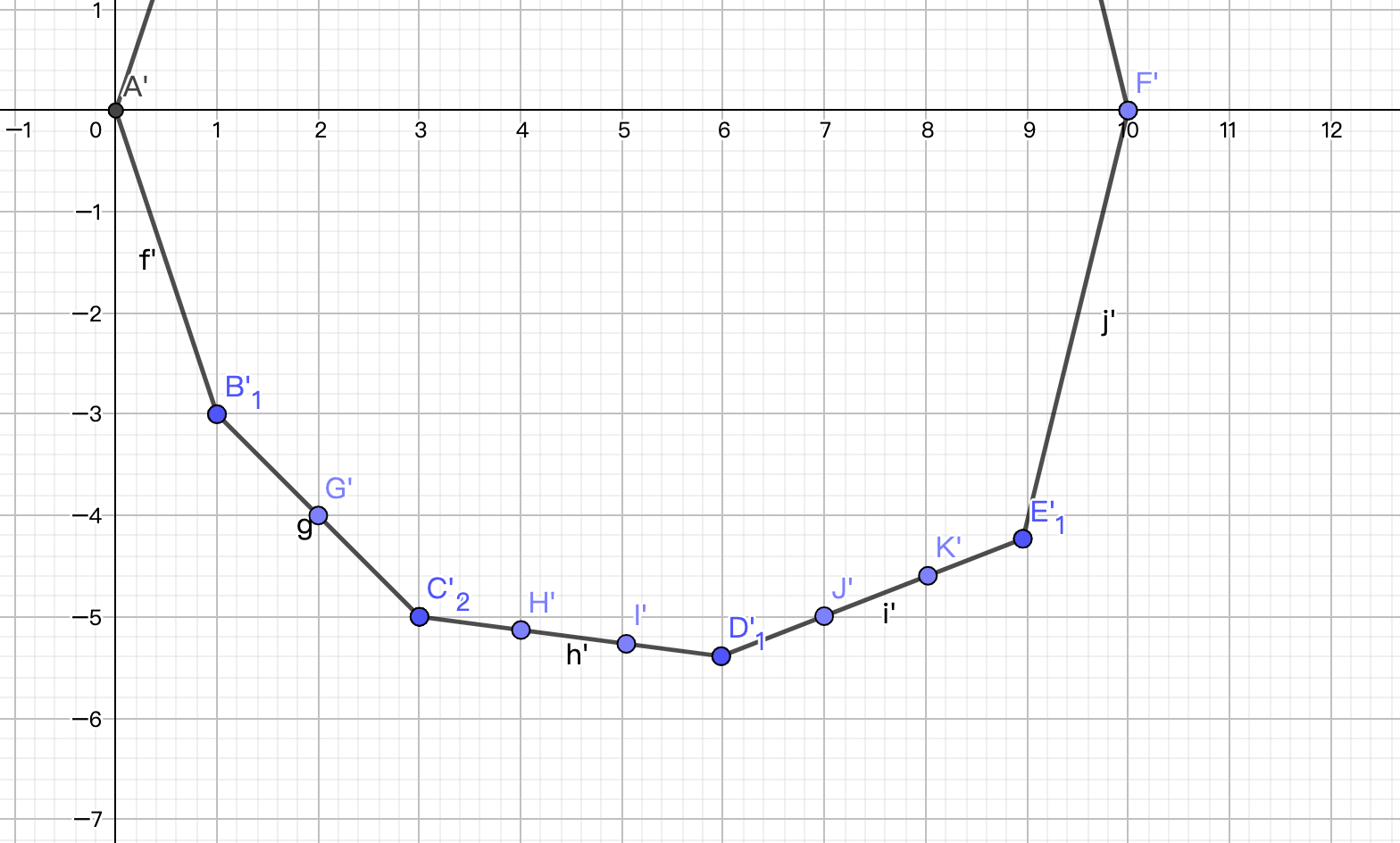
图源 https://www.cnblogs.com/TianMeng-hyl/p/14972355.html。
请读者把它们都当成整点,这里是感性的,本题 \(f(i)\) 显然是 > 0 的。
于是有一种想法是,拉一条直线来切这个凸包,然后显然每个斜率会对应一个切点或者多个切点,我们先不考虑多个切点,也就是假设每一个 \((i, f(i))\) 的两边斜率都不等。
我们是不知道 \(f\) 具体长什么样的,我们只知道他是一个凸包的形式,我们要想办法求出来。
注意到对于下凸函数,当 \(i\) 增加的时候,切线斜率 \(k\) 是单调递增的,并且此时一个 \(k\) 一定对应一个切点。
所以我们有一个想法是,能不能对于一个 \(k\) 求出它对应的切点呢?
这样因为 \(k\) 随着 \(x\) 单调,所以我们就可以通过二分求出 \(e\) 对应的 \(k\) 进而求出 \(f(e)\) 了!
然后其实整个问题的最难点是如何在有限制的情况下求出 mst。
于是有了一个很牛逼的想法。
注意到 \(f(x) = kx + b\),其中 \(b\) 为切线的截距。
因为 \(b = f(x) - kx\),由几何/代数意义,我们可以知道这个 \(b\) 和 \(k\) 是对应的!
然后最神奇的来了,注意到 \(b\) 本质上是给每个可爱边减去一个 \(k\),然后再求有限制的 mst,因为刚才说了,\(b\) 和 \(k\) 是对应的,所以其实就算没有限制,减完之后我们直接求 mst 求出来也一定满足这个选 \(x\) 条的限制!
所以说,我们只需要简单求出 \(b\),加上 \(kx\) 之后就能对于一个 \(k\) 求出 \(f(x)\) 了!
所以我们就只需要二分 \(k\),然后求 \(b\) 进而求 \(f(x)\),反代回去求出 \(x\),然后刚才说了 \(k\) 随着 \(x\) 单调,反过来也是一样的。
所以每次求完之后比较一下 \(x\) 和 \(e\) 进而调整 \(k\) 即可。
But,这只是最简单的情况
注意到其实斜率和切点并不一定能建立函数关系,因为一个斜率可以对应多个切点,比如刚才的情况,有可能出现一个点两边的斜率相等的情况。
那么现在要做的就是解决这个一对多的问题。
一种常见的解决策略是,我们把这多个点融合成一个点考虑。
具体做法是求 mst 的时候如果有相同 weight,让可爱边更靠前。
现在我们直接对着这种情况莽,当一个斜率对应多个切点的时候,我们求出来的 \(x\) 应该是所有满足条件的 \(x\) 里面最大的一个,因为排序的时候已经贪心地让可爱边选的尽可能多。
于是同一条线上的所有点的影响都被考虑到这条线上最靠后的一个切点上了!
也就是说,我们可以只考虑“拐点”即两边斜率不等的点了。
那么就可以直接做,二分满足 \(x > e\) 的所有 \(k\) 里最小的那一个。
很显然 \(e\) 对应的切点一定在这条线上,这个可以反证,然后算 \(f(e)\) 就比较简单了。
假设我们求出来的点的横坐标为 \(x\),显然 \(b = f(x) - kx = f(e) - ke\)
所以 \(f(e) = f(x) - kx + ke\),也就是说只需要求出来 \(x\) 处的截距然后加上 \(ke\) 即可。
Code
1 | |
这个只是最基础的应用,其它的以后有时间就补上。
ref:
另外写这个的时候我删改了很多次。
其实就是想把这个东西是怎么来的说清楚,说的别人能听懂,也问不倒我。
然后就花了不少时间,终于搞懂了。
但是说的时候就有点那啥,写了 4k 全部都注释掉了。
所以这里要特别感谢 \(2 \times \text{mid}(\texttt{'sxp'+'uzr'})\) 小天使。
是他让我突然思路如泉涌,写出了这篇 post!wwwww