CWOI 计数专题(23Sep)
1 2 3 4 5 6 7 8 9 | |
这是 CWOI 的计数专题,题面 pdf 密码和 CWOI 模拟赛一致。
很早之前就想练一练计数了,不过一直没有上这个专题,现在就来做一做。
每个题目分为做的时候的思路,题解,以及总结。
Problem Bψ(`∇´)ψ
Problem Cψ(`∇´)ψ
Thoughts
首先考虑 OEIS /cf
然后并没找到类似的东西,还是老老实实做好了。
观察限制,这个限制说明了每个位置可以填的数是一个确定的集合。
先尝试写出来。
- \(1: \{1, 2, 3\}\)
- \(2: \{1, 2, 3, 4\}\)
- \(3: \{1, 2, 3, 4, 5\}\)
- \(4: \{2, 3, 4, 5, 6\}\)
- ...
- \(n - 2: \{n - 4, n - 3, n - 2, n - 1, n\}\)
- \(n - 1: \{n - 3, n - 2, n - 1, n\}\)
- \(n: \{n - 2, n - 1, n\}\)
换句话说除了开头和结尾的这个四个数,其它的数都有五种选择。
考虑一下选了一个数会有什么贡献。
好像是难以计算的,选了一个会影响至多四个位置,然后这四个位置又可以扩展出影响,咋做。
Solution
Conclusion
Problem Gψ(`∇´)ψ
非常非常有意思的计数题!!!
感觉应该是专题里除了 I 题最难的一道了
数门。
Thoughts
按照这个数据范围,大概是 \(O(d)\) 的,我猜可能是需要枚举一个 \(i + j = d\)。
然后深度为 \(i, j\) 的点分别是一个组合数,然后做一个范德蒙德卷积,之后就可以化成 \(O(d)\) 枚举了。
但是这个,每个点的深度应该怎么确定????不太懂啊,有点 hard 4 me。
而且光枚举这个,LCA 的深度也不知道,那感觉要枚举 LCA,复杂度就变成 \(O(nd)\) 了,哈哈,g 了。
但是这个树比较有前几天 zjk 模拟赛(0905)的那个题的样子,就是形如树状数组展开的样子,不知道有没有什么用。
Solution
通过画图,我们不难发现一个事情,这个树变化的过程,其实可以看做 \(T_i = T_{i - 1} + T_{i - 1}\)。
就比如这样:
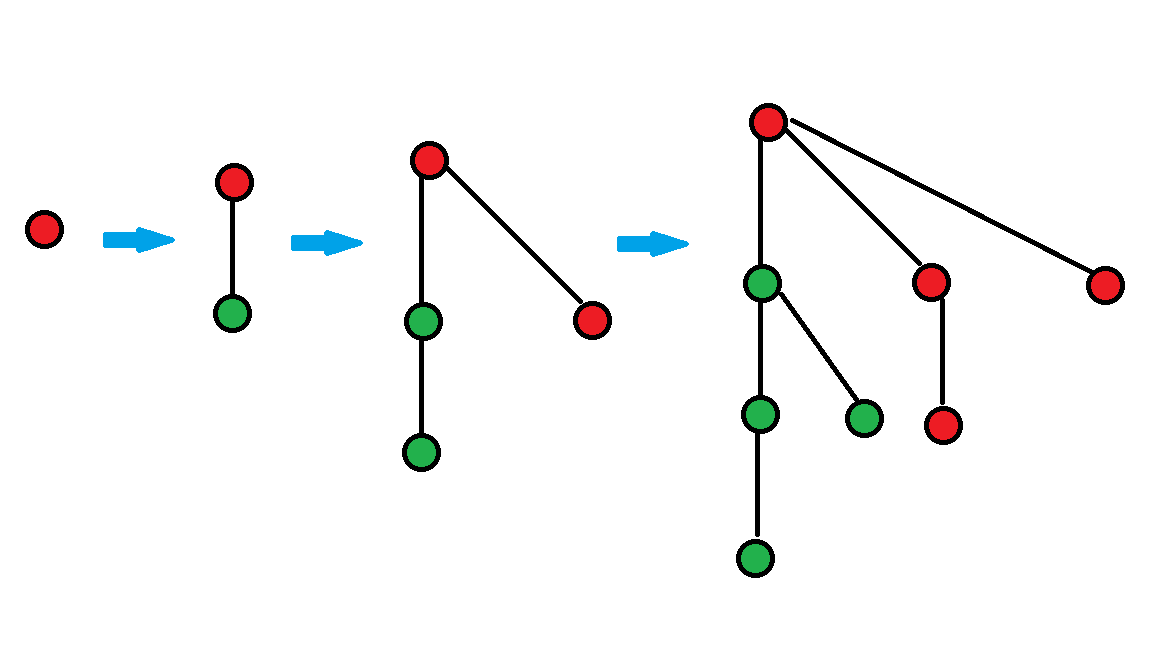
可以发现其实这是一个类似于生长的过程。
于是我们换一个角度考虑,考虑一下这棵树的生成过程。
就是,我们不把加点操作看作“加点”,而是看作“点的移动”
相当于是一开始 \(2^n\) 个点都在编号为 \(0\) 的节点,然后每个点每次扩展可以选择留在这个点,或者是新开一条路。
一共是 \(n\) 次操作,我们可以用二进制状态压缩来唯一描述每一个点。
这也算是说明,题目中告诉我们,树上一共 \(2^n\) 个节点的信息实际上也是一种提示。
于是我们发现,描述每个节点的二进制序列如果转成一个数,把它当作这个节点的编号,如果我们钦定 \(0\) 为根,那么父亲和儿子之间一定满足,\(fa = x - \text{lowbit}(x)\) 的关系。
这就是 zjk 模拟赛的 T2 的样子了,套用那题的思路我们不难想到,这个关系可以用于计算树上距离。
换句话说,两个节点的 LCA 的编号就是两个节点编号对应二进制数从高到低数的 LCP。
那么距离同样也是可以计算的,于是我们只需要对这个进行计数就好了。
仍旧是套用 zjk 模拟赛 T2 的想法,我们枚举 LCP,然后进行计数。
具体来说我们考虑计算距离为 \(d\) 的所有点对 \((x, y)\) 中,\(|\text{LCP}(x, y)| = i\) 的部分。
那么考虑对前一段和后一段分别做组合,前一段因为是 LCA 所以不用管,直接乘上一个 \(2^i\) 即可。
后面的部分要求 \(x, y\) 的这两个后缀中 \(1\) 的个数为 \(d\),这个方案数就是一个组合数 \(\dbinom{2(n - i)}{d}\)。
于是答案变成 \(\sum\limits_{i = 1}^n 2^{i}\dbinom{2(n - i)}{d}\)。
注意到这个柿子是 \(O(n)\) 的,我们直接枚举就是 \(10^9\) 的基本操作量,2s 是肯定过不去的。
但是注意到 \(d\) 的级别在 \(10^7\),于是我们考虑能否把这个柿子转化为 \(O(d)\) 的。
考虑其实我们求的答案就是杨辉三角中的某一列的答案:
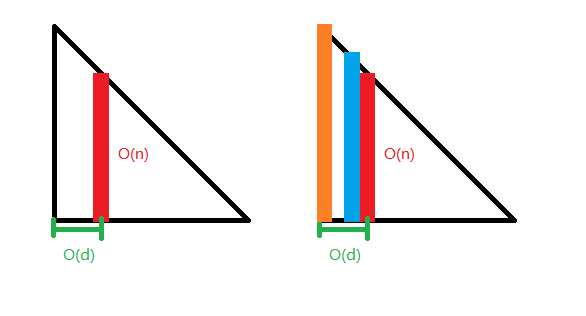
我们想起来,组合数是有一个递推式的,所以我们可以通过这个递推式,尝试找到这一列的组合数和之前的组合数的关系,写出一个关于 \(d\) 的递推式,换句话说令 \(f(x)\) 表示 \(d = x\) 的时候的答案,我们希望知道 \(f(d)\) 和 \(f(d - 1)\) 或者更靠前的状态的关系。
可以发现这里的 \(d\) 被放在了组合数的下部分,那么我们要做的事情就是把组合数的上部分弄成一致的形式,下部分全部是与 \(d\) 相关的一个一次多项式,并且最高次的次数为 \(1\)。
那么就考虑拆组合数:
\(f(d) = \sum\limits_{i = 1}^n2^i\left(\dbinom{2(n - i - 1)}{d} + 2\dbinom{2(n - i - 1)}{d - 1} + \dbinom{2(n - i - 1)}{d - 2}\right)\)
于是我们把三个组合数拆开,分别尝试写成 \(f(d), f(d - 1), f(d - 2)\) 的形式,解一个方程,然后就能得到关于 \(f\) 的递推式了!!!!!
\(f(d) = 2f(d - 1) + f(d - 2) - \dbinom{2(n + 1)}{d}-2\dbinom{2(n + 1)}{d-1}-\dbinom{2(n + 1)}{d-2}\)。
然后就做完了!!!!!!!!
\(f(1), f(2)\) 按着定义算一下就好了!当然 \(f(2)\) 也可以直接写个暴力打表找规律(OEIS)
upd:被 GF 大师 Alpha 怒斥了/ll,好像能更简单,但我不会。
Code
1 | |