CF713C

Description

给你一个序列 \(a\)，长度为 \(n\)。

每次操作可以把 \(a\) 中任意一个元素加一或者减一，代价为 \(1\)。

求使得原序列严格单调递增的最小代价。

\(1\le n \le 3\times10^3, 1\le a_i \le 10^9\)。

Analysis

本题和 POJ3666 十分类似，唯一的区别是，本题要求的是严格单调递增，而 POJ3666 则要求非严格单调递增。

所以可以考虑一个经典 Trick，对于每一个 \(a_i\)，让它减去 \(i\)，本题的严格单调递增就转化为了非严格单调递增。

经过分析之后可以得到一个引理（转化为非严格之后）：

Lemma

设最后得到的序列为 \(b\)，\(S_a,S_b\) 分别为 \(a,b\) 当中出现的所有数组成的集合。

必然存在一组最优解，使得 \(S_b \subset S_a\)。

Proof

首先可以把问题转化为：给定一个序列 \(a\)，构造一个非严格单调递增的序列 \(b\)，使得 \(\sum\limits_{i=1}^{n} |a_i -b_i|\) 最小。

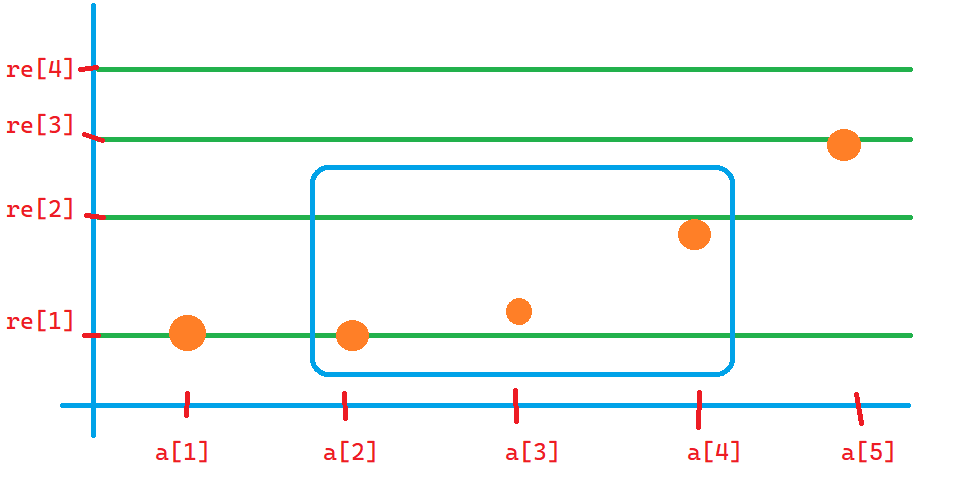
考虑这样的一张图，其中 \(re\) 表示对 \(a\) 排序之后得到的序列，橙色点表示 \(b\)。

对于每个 \(re_i,re_{i+1}\)，把所有在 \([re_i,re_{i+1}]\) 这个区间的 \(b\) 都找出来（上图被框起来的部分）。

统计 \(b_i\) 对应的 \(a_i\) 大于等于 \(re_{i+1}\) 的个数 \(y\)，小于等于 \(re_i\) 的个数 \(x\)。

如果 \(x > y\) ，那么把被框起来的这部分整体向下平移 \(d\) 个单位，使得它们当中的最低点等于 \(re_i\)，总代价就会增加 \(d(y-x)\)，因为 \(x >y\)，所以实际上总代价会减小，就会更优。

\(x < y\) 的时候同理，\(x=y\) 的时候任意选一个方式平移即可。

归纳之后可以发现，任何一个 \(b_i\) ，只要它不属于 \(S_a\)，总是可以把它变成 \(S_a\) 当中的某一个数，且最终答案不会更劣。

引理得证。

Method

根据引理以及其证明过程，不难想到一个 DP 状态：

设 \(dp_{i,j}\) 表示，考虑使 \(a_1 \sim a_i\) 全部满足条件，且使 \(a_i\) 变为 \(re_j\) 时的状态集合。

\(dp_{i,j}\) 的属性是：“总代价的最小值”。

最终答案是所有 \(dp_{n,i}\) 的最小值，其中 \(i \in [1, n]\)。

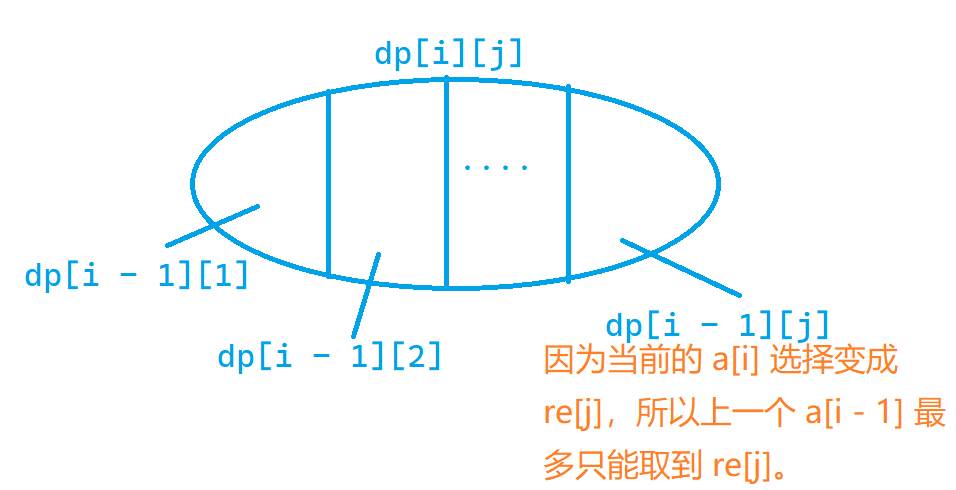
考虑从“上一次决策”进行转移（即是枚举上一次决策选了什么），可以将状态集合划分如下：

那么可以得到一个方程：

\[dp_{i,j} = \min\limits_{0\le k \le j}\{dp_{i-1,k}\} + |a_i - re_j|\]

写出代码：

memset(dp, 0x3f,sizeof dp), dp[0][0] = 0;
for(int i = 1; i <= n; ++i) {
    for(int j = 1; j <= n; ++j) {
        for(int k = 0; k <= j; ++k) {
            dp[i][j] = min(dp[i][j], dp[i - 1][k]);
            dp[i][j] += abs(a[i] - re[j]);
        }
        // 因为初始化只初始化了 dp[0][0]，所以 k 要从 0 开始。
        // 否则从 dp[1][1] 开始的 dp 值就不会被更新，会得到错误的答案。
    }
}

复杂度是 \(\text{O}(n^3)\) 的，需要优化。

瓶颈在于每次枚举 \(k\) 求出 \(dp_{i - 1,k}\) 的“候选集合”中的最小值。

发现当外层循环的 \(i\) 固定，\(j\) 每次增大 \(1\) 的时候，\(dp_{i-1,k}\) 的候选集合只会新加入一个值： \(dp_{i-1,j}\)。

所以可以考虑使用一个变量记录当前候选集合当中的最小值，每次直接使用这个变量进行转移。

那么每次转移的复杂度就从 \(\text{O}(n)\) 优化到了 \(\text{O}(1)\)，总时间复杂度变为 \(\text{O}(n^2)\)，可以通过本题。

Code

int main() { 
    cin >> n;
    for(int i = 1; i <= n; ++i) {
        cin >> a[i];
        a[i] -= i, re[i] = a[i];
    }
    sort(re + 1, re + 1 + n);

    // 初始化写法和 n^3 做法略有不同，但本质一样。
    for(int i = 1; i <= n; ++i) {
        dp[1][i] = abs(a[1] - re[i]);
    }
    for(int i = 2; i <= n; ++i) {
        i64 minv = 2e18;
        for(int j = 1; j <= n; ++j) {
            minv = min(minv, dp[i - 1][j]);
            dp[i][j] = minv + abs(a[i] - re[j]);
        }
    }

    i64 res = 2e18;
    for(int i = 1; i <= n; ++i) {
        res = min(res, dp[n][i]);
    }
    cout << res << endl;
    return 0;
}

当然，实际上可以对 \(re\) 进行一次去重，这样复杂度可以降到 \(\text{O}(n \times |S_a|)\)。

---

最后更新: May 9, 2023