ACWing355
Acwing355 异象石
补充结论的两种证明。
\(\text{Question}\)
动态维护树上使得被选中点联通的边集长度之和的最小值,支持选中,取消选中某个节点。
1e5.
\(\text{Lemma}\)
将所有被选中的节点按照时间戳排序成一圈,答案就是相邻两个节点之间的路径长度值和的二分之一。
\(\text{Proof1}\)
分类讨论证法。
首先有一个结论,一个子树当中的所有节点的时间戳( dfs 序)必然是连续的一段,反过来也一样。
考虑最简单的一种情况:被选中的只有三个节点 \(a,b,c\) (已经排好序)
先走一遍 \(\delta(a,b)\) (对应到代码里就是给答案累加 \(\delta(a,b)\) 的长度),此时 \(\delta(a,b)\) 被覆盖了一次,将 \(\delta(a,b)\) 的长度累加到答案当中。
此时走 \(\delta(b,c)\),有两种情况:
- \(\delta(b,c)\) 不经过 \(a\),这时只能有两种情况(其它的可以归化到这两种)
- 图中情况 \(A\),此时 \(\delta(a,\text{LCA}(b,c))\) 被覆盖一次, \(\delta(b,\text{LCA}(b,c))\) 被覆盖两次 (如果 \(\text{LCA}(b,c)=b\) 就只算一次,之后的同理),\(\delta(\text{LCA}(b,c),c)\) 被覆盖一次。
- 图中情况 \(B\),此时 \(\delta(a,\text{LCA}(a,b))\) 被覆盖一次,\(\delta(b,\text{LCA}(a,b))\) 被覆盖两次,\(\delta(\text{LCA}(a,b),c)\) 被覆盖一次。
- \(\delta(b,c)\) 经过 \(a\) ,这时只能有一种情况(其它的仍然可以归化)
- 图中情况 \(C\),此时 \(\delta(a,b)\) 被覆盖两次,\(\delta(a,c)\) 被覆盖一次。
最后走一遍 \(\delta(a,c)\)
对于上面的 1.1 :\(\delta(a,\text{LCA}(b,c))\) 从被覆盖一次到两次,\(\delta(\text{LCA}(b,c),c)\) 从一次到两次,\(\delta(b,\text{LCA}(b,c))\) 仍旧是两次。
对于上面的 1.2 :\(\delta(a,\text{LCA}(a,b))\) 从被覆盖一次到两次,\(\delta(b,\text{LCA}(a,b))\) 仍旧是两次,\(\delta(\text{LCA}(a,b),c)\) 从一次到两次。
对于上面的 2.1 :\(\delta(a,b)\) 仍旧是两次,\(\delta(a,c)\) 从一次到两次。
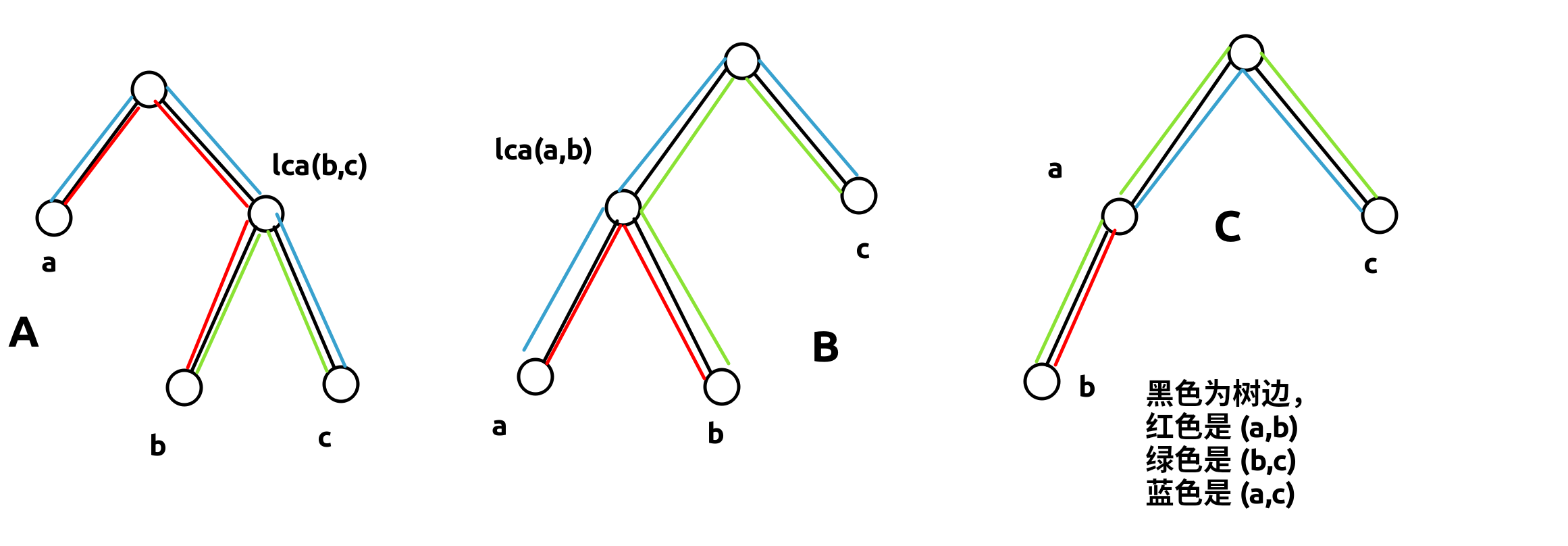
综上所述,在只有三个被选中点的时候,\(\text{Lemma}\) 一定成立。
根据数学归纳法可以得到任意多个被选中点的情况,\(\text{Lemma}\) 得证。
\(\text{Proof2}\)
因为 dfn 连续的一段必然在同一个子树当中。
考虑 \(\text{Lemma}\) 的过程,实际上就是在不断的访问某个子树,处理完这个子树当中会被统计的边,然后退出这个子树。
那就直接看这个深度优先遍历的过程本身,假设你进入到了一个以 \(fa\) 为根的子树,当前走到了一个有异象石的节点 \(u\)。
那么你进入这个子树的时候(也就是处理前面的答案的时候),\(fa \to u\) 实际上已经被算过一次了,当你给 \(u\) 进行统计(也就是要退出子树的时候),\(fa \to u\) 就会被再算一次,并且之后不会回来再次计算。
推广过后得到:一条连接两个有异象石的节点的路径必然会被计算两次。
可以知道 \(\text{Lemma}\) 是正确的。
\(\text{Code}\)
实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82 | #include<set>
#include<cstring>
#include<iostream>
using namespace std;
using i128=__int128;
inline void write(i128 x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+48);
}
constexpr int si=1e5+10;
constexpr int inf=0x3f3f3f3f;
int n,m,tot=0,tim=0;
int head[si];
struct Edge{ int ver,Next,w; }e[si<<1];
inline void add(int u,int v,int w){ e[tot]=(Edge){v,head[u],w},head[u]=tot++; }
int dep[si],f[si][20],dfn[si];
i128 dis[si];
inline void dfs(int u,int fa){
dep[u]=dep[fa]+1,f[u][0]=fa,dfn[u]=++tim;
for(register int i=1;i<=19;++i) f[u][i]=f[f[u][i-1]][i-1];
for(register int i=head[u];~i;i=e[i].Next){
int v=e[i].ver,w=e[i].w;
if(v==fa) continue;
dis[v]=dis[u]+w,dfs(v,u);
} return ;
}
inline int Lca(int u,int v){
if(dep[u]<dep[v]) swap(u,v);
for(register int i=19;i>=0;--i){
if(dep[f[u][i]]>=dep[v]) u=f[u][i];
} if(u==v) return u;
for(register int i=19;i>=0;--i){
if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
} return f[u][0];
}
inline i128 path(int u,int v){ return 1ll*dis[u]+1ll*dis[v]-2ll*(dis[Lca(u,v)]); }
std::set<std::pair<int,int>>s;
i128 ans=0;
inline void Insert(int x){
if(s.size()==2) return (void)s.insert({dfn[x],x});
auto now=s.insert({dfn[x],x}).first;
auto Pre=std::prev(now),Nex=std::next(now);
if(Pre==s.begin()) Pre=--(s.find({inf,inf}));
if(Nex==(--s.end())) Nex=++(s.begin());
std::pair<int,int>u=*Pre,v=*Nex;
ans-=path(u.second,v.second);
ans+=path(u.second,x)+path(x,v.second);
}
inline void Delete(int x){
if(s.size()==3) return (void)s.erase(s.find({dfn[x],x}));
auto now=s.find({dfn[x],x});
auto Pre=std::prev(now),Nex=std::next(now);
if(Pre==s.begin()) Pre=--(s.find({inf,inf}));
if(Nex==(--s.end())) Nex=++(s.begin());
std::pair<int,int>u=*Pre,v=*Nex;
ans+=path(u.second,v.second);
ans-=path(u.second,x)+path(x,v.second);
s.erase(now);
}
int main(){
memset(head,-1,sizeof head);
cin>>n,s.insert({-1,-1}),s.insert({inf,inf}); //左右各塞一个空余节点防止越界
// 这招是打 CF 的时候跟 jiangly 学的
for(register int i=1;i<n;++i){
int u,v,w; cin>>u>>v>>w;
add(u,v,w),add(v,u,w);
} dfs(1,0);
cin>>m;
while(m--){
char op; cin>>op; int x;
if(op=='+') cin>>x,Insert(x);
if(op=='-') cin>>x,Delete(x);
if(op=='?') write(ans/2),putchar('\n');
} return 0;
}
|
最后更新:
May 9, 2023
