ACWing277

Acwing277 饼干

Description

圣诞老人共有 \(M\) 个饼干，准备全部分给 \(N\) 个孩子。

每个孩子有一个贪婪度，第 \(i\) 个孩子的贪婪度为 \(g[i]\)。

如果有 \(a[i]\) 个孩子拿到的饼干数比第 \(i\) 个孩子多，那么第 \(i\) 个孩子会产生 \(g[i] \times a[i]\) 的怨气。

给定 \(N、M\) 和序列 \(g\)，圣诞老人请你帮他安排一种分配方式，使得每个孩子至少分到一块饼干，并且所有孩子的怨气总和最小。

\(1 \le N \le 30\)，\(N \le M \le 5000\)，\(1 \le g_i \le 10^7\)

要求输出方案。

Analysis

发现直接求解的话很不好搞，因为每发出一块饼干的时候，你都要扫一遍进行统计，而且随着饼干的发出，怨气值是有可能减少的。

因为，如果给第 \(i\) 个孩子多分配了一个糖果，在他前后的孩子的怨气值都是会受到影响而改变的，找不到一个可以只影响 \(i\) 前面或者后面的 ”阶段“。

所以考虑一个比较明显的贪心，对 \(g\) 降序排序，则从前往后分配的饼干数量必然单调不上升。

这个证明可以利用贪心算法中的一个经典不等式：排序不等式。

具体证明过程略。

排序过后，因为从前往后分配的饼干数量单调不上升，那么当前面的孩子分配的饼干数不改变的时候，

如果后面的孩子分配的饼干数量增加，对前面的孩子的怨气值是没有影响的。

所以，DP 的”阶段“就浮现出来了，就是 ”前 \(i\) 个孩子“ （排序过后）。

而题目中还有一个要素 \(M\)，所以我们考虑把这两个要素结合起来得到一个 DP 状态：

设 \(dp_{i,j}\) 表示考虑前 \(i\) 个孩子，总共分配了 \(j\) 块饼干的所有方案，属性为怨气总和的 \(\min\)。

如果直接考虑划分子集的话，是非常麻烦，不便于转移的。

设 \(b_i\) 为排序后处在位置 \(i\) 的孩子当前拿到的饼干数量，考虑如下的两种情况：

1. \(b_i = b_{i-1}\) ，那么转移的时候 \(a_i = a_{i-1}\)，需要提前知道 \(a_{i-1}\)。
2. \(b_i = b_{i-1}\) ，那么转移的时候 \(a_i = a_{i-1} +1\)，还是需要提前知道 \(a_{i-1}\)。

但是这个时候是在 DP，你要知道 \(a_{i-1}\)，就必须要知道前面有多少个孩子获得的饼干数量和 \(i-1\) 一样。

这样就需要话额外的时间去枚举可能的情况，如果按照这样推下去，时间复杂度将会爆炸，无法接受。

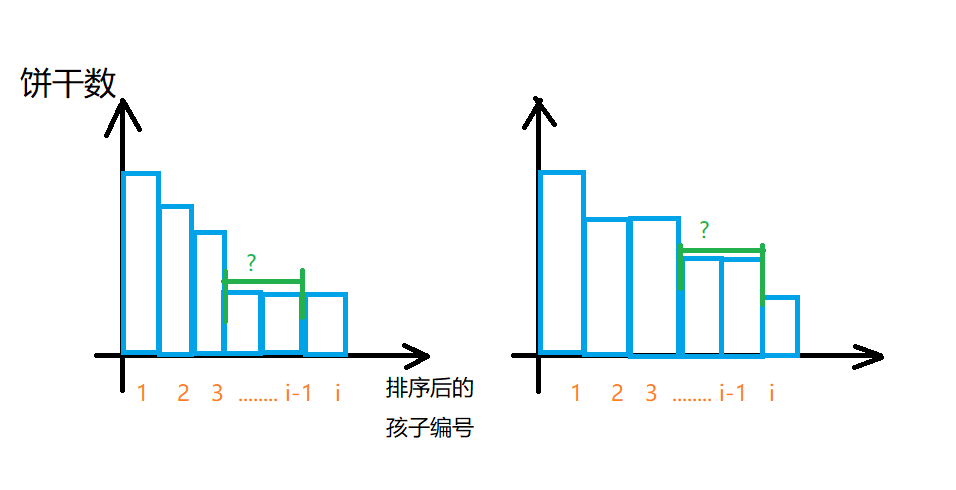
就像下图所示，你不知道 \(?\) 的距离到底有多长，所以需要枚举。

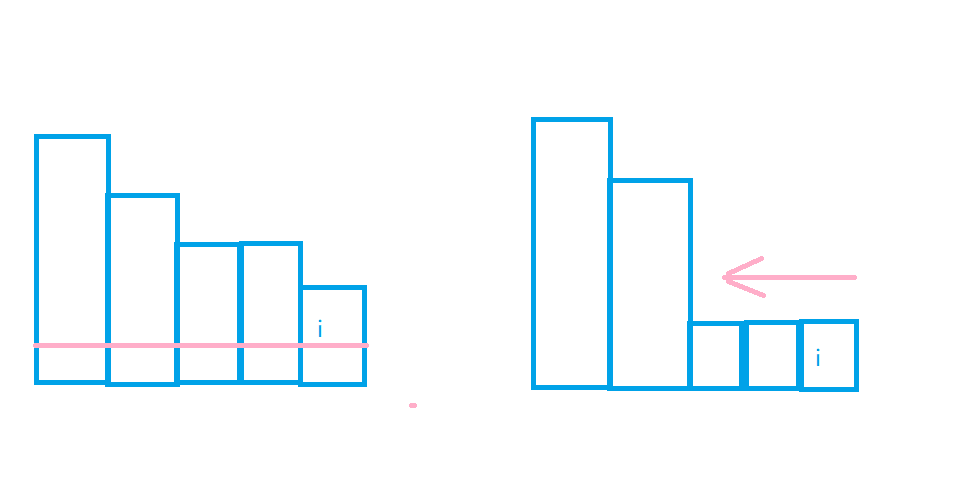
但是观察一下，假设 \(b_i > 1\)，也就是下图所示的左边的情况。

如果我们给前面的 \(b\) 都减去 \(1\)，相对大小是没有变的，怨气值也是没有增加的。

所以可以发现，在这种情况下 \(dp_{i,j} = dp_{i,j - i}\)。

而你枚举更新的时候不可能从一个分配了更多饼干的状态转移到分配了更少的状态。

所以 \(dp_{i,j - 1}\) 一定是 \(dp_{i,j}\) 的子集，就没有后效性了，可以直接转移。

如果是上图右边的情况，\(b_i\) 等于 \(1\)，我们就需要知道前面有多少个孩子和 \(b_i\) 一样也只拿到了 \(1\) 块。

因为每个孩子至少要拿到一块，所以不能再减了。

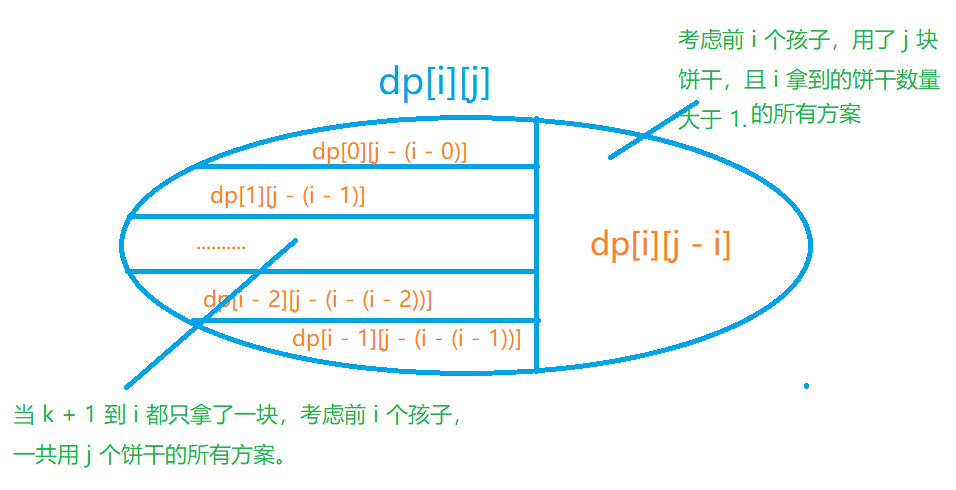
那么就找到一个位置 \(k\)，使得 \(b_k >1,b[k + 1 \sim i] = 1\)。

然后把 \(b[1\sim k]\) 的部分转化成左边的情况，\(b[k+1 \sim i]\) 的部分单独计算。

因为你不知道具体 \(k\) 到底是多少，所以枚举所有情况取最小值即可（这里就是在划分 \(dp_{i,j}\)）。

所以可以得到这种情况的转移方程：

\[dp_{i,j} = \min\limits_{0 \le k < i}\{dp_{k,j-(i-k)}+k\times\sum\limits_{l = k+1}^{i} g_l\}\]

后面的 \(\sum\) 可以直接前缀和做。

得到这样的划分方式（绿字是对应子集的意义，橙字是子集对应的状态）：

所以可以得到状态转移方程：

\[dp_{i,j} = \min\begin{cases}dp_{i,j - i} \\ \min\{dp_{k,j-(i-k)} + k\times \sum\limits_{l = k + 1}^i g_l\}\end{cases}\]

初始化 \(dp_{0,0} = 0\)，其余为 \(+\infty\)，答案为 \(dp_{n,m}\)。

本题还要求输出方案，所以考虑记录一个pair 数组 \(pre_{i,j}\)，表示使 \(dp_{i,j}\) 发生更新的状态的 \(i,j\) 分别是什么。

在 \(dp_{i,j}\) 发生更新的时候记录对应的 \(pre_{i,j}\) 即可。

然后构造方案的时候利用递归构造，设 \(solve(x,y)\) 表示处理 \(dp_{x,y}\) 对答案造成的影响。

那么先递归处理 \(solve(pre_{x,y}.first,pre_{x,y}.second)\)。

递归到边界 \(x = 0\) 就返回。

实际上就是推到最前面（\(dp_{1,blabla}\) 的状态），然后往后根据从哪里转移过来计算答案。

也就是再次模拟一遍转移。

具体实现看代码。

Code

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int si = 30 + 10;
const int sii = 5e3 + 10;

int n, m;
int dp[si][sii];
pair<int, int> g[si];
pair<int, int> pre[si][sii];
int sum[si], ans[si];

void solve(int x, int y) {
    if(!x) return;
    // 到达边界

    auto [px, py] = pre[x][y];
    solve(px, py);
    // 先递归处理 pre[x][y]

    if(px == x) 
        for(int i = 1; i <= x; ++i) 
            ans[g[i].second] += 1;
        // from dp[x][y - x];
        // 此时给 1 ~ x 所有数都加上 1, 因为转移的时候它们都减去了 1。
    else 
        for(int i = px + 1; i <= x; ++i)
            ans[g[i].second] = 1;
        // from dp[px][y - (x - px)];
        // 此时把状态对应的 k + 1 ~ i 的部分设置为 1。
}

int main() {
    cin >> n >> m;
    for(int i = 1; i <= n; ++i) {
        cin >> g[i].first;
        g[i].second = i;
    }
    sort(g + 1, g + 1 + n);
    reverse(g + 1, g + 1 + n);

    sum[0] = 0;
    for(int i = 1; i <= n; ++i) sum[i] = sum[i - 1] + g[i].first;

    memset(ans, 0, sizeof ans);
    memset(dp, 0x3f, sizeof dp);
    dp[0][0] = 0;

    for(int i = 1; i <= n; ++i) {
        for(int j = i; j <= m; ++j) {
            // 注意 j 是从 i 开始枚举的，也就是先保证 1 ~ i 的每个孩子至少都有一块。
            dp[i][j] = dp[i][j - i], pre[i][j] = {i, j - i};

            for(int k = 0; k < i; ++k) {
                int trans = dp[k][j - (i - k)] + k * (sum[i] - sum[k]);
                if(dp[i][j] > trans) {
                    dp[i][j] = trans;
                    pre[i][j] = {k, j - (i - k)};
                }
            }
            // 你初始化只初始化了 dp[0][0]，那么要转移下去必然要利用到它。
            // i = j, k = 0 的时候就会利用到。
            // 所以不要忘记 k 可以等于 0。
        }
    }

    cout << dp[n][m] << endl;

    solve(n, m);

    for(int i = 1; i <= n; ++i) cout << ans[i] << " ";

    return 0;
}

复杂度 \(\text{O}(n^2\times m)\)。

Tag : 线性DP/构造方案/思维/排序不等式

---

最后更新: May 9, 2023