跳转至

CF & AT 题解

某些恶心题就不补了。

ATCoder，NowCoder，Codeforces的比赛实际上都会放到这里面。

然后CF的思维题一类的也会在这儿。

Codeforces #734ψ(｀∇´)ψ

Contest ID:1551

在学校和整个机房一起VP的。

Aψ(｀∇´)ψ

\(1\) 块的硬币用 \(c_1\) 个, \(2\) 块硬币用 \(c_2\)个。

问你凑出 \(n\) 元时的 \(\min(|c_1-c_2|)\)

一眼题。

要 \(|c_1-c_2|\) 最小说白了就是尽量平均。

那么就尽量的用一个 \(1\) 的同时也用一个 \(2\)。

所以把 \(n\) 除以 \(3\)，得到 \(c_1\) 和 \(c_2\) 各自必须要有的个数（此时 \(c_1=c_2\)）。

然后 \(n\) 无非就是剩下 \(0,1,2\) 这三种情况。

如果不剩那么直接输出。

如果余 \(1\) 那么多加一个 \(1\) 元。

如果余 \(2\) 那么多加一个 \(2\) 元。

B1ψ(｀∇´)ψ

给你一个字符串，每个字符可以涂上红或绿，或者不涂。

涂上相同颜色的所有字母相互不能相同，且红色和绿色的个数都为 \(Q\)，求 \(\max\{Q\}\)。

首先考虑第一个条件。

转化一下也就是说每一种字母最多只能有两个被涂上颜色。

所以我们开一个桶统计一下每一个字母的出现次数并对其进行判断。

再考虑第二个条件。

因为只会有两种颜色，所以涂上颜色的点的个数必须是偶数（ \(2\) 的倍数）。

那么思路就出来了，统计一下每一个字母出现的次数，并且统计它最多有多少个字母可以被涂上颜色。

对于每一种字母，如果它的个数小于等于 \(2\) 那么就都可以被涂色，如果大于等于 \(3\) 就只有两个可以被涂上颜色。

因为有两种颜色，所以答案就是可以被涂上颜色的字母个数除以 \(2\)。

如果最后可以被涂上颜色的字母个数是个奇数，就需要先减 \(1\) 再除 \(2\)。

B2ψ(｀∇´)ψ

大体同 B1,现在字符串变成了序列，而且有 \(k\) 种不同颜色。

只要求你输出方案即可。

从B1的角度考虑，现在有 \(k\) 种不同颜色。那么我们仍旧是统计每一个不同的元素出现多少次。

如果大于 \(k\) 那么就只有 \(k\) 个可以被涂色。

反之都可以。

然后统计完之后我们按 \(a[i]\) 的大小排个序。

也就是把同一种都扔到一起处理。

对于每一种，我们只涂前 \(k\) 个（保证不重复而且涂够），就可以了。

但是我们要输出方案，所以需要记录一下元素的位置。

Cψ(｀∇´)ψ

只用五个字母 \(\{a,b,c,d,e\}\) 组成一篇文章，

若果其中一个字符的出现次数比其它的加起来都多那么这篇文章就是好的。

给定几个单词，求最长的好文章的单词数。

看到只有五个字母，我直接高兴了起来。

看到时限4s，我的嘴角就直接扬了起来。

这不明摆着让你打暴力吗？

所以直接统计每个字符的出现次数。

然后对于每种字符我们排序贪心一下，如果说可以选当前单词，即更新答案。

（说是简单暴力+贪心，我却写了半小时，wtcl）

D1 D2 E Fψ(｀∇´)ψ

待补

Codeforces #735ψ(｀∇´)ψ

Contest ID:1554

五题场，我居然有ABCD。

Aψ(｀∇´)ψ

问你一个序列的所有长度不小于 \(2\) 的子区间的最大值和最小值乘积的最大值。

从数据范围就能发现，一定是个 \(\text{O}(T\times n)\) 的算法。

所以想到了单调队列或者单调栈维护。

但是仔细想想，这个子区间的长度只能为 \(2\)。

为何？

我们就先从长度为 \(2\) 的区间开始考虑。

那么很明显权值就是 \(a[l] \times a[r]\) 。

考虑一个长度为 \(3\) 的区间，且里面的元素是 \(\{a,b,c\}\) （按顺序）。

  • 假设 \(b\) 是最大的，那么它就会和 \(\min(a,c)\) 结合，那么就和长度为 \(2\) 的没有任何区别。

  • 假设 \(a\) 是最大的，那么有如下两种情况。

    1. \(b\) 比 \(c\) 小，那么这个区间的权值一定是 \(a \times b\) ，转化成了长度为 \(2\) 的情况。
    2. \(b\) 比 \(c\) 大，那么这个区间的权值就是 \(a \times c\) ，但是很明显， $a\times b $ 也就是长度为 \(2\) 的时候绝对比这个 \(a\times c\) 更优（因为我们最终要求的是最大值）

反过来同理，然后把这个结论扩展到 \(n=4,5,6...\) 就能证明结论正确。

所以现在只需要读入的时候让相邻的元素两两相乘，求乘积的最大值，这个最大值就是答案。

Bψ(｀∇´)ψ

求所有一个序列里所有的 \(i\times j -k\times(a_i \operatorname{or} a_j)\) 的 \(\max \ \ (k \in [1,\min(n,100)])\)

（tips：一个数按位或上另一个数，这个数绝对不会减小）

我是直接凭感觉猜的结论：\(i\in [\max(n-100,1),n),j=i+1\) 然后暴力跑。

这里有个严谨的做法（来自lg题解区）

fARHSg.png

Cψ(｀∇´)ψ

求最小的 \(k\) 满足 \(k\not\in \{n \operatorname{xor}0,n \operatorname{xor}1...n \operatorname{xor}m\}\)

\(n,m\) 是 \(10^9\) 级别。

根据异或的某个性质： \(n \operatorname{xor} k >m \Leftrightarrow n \operatorname{xor} k \ge m +1\)

设 \(x_i=(m+1)_2\) 的第 \(i\) 位。

设 \(k_i=(k)_2\) 的第 \(i\) 位。

那么有四种情况：

  • \(x_i=k_i=1\Rrightarrow k_i=0\)
  • \(x_i=k_i=0\Rrightarrow k_i=0\)
  • \(x_i=1,k_i=0\Rrightarrow k_i=1\)
  • \(x_i=0,k_i=1\Rrightarrow k_i=0\)

稍微用位运算搞一下就行了。

Dψ(｀∇´)ψ

我目前做过最傻逼的构造。

容易发现 aaba+k 形式的构造是对的。

就是前面一段 a 比后面一段多一个，然后在中间插一个 b

如果 n 是奇数在后面补一个非 a\b 的字符就行。

注意特判 \(\text{length}=1\)

Eψ(｀∇´)ψ

待补

Edu #112ψ(｀∇´)ψ

Contest ID:1555

Aψ(｀∇´)ψ

有 \(6\) 片的（ \(15min\) ） ,\(8\) 片的( \(20min\) ), \(10\) 片的( \(25min\) )Pizza。

现在需要至少 \(n\) 片 Pizza，问最小的等待时间。

不难发现每种平均一下，都是\(2.5\) 分钟一片。

然后我们发现，如果你需要的小于等于六片，直接 \(15min\) 就行。

然后考虑大于六怎么做。

发现其实这三个数可以凑出所有大于 \(6\) 的偶数。

反向思维。

如果你做过这道题： P3951 [NOIP2017 提高组] 小凯的疑惑

那么可以拓展成三元的偶数情况，然后就能证出这三个数最大不能凑出的偶数是 \(4\)，那么最大的不能凑出的数就是 \(5\)。

然后就整完了，这题直接特判就行。

Bψ(｀∇´)ψ

给一个宽和高给定的房间，一张已经放好的桌子的对角线顶点坐标。

再给定一张长宽固定的桌子，问原来的桌子至少要移动多少个单位才能放下新桌子（曼哈顿距离）。

新的桌子要最优，就只能放在四个角上，可以四种情况都枚举。

也可以特判贪心一下，比较简单。

Cψ(｀∇´)ψ

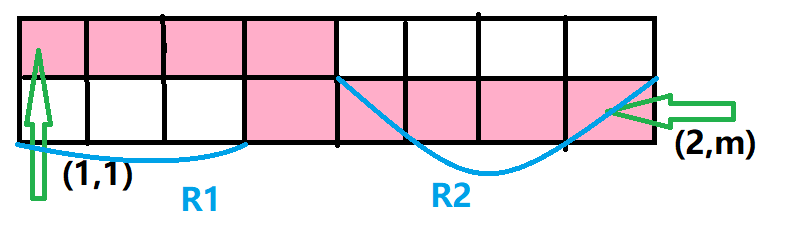
Alice 和 Bob 在一个 \(2 \times m\) 的矩形上玩游戏，矩形的每一个格子上都有一个数 $ a_{i,j} $

Alice 和 Bob 一开始站在左上角格子 \((1,1)\) 上，每个人都只能向下或者向右移动，直到移动到终点 \((2,m)\) 上，经过一个格子时会取走格子上的数，赢得相应的得分

Alice 首先开始移动，Bob 不能取走 Alice 已经取走的数

Alice 期望最小化 Bob 的得分，Bob 则希望最大化自己的得分

求Bob 的最大得分。

读一下题发现，因为只有两行而且只能向右或者向下。

也就是说他们都只能向下一次，这就是一个入手点。

注意到Alice走过之后数字就没了，而且Alice先手，所以Bob一定要尽量避开Alice走过的路。

fEDHiQ.png

比如上图，粉色部分是Alice走过的路，那么Bob能取到数字的只有 \(R1\) 或 \(R2\) 两部分。

也就是他不是从上面先走通再下去就是先下去然后走通。

那么我们枚举Alice下去的这个位置，然后利用前缀和维护一下求个 \(\max\) 即可。

D E Fψ(｀∇´)ψ

待补

Codeforces #736(div1+2ψ(｀∇´)ψ

Contest ID:div1 1548,div2 1549

我依旧div2 ABCD……

其他的目前还不会

div2Aψ(｀∇´)ψ

傻逼送分题。

让你找一对 \((a,b)\) 满足 \(a \operatorname{mod} P = b \operatorname{mod} P\)

\(P\) 是一个大于等于 \(5\) 的质数。

所以 \(P\) 不可能是偶数，也就是说 \(P-1\) 一定是偶数。

那么直接找 \(P-1\) 的随便两个大于等于二的因子。

为了方便直接输出 \(2\) 和 \((p-1)/2\) 即可。

div2Bψ(｀∇´)ψ

考虑一下可以发现对于在第 \(i\) 列的卒要想到达对面一定满足一下两个条件：

  • 第一排的第 \(i\) 列没有敌兵，直接走过去即可。

  • 第一排的第 \(i-1\) 或 \(i+1\) 列有敌兵且之前没有我方兵去吃。

然后稍微模拟一下就行了。

div1Aψ(｀∇´)ψ

甚至比 div2A还SB的zz题。

看起来是什么高大上的图论，然而直接维护每个点的出度就完了。

细节稍微有点卡人，注意一下就行。

div1B （Great）ψ(｀∇´)ψ

啊这道题有点毒瘤，我调了一个小时左右（要不是比赛延时10min我真的做不起）。

给一个序列 \(a[]\) 的区间 \(a_i,a_{i+1},...a_j\)。

这个区间是好的，当且仅当存在一个 \(\ge 2\) 的 \(m\)，使 \(a_i \operatorname{mod} m=a_{i+1} \operatorname{mod} m =...=a_j \operatorname{mod} m\)

问给定序列 \(a[]\) 的最大好区间的大小。

说实话……我是真的不清楚这个神仙思路怎么来的。

对于 \(\forall x \in(i,j]\) ，令 \(a[x]\) 减去 \(a[x-1]\) （之后要取绝对值）

然后你会发现减了之后，假设 \(a[x] \operatorname{mod} m=k\) 。

那么 \(k\) 就会被消掉了！！！

也就是 \(|a[x]-a[x-1]| \operatorname{mod} m =0\) ！！！

那么反过来，我们只需要找到一个最长的 \(\gcd\) 相同（且 \(\gcd>1\)）的区间就行了！！！

然后发现 \(\gcd\) 这玩意儿不太好用线段树维护（常数太大了），分块的 \(\text{O}(n\sqrt{n})\) 很容易本题的某些神仙数据卡死。

然后我们就想到了好玩的 \(\text{ST}\) 表！！！！

所以我们直接利用 \(\text{ST}\) 表来维护区间的 \(\gcd\)。

但是这里要求的是最长的区间长度，再套一个数据结构就会炸。

那么就掏出 \(\text{O}(n\log n)\) 的二分吧。

所以先差分取个绝对值再预处理出 \(\log_2\) 。

然后利用 \(\text{ST}\) 表维护 \(\gcd\)。

之后枚举区间左端点，同时二分区间右端点。

并用维护的信息进行check即可。

应该是我最近做的最有意思的题了。

此处二分写法相较于我平时的写法稍微有点怪，不过也是对的。

这种写法是不会取到 \(l\) 的，方便本题更新答案。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include<bits/stdc++.h>
using namespace std;

const int si=2e5+10;
#define int long long
int st[si][20];
int a[si],logt[si];
int T,n,res=0;

int gcd(int a,int b){
    if(!b) return a;
    return gcd(b,a%b);
}
int check(int l,int r){
    return gcd(st[l][logt[r-l+1]],st[r-(1<<logt[r-l+1])+1][logt[r-l+1]]);
}
void STprework(){
    for(register int i=2;i<=n;++i){
        logt[i]=logt[i>>1]+1;
    }
    for(register int i=1;i<=n;++i){
        int o=abs(a[i]-a[i+1]);
        st[i][0]=o;
    }
    for(register int i=1;i<=logt[n];++i){
        int toj=(n+1)-(1<<i);
        for(register int j=1;j<=toj;++j){
            st[j][i]=gcd(st[j][i-1],st[j+(1<<(i-1))][i-1]);
        }
    }
}

signed main(){
    scanf("%lld",&T);
    while(T--){
        scanf("%lld",&n);
        for(register int i=1;i<=n;++i){
            scanf("%lld",&a[i]);
        }n-=1;
        STprework();
        res=0;
        for(register int i=1;i<=n;++i){
            if(st[i][0]==1) continue;
            int l=i,r=n;
            while(l<r){
                int mid=(l+r+1)>>1;
                if(check(i,mid)==1) r=mid-1;
                else l=mid;
            }
            res=max(res,l-i+1);
        }
        res++;
        printf("%lld\n",res);
    }
    return 0;
}

Codeforces #737(div2)ψ(｀∇´)ψ

Contest ID:1557

对这次比赛的出题人非常无语。

没有水平就别来出题好不好？

您只会拿着板子，套路题改一点点，加加码量，输出方案来恶心人吗？

A的贪心，B的离散，C的组合数，D的线段树优化DP，都是老trick，E出个交互，烂到大部分交的随机算法都能过st。

我没AK，只是想喷一喷出题人，反正这比赛风评挺差的。

不写了，浪费时间，期待 #738 能有质量一点。

Atcoder Beginning Contest 214ψ(｀∇´)ψ

Contest ID:abc_214

因为AT比赛没有那么频繁，所以AT的题解也都扔到Codeforces Solutions 来了。

明明可以写出EF但是E傻逼了。

我不配 8kyu。

A B Cψ(｀∇´)ψ

A是语法题，B是暴力枚举，C是断环成链模拟

D & CF915Fψ(｀∇´)ψ

这是个经典 trick，你会发现这两题竟然和本次D题惊人的相似：

全部都是 \(u,v\) 之间简单路径上的一些信息统计。

特别是 CF915F，你惊奇的发现一个 \(\min,\max\) 做减法后求和，一个直接就是对 \(\max\) 求和。

所以这两道题，完全一致。

此 Trick 的做法就是利用并查集按顺序合并然后计算贡献。

这题就是按边权值从小到大合并连通块然后计算贡献。

首先考虑简单路径上的 \(w_{\max}\)

我们先对于所有代表边的三元组 \((u,v,w)\) 按照 \(w\) 从小到大排序，然后依次扫描每一条边。

然后使用并查集进行维护连通块，每一次扫描都把 \(u,v\) 合并起来。

因为现在所有三元组按 \(w\) 单调不下降，也就是说你对于当前扫描到的 \(w\)，他能做出贡献的路径只有 \(siz[\text{root}(u)]\times siz[\text{root}(v)]\) 这么多个。

为啥，你看后面的没有被加进来的三元组，每一个的 \(w\) 都比你大，那后面的情况你肯定没法做出贡献。

那么，在每一次合并的时候计算贡献 \(w \times siz[\text{root}(u)]\times siz[\text{root}(v)]\) 即可。

然后 CF915F 就完全一样，点化边直接求两遍，一次升序一次降序排序，然后两个总贡献做减法即可。

那一题唯一的新 Trick 就是对于跑 \(\min\) 的 \(\texttt{dsu}\) 的时候，对于 \((u,v)\) 两点之间的边权是 \(\min(val[u],val[v])\)。

\(\max\) 同理即可。

E F G Hψ(｀∇´)ψ

待补

Codeforces #738ψ(｀∇´)ψ

Contest ID:1559

CN round ，体验还可以。

可能是今年的最后一次实地CF了、

Aψ(｀∇´)ψ

稍微推一下可以发现，把整个序列全部 \(\&\) 起来可以最优。

然后随便整一整就可以发现一定能构造出这种方案。

（之后啥时间仔细写下吧）

Bψ(｀∇´)ψ

感觉是个很熟悉的trick？

就是给你一个已经填上两种字符 R,B 的字符串（有些地方空着）。

问你怎么样补全剩下的空余能够使相邻两个字符相等的情况最少。

你只能填 R,B 两个字符。

就是贪心一下，因为需要尽量的出现 BRBRB 这种交叉的形式。

所以随便判一下就行，细节见代码。

注意要写清楚全部是 ? 的情况

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
while(T--){
    scanf("%lld",&n);
    cin>>s;s=' '+s;
    int i=0,k=0;
    for(i=1;i<=n;++i) if(s[i]!='?'){k=1;break;}
    if(k){
        for(register int j=i-1;j>=1;--j){
            if(s[j+1]=='R') s[j]='B';
            else s[j]='R';
        }
    }
    else s[1]='B'; 
    for(i=1;i<=n;++i){
        if(s[i]=='?'){
            if(s[i-1]=='R') s[i]='B';
            else s[i]='R';
        }
    }//把没有补全的地方补全
    for(i=1;i<=n;++i) cout<<s[i];puts("");
}

Cψ(｀∇´)ψ

比较简单的构造，直接放代码（压了行，不是我的正常马蜂）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
while(T--){
    scanf("%lld",&n);
    for(register int i=1;i<=n;++i) scanf("%lld",&a[i]);
    if(a[1]==1){
        printf("%lld ",n+1);
        for(register int i=1;i<=n;++i) printf("%lld ",i);puts("");continue;
    }
    if(a[n]==0){
        for(register int i=1;i<=n;++i) printf("%lld ",i);
        printf("%lld ",n+1);puts("");continue;
    }
    for(register int i=1;i<=n;++i){
        if(a[i]==0 && a[i+1]==1){
            for(register int j=1;j<=i;++j) cout<<j<<" ";
            cout<<n+1<<" ";
            for(register int j=i+1;j<=n;++j) cout<<j<<" ";
            break;
        }
    }puts("");continue;
}

D1ψ(｀∇´)ψ

给你两个独立的森林，现在每个森林都有一些边。

然后如果你要添加一条边 \((u,v)\) ，那么两个森林的 \((u,v)\) 这条边都要加上。

问在满足这两个森林仍旧是森林的条件下，最多可以加多少条边。

\(n\le1000\)。

傻逼题，并查集维护连通块然后暴力枚举所有没有联通的点对，加边即可。

D2ψ(｀∇´)ψ

同 D1 ，\(n\le 10^5\)

本次比赛最难的题。

赛时没做出来，赛后看见一个神奇的做法：

先连 \(1\) ，然后对两个森林枚举每个点看跟 \(1\) 有没有连，在这里面找点连线。

感觉有点怪但是能过（

Eψ(｀∇´)ψ

\(\gcd\) +大力容斥+DP

\(\because\gcd(a_1,a_2...a_n)=1 \Leftrightarrow\sum_{d|\gcd(a_1,a_2...a_n)}\mu(d)\).

\(\therefore\) 计算对于每个 \(d\) , \(\mu(d)\) 被算了多少次，这个直接 \(\texttt{dp}\) 即可。

也就是枚举 \(d\)，然后要计算有多少个数列满足 \(d|a_i\) 且 \(\sum_{i=1}^n a_i\le m\)

思路来自 lgsdwn(Orz lgd) 和 Silver187。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<bits/stdc++.h>
using namespace std;

#define int long long
const int si=101000;
const int mod=998244353;
int n,m;
int prime[si],mu[si];
bool vis[si];
void Mobius(int n){
    memset(vis,0,sizeof(vis));
    mu[1]=1,prime[0]=0;
    for(register int i=2;i<=n;i++){
        if(!vis[i]) prime[++prime[0]]=i,mu[i]=-1;
        for(register int j=1;j<=prime[0] && i<=n/prime[j];j++){
            vis[i*prime[j]]=1;
            if(i%prime[j]==0){
                mu[i*prime[j]]=0;
                break;
            }
            mu[i*prime[j]]=-mu[i];
        }
    }
}
int a[si],b[si];
int l[si],r[si];
int f[si],s[si];
signed main(){
    scanf("%lld%lld",&n,&m);
    Mobius(m);
    for(register int i=1;i<=n;++i){
        scanf("%lld%lld",&a[i],&b[i]);
    }
    int res=0;
    for(register int d=1;d<=m;++d){
        if(mu[d]){
            for(register int i=1;i<=n;++i){
                l[i]=(a[i]+d-1)/d,r[i]=b[i]/d;
            }
            int qwq=m/d;
            for(register int i=0;i<=qwq;++i){
                s[i]=1;
            }
            for(register int i=1;i<=n;++i){
                for(register int j=1;j<=qwq;++j){
                    f[j]=0;
                }
                for(register int j=l[i];j<=qwq;++j){
                    f[j]=s[j-l[i]];
                    if(j-r[i]-1>=0) f[j]=(f[j]+mod-s[j-r[i]-1])%mod;
                }
                s[0]=0;
                for(register int j=1;j<=qwq;++j){
                    s[j]=(s[j-1]+f[j])%mod;
                }
            }
            res=(res+mu[d]*s[qwq])%mod;
        }
    }
    res=(res+mod)%mod;
    printf("%lld\n",res);
    return 0;
}

Codeforces # 739（div3）ψ(｀∇´)ψ

Contest ID:1560

水，太水了（）

FST群的其中八位群友一起整了个活，公用一个神奇的名字的账号一起冲rk1，（当然因为F1的罚时我们是rk3）

1
Demoe,峰,tjx,tearing,lgd,bmy,monsters

我啥也没贡献（他们切题太快了）

但是因为分配的原因没有40min以内AK（呜呜）

我就只胡了一个F1和E，然后E还假了。

于是后面看到公用号AK了之后去开A题做。

后面写到 D 题就有点困了，懒得写EF12了，（反正F1F2胡出来了之后再补，E胡不出来看看题解把）

Aψ(｀∇´)ψ

一个正整数数列，从 \(1\) 开始，一直往后一个一个的增加 \(1\)，但是没有三的倍数和以三结尾的数。

然后问数列第 \(k\) 项 \(1\le k \le 1000\)。

语法题：提前for一遍，打好一千项然后直接输出，完了。

不过昨晚魔怔了，居然忘记了 % 的存在，直接写了一个：

1
2
3
inline int mod(int x,int p){
    return x<0?(x+p)-(((x+p)/p)*p):x-((x/p)*p);
}

难怪没有一分钟A。

Bψ(｀∇´)ψ

给定一个环，环上从 \(1 \sim n\) 依次站了 \(n\) 个人（\(n\) 是偶数）。

然后假设有两个人 \(x,y\) 面对着，那么 \(x,y\) 的连线就一定过圆心。

现在给你一个面对着的两个人的序号 \(a,b\) ，再另外给定一个 \(c\)，求 \(c\) 面对的人的序号，如果不存在这样的环，输出 \(-1\)。

发现两个相对点序号之差的绝对值的两倍就是一个合法的环的 \(n\) ，然后随便判一下就行。

1
2
3
4
5
int R=abs(a-b),n=R<<1;
if(c>n || (c+R>n && c<=R) || c+R==a || c+R==b || c-R==a || c-R==b || b>n || a>n){
    puts("-1");continue;
}
else printf("%lld\n",c<=R?c+R:c-R);

Cψ(｀∇´)ψ

UPD：草，这题我实际上FST了（久违了）

因为我是unofficial参赛所以没测st。

麻了。

之后有时间就补一发。

Dψ(｀∇´)ψ

发现打出 \(2^k\) 的一个表（ \(1\le k \le 31\) ）就能开始乱搞。

然后根据题目要求随便暴力匹配一下就行。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
int cal(string s,string ss){
    int res=0;
    for(register int i=0;i<(int)s.size() && res<(int)ss.size();++i){
        if(s[i]==ss[res]) ++res;
    }return res;
}
int main(){
    scanf("%d",&T);
    while(T--){
        cin>>s;
        int res=1e9;
        for(register int i=0;i<109;++i){
            res=min(res,(int)(s.size()-cal(s,a[i])*2+a[i].size()));
        }printf("%d\n",res);
    }
    return 0;
}//a是打的表。

其实正解是：贪心，确定了变成的数 \(t\) ,然后一位一位匹配。

我本来想写这个（

但我感觉打表很牛逼啊，就打了（

Eψ(｀∇´)ψ

巨大多疑惑题，不会。

F1 && F2ψ(｀∇´)ψ

害，我感觉这个F是d2a水平。

麻了，F1就是F2的特殊情况，F2大暴搜加个小剪枝优化就过了。

但是，其实有一点不太好写（）

题目要求你找到 最小的 不同数字的个数不超过 \(k\) 且这个数大于等于 \(n\) 的数。

发现F2的 \(k\) 都只有 \(10\) ,所以可以考虑大暴搜，从高到低位一个一个位地试填。

每一位从 \(1 \sim 9\) 开始填，当高位合法的时候立马向下填，直到所有位都合法。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<bits/stdc++.h>
using namespace std;

const int si=1e3+10;
int cnt[si],ans[si];
int T,k,n;
string s;

bool dfs(int now,int val,bool tag){
    if(val>k) return false;
    if(now==n && val<=k){
        for(register int i=0;i<n;++i){
            printf("%d",ans[i]);
        }puts("");
        return true;
    }
    for(register int i=tag?s[now]-'0':0;i<=9;++i){
        ++cnt[i],ans[now]=i;
        if(cnt[i]==1){
            if(dfs(now+1,val+1,tag&&i==s[now]-'0')) return true;
        }
        else if(dfs(now+1,val,tag&&i==s[now]-'0')) return true;
        --cnt[i];
    }
    return false;
}

signed main(){
    scanf("%d",&T);
    while(T--){
        for(register int i=0;i<=10;++i){
            cnt[i]=ans[i]=0;
        }
        cin>>s;scanf("%d",&k);
        n=(int)s.size();
        if(!dfs(0,0,1)){
            printf("10");
            for(register int i=2;i<k;++i){
                printf("%d",i);
            }puts("");
        }
    }
    return 0;
}

Atcoder Beginning Contest 215ψ(｀∇´)ψ

Contest ID：abc_125

部分补题有参 考

A & Bψ(｀∇´)ψ

语法题。

B的话需要手写 \(\log_2\)。

自带的 \(\log_2\) 一旦上了 \(2^{59}\) 左右就会出事，所以建议手写下面的：

1
2
3
4
5
6
7
unsigned long long Log2EX(unsigned long long x)  {    
    unsigned long long i=0;
    for(i=64;i>=0;i--){
        if(1==(x>>i)&0x1) break;
    }
    return i;  
}

Cψ(｀∇´)ψ

问你一个字符串按字典序的第 \(k\) 个排列。

水题，使用 next_permutation 即可。、

这个东西可以返回下一个排列，但是如果要全排列的话一定要先 sort

1
2
3
4
5
6
    int cnt=0;
    sort(s.begin(),s.end());//一定要sort
    do{
        ++cnt;
        if(cnt==n) cout<<s<<endl;
    }while(next_permutation(s.begin(),s.end()));

其实完全可以直接 break ，不过没什么影响。

Dψ(｀∇´)ψ

给一个序列，要求你找出所有在值域 \([1,m]\) 之间的 \(k\)，满足 \(k\) 和序列里的所有数都互质。

考虑质因数分解，对每个数分解，对质数求并。

那么考虑每一个 \(i\)，同样质因数分解即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<bits/stdc++.h>
using namespace std;

#define int long long
const int si=1e5+10;
int n,m,cnt,res;
int a[si],prime[si];
bool vis[si],ans[si];
inline int mod(int x,int p){
    return x<0?(x+p)-(((x+p)/p)*p):x-((x/p)*p);
}
int tp[si],pos[si];
void Euler(int n){
    for(register int i=2;i<=n;++i){
        if(tp[i]) continue;
        prime[++cnt]=i,pos[i]=cnt;
        for(register int j=(i<<1);j<=n;j+=i){
            tp[j]=1;
        }
    }
}

signed main(){
    cin>>n>>m;
    Euler(m);
    for(register int i=1;i<=n;++i){
        cin>>a[i];
    }
    for(register int i=1;i<=n;++i){
        for(register int j=1;j<=cnt && 1ll*prime[j]*prime[j]<=a[i];++j){
            if(!mod(a[i],prime[j])) vis[j]=true;
            while(!mod(a[i],prime[j])) a[i]/=prime[j];
        }
        if(a[i]!=1) vis[pos[a[i]]]=true;
    }
    memset(ans,true,sizeof ans);
    for(register int i=1;i<=cnt;++i){
        if(vis[i]) for(register int j=prime[i];j<=m;j+=prime[i]) ans[j]=0;
    }
    for(register int i=1;i<=m;++i){
        if(ans[i]) res+=1;
    }cout<<res<<endl;
    for(register int i=1;i<=m;++i){
        if(ans[i]) cout<<i<<endl;
    }
    return 0;
}

Eψ(｀∇´)ψ

题面很怪，这里直接给一个简化版

给定一个字符串，选择一个子序列出来，满足同一种字符在这个子序列里面都在一段里，求方案数对 \(998244353\) 取模。

也就是不会有 BBABB 这种情况。

字符种类小于十，字符串长度不超过一千。

一个比较板子的状压？

考场没调出来。

设 \(f_{i,msk,t}\) 表示考虑前 \(i\) 场比赛，当前状态是 \(msk\)，最后打的一场的种类是 \(t\)。

且第 \(i\) 场比赛的种类是 \(k\)。

所以有转移方程：

\(\begin{cases}f_{i,msk,t}=f_{i-1,msk,t}\\f_{i,msk,t}=f_{i,msk,t}+f_{i-1,msk,t},(t=k)\\f_{i,u\ \text{or}\ 2^{k},k}+=f_{i-1,u,t}\\f_{i,2^{k},k}=f_{i,2^{k},k}+1\end{cases}\)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
using namespace std;

const int Mod=998244353;
const int si=1028;
int n,f[si][si][10];
inline int mod(int x){
    return x<0?(x+Mod)-(((x+Mod)/Mod)*Mod):x-((x/Mod)*Mod);
}
string s;

int main(){
    cin>>n>>s;s=' '+s;
    for(register int i=1;i<=n;++i){
        int k=s[i]-'A';
        for(register int msk=1;msk<=1024;++msk){
            for(register int j=0;j<10;++j){
                f[i][msk][j]=f[i-1][msk][j];
                if(j==k) f[i][msk][j]=mod(f[i][msk][j]+f[i-1][msk][k]);
            }
        }
        for(register int msk=1;msk<=1024;++msk){
            if(msk&(1<<k)) continue;
            for(register int j=0;j<10;++j){
                f[i][msk|(1<<k)][k]=mod(f[i][msk|(1<<k)][k]+f[i-1][msk][j]);
            }
        }
        f[i][1<<k][k]=mod(f[i][1<<k][k]+1);
    }   
    int res=0;
    for(register int i=1;i<=1024;++i){
        for(register int j=0;j<10;++j){
            res=mod(f[n][i][j]+res);
        }
    }cout<<res<<endl;
    return 0;
}

Fψ(｀∇´)ψ

给定 \(n\) 个点，定义两个点对 \((x_1,y_1),(x_2,y_2)\) 的距离为 \(\min (|x_1-x_2|,|y_1-y_2|)\)。

求任意两个点对之间距离的最大值。

\(n\) 在 \(2\times 10^5\) 级别，坐标都是 \(10^9\) 级别。

第一反应是直接暴力，然后发现是 \(\text{O}(n^2)\) 级别，爆炸。

然后有一个分别从 \(x,y\) 轴大力维护区间信息的做法，然后发现不可做。

于是在极度绝望的时候，我看见了二分。

我觉得这个东西也许可以转化为判定性问题。

假设 \(\min (|x_1-x_2|,|y_1-y_2|) \ge k\)

那么很明显， \(|x_1-x_2| \ge k ,|y_1-y_2| \ge k\)

然后这东西很明显具有单调性，现在考虑怎么二分 \(k\)。

首先你先对 \(x\) 升序排序方便处理。

如果在 \(k\) 可行的前提下的话，就假设有一个点 \((x_i,y_i)\)。

然后再假设 \(y\) 最小的点是 \((x.y)\)（这里稍微贪心了一下）。

然后如果说 \(x_i-x \ge k\) 了，那么很明显，因为 \(k\) 是可行的，所以 \(y_i-y \ge k\) 也就是有：

\(A\begin{cases}x_i-k \ge x\\y_i-k \ge y\end{cases}\)

但是你发现可能会有这种情况：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
y
\
|           ·(xx,ymax)
|         
|
|
|
|
|     ·(x_i,y_i)
|
| ·(x,ymin)
---------------------------\x

也就是说 \(y\) 的最大值可能比 \(y\) 的最小值做出的贡献更大，所以最大的 \(y\) 也要跑一遍。

同理就是 \(B \begin{cases}x_i+k \le x\\y_i+k \le y\end{cases}\)

所以我们在二分的里面去check \(A,B\) 这两个条件是否有至少一个成立就可以了。

然后具体来说就是按照 \(x\) 排一个序，然后进行分段双指针。

以 \(i\) 为右端点， \(j\) 为左端点，那么什么时候我们可以右移左端点？

就是 \(j+1\) 这个点，他的横坐标和 \(i\) 的差值大于等于这个 \(k\) 。

那么显然如果我在 \(i\) 处做到了 \(j\) ，那么所有 \(i\) 右边的点和 \(j\) 的组合都是合法的，所以这个 \(j\) 他就永远是合法的。

那么我们就可以记录一下已做到的 \(j\) 他的纵坐标的最大值和最小值，和每一个进去的 \(i\) 的纵坐标减一减，

如果纵坐标之差要大于等于 \(k\) ，而横坐标我们已经证明了他的差值必定大于等于 \(k\) ，那么这个 \(k\) 就肯定是成立的。

但是这个题，如果只遍历一次那么答案可能会被漏掉，所以还得从右往左遍历一遍，此时 \(j\) 是右端点， \(i\) 是左端点。

因为不可抗力因素让我总是奇怪的WA，所以对着tutorial 改了一些地方

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <bits/stdc++.h>
using namespace std;

#define xi first
#define yi second
int n;

int main(){
    cin>>n;
    vector<pair<int,int> >v(n);
    for(register int i=0;i<n;++i){
        cin>>v[i].xi>>v[i].yi;
    }
    sort(v.begin(),v.end());
    int l=0,r=1e9+7;
    while(r-l>1){
        int mid=(l+r)>>1;
        queue<pair<int,int> >q;
        bool f=false;
        int mi=1e9+7,mx=0;
        for(auto p:v){
            while(!q.empty()){
                int x=q.front().xi,y=q.front().yi;
                if(x>p.xi-mid) break;
                mi=min(mi,y),mx=max(mx,y);q.pop();
            }
            if(mi<=p.yi-mid || mx>=p.yi+mid) f=true;
            q.push(p);
        }
        if(f) l=mid;
        else r=mid;
    }
    cout<<l<<endl;
    return 0;
}

````

### G & H
>不会

## Nowcoder PJ 28

Contest ID：`11235`

出题人是FST群群友： CSP-Sept ~~~

很有感觉，开场一个小时只过了A，然后最后半小时直接AK，刺激。

另外牛客的小白月赛36就不写了，只有E感觉比较有价值。

### A

发现这个移动是有周期性的，而且移动次数是 $10^{18}$。

所以就是个诈骗题（

直接把移动次数模上字符串长度，然后从这个余数 $+1$ 位开始输出，然后在从第 $1$ 位一直输出到余数这一位即可。

1minAC（

```cpp

#include<bits/stdc++.h>
using namespace std;

#define int long long
string s;
int n,x;
signed main(){
    cin>>n>>x;
    cin>>s;s=' '+s;
    int r=x%n;
    for(int i=r+1;i<=n;++i) cout<<s[i];
    for(int i=1;i<=r;++i) cout<<s[i];
}

Bψ(｀∇´)ψ

最后才AC的题。

这个是在矩阵上求 \(y\) 轴方向的 \(\texttt{LIS}\) ，然后矩阵最大 \(5\times10^3 \times 10^3\)

听何神说有一种 \(\text{O}(NK)\) 的做法，但是我不会。

考虑设 \(f_i\) 表示长度为 \(i\) 的 \(\texttt{LIS}\) 的最小结尾，这样子方便去转移。

然后发现这就是 \(\text{O} (n \log n)\) 求 \(\texttt{LIS}\) 的状态。

所以我们考虑直接多循环一次然后套上板子。

然后你发现在

1
2
1 5
1 2 3 4 5

的这个数据上你会输出 \(5\) 。

为啥那？

因为我们的做法会导致重复覆盖。

就和01背包一个道理，所以reverse一下就好了。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>
using namespace std;

#define int long long

const int si=1e3+10;
int k,n;
#define pb push_back
vector<int>v[si];
int f[si];
int nlogn_lis(){
    int len=0;
    f[0]=-1;
    for(int i=1;i<=n;++i){
        for(int j=0;j<(int)v[i].size();++j){
            if(v[i][j]>f[len]) f[++len]=v[i][j];
            else *lower_bound(f,f+len,v[i][j])=v[i][j];
        }
    }
    return len;
}

signed main(){
    scanf("%lld%lld",&k,&n);
    for(int i=1;i<=n;++i){
        for(int j=1,q;j<=k;++j){
            scanf("%lld",&q);
            v[i].pb(q);
        }
        reverse(v[i].begin(),v[i].end());
    }
    printf("%lld",nlogn_lis());
}

Cψ(｀∇´)ψ

大原题，洛谷上的“图的遍历”就是基本一样的。

我本来写的是缩点+DP，但是挂了好多发。

突然想起可以“正难则反”的思想做，对于每一个节点能到达的点，

记录可以到这个点所有点的编号的最小值。

然后建反图跑一遍就行。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include<bits/stdc++.h>
using namespace std;

const int si=1e5+10;
int n,m,f[si];
vector<int>g[si];
vector<int>v;
void dfs(int x,int d){
    if(f[x]) return;
    f[x]=d;
    for(int i=0;i<g[x].size();i++) dfs(g[x][i],d);
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1,u,vv;i<=m;i++){
        scanf("%d%d",&u,&vv);
        g[vv].push_back(u);
    }
    for(int i=1;i<=n;i++) dfs(i,i); 
    for(int i=1;i<=n;i++) v.push_back(f[i]);
    sort(v.begin(),v.end());
    v.erase(unique(v.begin(),v.end()),v.end());
    for(int i=0;i<(int)v.size();++i) cout<<v[i]<<" ";
    return 0;
}

Dψ(｀∇´)ψ

很精妙的DP。

发现正着做很麻烦，所以我们把序列倒过来，发现这东西很平凡。

设 \(f_i\) 表示倒过来之后从 \([1,i]\) 这个区间全部吃完的最大值。

然后考虑 \(a_i\) ，他不是这个区间最后一个吃的就是第一个吃的。

所以处理出 \(\Delta\) 的前缀和，所以分两种情况转移即可。 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std;

#define int long long
const int si=2e5+10;
int n;
int a[si],delta[si];
int f[si],sum[si];
inline int cal(int pos){ 
    return ((pos-1)*delta[pos])+a[pos];
}
signed main(){
    scanf("%lld",&n);
    for(int i=n;i>=1;--i){
        scanf("%lld",&a[i]);
    }
    for(int i=n;i>=1;--i){
        scanf("%lld",&delta[i]);
    }
    for(int i=1;i<=n;++i){
        sum[i]=sum[i-1]+delta[i],f[i]=-10737418190000000;
    }
    f[1]=a[1];
    for(int i=2;i<=n;++i){
        f[i]=max(f[i-1]+sum[i-1]+a[i],f[i-1]+cal(i));
    }
    return printf("%lld",f[n]),0;
}

Atcoder Beginning Contest 216ψ(｀∇´)ψ

Contest ID:abc_216

开学前一天晚上有连着的ABC和一场CF，可以上大分力！。

因为明天就开学了所以就先咕这不写。

到时候课表出来之后找竞赛课时间上来机房写。

G 是个裸的差分约束，可惜没写，不然就只差 H 了。

最近打的最好的一次ABC（可能是水了？）

A & Bψ(｀∇´)ψ

都是语法题。

A的话特判一下，B的话整个 map<pair<string,string>,bool> 就过了

Cψ(｀∇´)ψ

很妙，你有 \(120\) 次操作，可以把给定的值加一，或者把值乘2.

问构造一个 \(2^{64}\) 以内的整数的方案。

发现 \(120\) 次完全够了。\(120\) 以内的话就直接一直加一就可以。

反之如果 \(n\) 是奇数，减一然后一直除二，然后如果又是奇数那就重复。

直到 \(n\) 为 \(0\) 即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<bits/stdc++.h>
using namespace std;

long long n;

int main(){
    scanf("%lld",&n);
    if(n<=120){
        for(register int i=1;i<=n;++i){
            putchar('A');
        }return 0;
    }
    else{
        string s;bool f=false;
        if(n&1) n-=1,f=true;
        while(n){
            if(n%2==0) n/=2,s='B'+s;
            if(n&1) n-=1,s='A'+s;
        }
        if(f) s+='A';
        cout<<s<<endl;
    }
}

Dψ(｀∇´)ψ

D 的话就直接开一个 deque 和一个 queue 模拟就可以了。

当然你可以利用拓扑的思想直接建图然后跑一个拓扑。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#define int long long
int n,m,sz[MAXN],num;
pair<int,int>pos[MAXN];
deque<int>a[MAXN];
queue<int>q;
void del(int x){
    a[x].pop_front();
    if(a[x].size()){
        int u=a[x].front();
        if(pos[u].fr==0) pos[u].fr=x;
        else pos[u].se=x,q.push(u),num++;
    } 
}
signed main(){
    cin>>n>>m;
    for(register int i=1;i<=m;++i){
        cin>>sz[i];
        for(register int j=1;j<=sz[i];++j){
            int tmp;cin>>tmp;
            a[i].pb(tmp);
        }
    }
    for(register int i=1;i<=m;++i){
        int u=a[i][0];
        if(pos[u].fr==0) pos[u].fr=i;
        else pos[u].se=i,q.push(u),num++;
    }
    while(!q.empty()){
        int u=q.front();q.pop();
        del(pos[u].fr),del(pos[u].se);
    }
    if(num==n) puts("Yes");
    else puts("No");
    return 0;
}

Eψ(｀∇´)ψ

大毒瘤贪心，建一个大根堆然后把所有东西丢进去维护。

然后每次把堆顶 \(top\) 之后，把 \(top-1\) 扔进去就可以。

这样子还不太够。需要稍微优化一下，就自己理解吧。

这个东西我没做出来，那份代码是有个人要我帮他吃罚时交的（

Fψ(｀∇´)ψ

DP，首先把 \(a\) 降序排一遍，然后对于每一个 \(j \in [1,n]\) ，假设 \(f_j\) 表示选上 \(a_j\) ，不管其他的怎么选所得到的解。

然后你发现 \(a_j\) 要满足 \(\ge b_k + \sum\limits_{i \subset S} b_i,S=\{k+1,k+2,...,n\}\)

这个东西可以背包，不过需要前缀和优化。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
    const int limit=5000;
    sort(q+1,q+1+n);f[0][0]=1;
    for(register int i=1;i<=n;++i){
        for(register int j=0;j<=limit;++j){
            f[i][j]=f[i-1][j];
        }
        for(register int j=q[i].b;j<=limit;++j){
            f[i][j]+=f[i-1][j-q[i].b],mod(f[i][j]);
        }
    }
    for(register int i=0;i<=n;++i){
        for(register int j=1;j<=limit;++j){
            f[i][j]+=f[i][j-1],mod(f[i][j]);
        }
    }
    for(register int i=1;i<=n;++i){
        if(q[i].a<q[i].b) continue;
        ans+=f[i-1][q[i].a-q[i].b],mod(ans);
    }printf("%lld\n",ans);

Gψ(｀∇´)ψ

裸的差分约束。

但是写挂了呜呜呜

Deltix Round, Summer 2021 (CF1556)ψ(｀∇´)ψ

Contest ID:CF1556

这场极度毒瘤啊啊啊啊，D出了个交互+大毒瘤构造。

然后E我开始先写的暴力，然后发现要用RMQ优化，于是写了一个ST表。

然后赛后CFM给了我一组数据把我的错误做法叉掉了。

但是并没有在ST里面出现ovo，我当时以为要FST了，于是极度生气。

早上起来发现却上分了，因为E的systest太弱了！

然后趁走之前改了一下，把错误做法改对了，很有感觉！

比较可惜的就是没上CM，呜呜，要是D交互部分不写挂就上CM了呜呜。

题解的话之后再来写，今天开学了没时间呜呜呜。

（听说 tourist 只有rk22，毒瘤！（其实是因为他最后面两道似乎因为什么没做）

这下面空着的都是没时间写的（ABC的都是到学校之后溜去机房写的）

Aψ(｀∇´)ψ

猜了个结论过了。

发现如果 \(c,d\) 的奇偶性不同，肯定不能构造。

排除无解之后，如果全是 \(0\) 就不用构造，然后 \(c=d\) 就只需要一步。

如果 \(c \not= d\) 的话，第一步构造 \([c,d]\) 这个区间的中位数，然后再向上向下构造一次即可。

BCDEψ(｀∇´)ψ

咕着，不想写了。

FGH...ψ(｀∇´)ψ

因为是 div1+div2,所以后三题现在真的不会qwq

Codeforces Round #747ψ(｀∇´)ψ

Contest ID : 1594

很久没打了，现在停课期间有时间那么就打了一下。

但是手感很不好，A 傻逼了，B傻逼了，E1傻逼了。

同机房第一次打的都吊打我。

只有 ACD /kk

Aψ(｀∇´)ψ

构造一个区间 \(l,r\) 使得区间和为 \(n\)。

因为可以是负数，所以直接 \([1-n,n]\)。

Bψ(｀∇´)ψ

大简单题，傻逼了。

问你由 \(n\) 的整数次幂组成数的第 \(k\) 大。

可以用二进制做。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include<bits/stdc++.h>
using namespace std;

#define int long long
int T;
int n,k;
const int p=1e9+7;

signed main(){
    scanf("%lld",&T);
    while(T--){
        int res=0;
        int delta=1;
        scanf("%lld%lld",&n,&k);
        for(register int j=1;j<=32;++j){
            if(k&(1<<(j-1))) res=(res+delta)%p;
            delta*=n,delta%=p;
        }
        printf("%lld\n",res);
    }
    return 0;
}

Cψ(｀∇´)ψ

要求你把字符串所有位变成给定的字符 \(ch\)

每次可以选择一个数 \(x\) ，对于所有的 \(s[i],x \not| \ \ i\)，令他变成 \(ch\)。

问最小操作次数。

发现最多只需要两次 : \(x=n-1.x=n\)。

然后不用动了直接特判 \(0\)。

然后考虑用 \(i\times j\) 这样类似欧拉筛的办法去判断是否能一次干完即可。

Dψ(｀∇´)ψ

是个并查集，有点像食物链那一题。

内鬼只会说假话，好人只会说真话。

然后每个人会指认谁是什么身份。

问你最多有多少内鬼。

考虑分类讨论。

如果 A 说 B 是好人，那么 A 和 B 的身份肯定是一样的。

因为如果 A 是好人，说真话，那么 B 也是好人。

反之 A 是内鬼 ，说假话，那么 B 也是内鬼。

如果 A 说 B 是内鬼，那么也有两种情况。

如果 A 是好人，那么 B 就是内鬼。

如果 A 是内鬼，那么 B 就是好人 。

然后我们就考虑利用并查集维护他们的关系，然后顺便进行处理即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<bits/stdc++.h>
using namespace std;

#define int long long 
int T;
const int si=2e5+10;
int pa[si],dis[si],siz[si],res[si];
bool vis[si];
int n,m,ans;
int root(int x){
    if(pa[x]==x) return pa[x];
    int fa=root(pa[x]);
    dis[x]^=dis[pa[x]];
    return pa[x]=fa;
}
inline void Union(int u,int v,int ru,int rv,int w){
    dis[ru]=w xor dis[u] xor dis[v];
    siz[rv]+=siz[ru],pa[ru]=rv;
}
inline void init(int n){
    for(register int i=1;i<=n;++i){
        pa[i]=i,dis[i]=0,siz[i]=1;
        vis[i]=false,res[i]=0;
    }
}

signed main(){
    scanf("%lld",&T);
    while(T--){
        scanf("%lld%lld",&n,&m);
        init(n);
        bool print_ck=true;
        string sta;
        for(register int i=1;i<=m;++i){
            int u,v,tet;
            scanf("%lld%lld",&u,&v);
            cin>>sta;
            if(sta[0]=='c') tet=0;
            else tet=1;
            int ru=root(u),rv=root(v);
            if(ru==rv){
                if((dis[u] xor dis[v])!=tet){
                    if(print_ck) puts("-1");
                    print_ck=false;
                }
            }
            else Union(u,v,ru,rv,tet);
        }
        if(!print_ck) continue;
        for(register int i=1;i<=n;++i){
            int ri=root(i);
            if(dis[i]==0) res[ri]++;//pa[i]?
        }
        ans=0;
        for(register int i=1;i<=n;++i){
            if(root(i)!=i) continue;
            ans+=max(res[i],siz[i]-res[i]);
        }
        printf("%lld\n",ans);
    }
    return 0;
}

E1ψ(｀∇´)ψ

大简单题，傻逼了。

给你一个完全二叉树，让它涂色，每种涂色有限制。

答案就是 \(6 \times 4^{2^{k}-2}\)。

快速幂即可。

1
2
3
4
5
6
7
8
9
signed main(){
    int n;
    scanf("%lld",&n);
    int k=(1ll<<n)-2ll;//一定要写 1ll,不然 1 会默认 int 导致爆炸。
    int ans=qpow(4ll,k,p);
    ans=(ans*6ll)%p;
    printf("%lld\n",ans);
    return 0;
}

E2 & Fψ(｀∇´)ψ

还不会

Atcoder Beginning Contest #222ψ(｀∇´)ψ

Contest ID: abc_222

A & Bψ(｀∇´)ψ

语法题就不提了

Cψ(｀∇´)ψ

题目理解可能比较困难（

大概是让你在某种规则下判断石头剪刀布的输赢之类的。

直接大模拟即可。

Dψ(｀∇´)ψ

给你两个不降的序列 \(a,b\)。

要求你构造一个序列 \(c\) 使得对于任意的 \(i\) 都有 \(c_i \in [a_i,b_i]\)

值域 \(3000\) ，长度 \(3000\)。

一个比较基础的 dp。

设 \(f_i\) 表示考虑到第 \(i\) 个位置的时候的方案数。

然后你发现因为 \([a_i,b_i],[a_{i+1},b_{i+1}]\) 是可能有重合的。

你需要去枚举 \(c_i\) 到底选什么的情况。

发现值域乘上长度也只有 \(9\times 10^6\) ，所以考虑一个朴素的 dp。

设 \(f_{i,j}\) 表示考虑到第 \(i\) 个位置时，\(c_i=j\) ，的满足条件的序列总数。

那么方程就是

\[f_{i,j}=\begin{cases}\sum\limits_{k=0}^{j}f_{i-1,k} & i \ge 1,j\in [a_i,b_i]\\1 & i=j=0\\0 & \text{otherwise.}\end{cases}\]

但是发现这样子是 \(\text{O}(nm^2)\) 的（\(m\) 是值域），所以考虑优化。

第一种情况你发现是个前缀和，所以我们考虑使用前缀和优化这玩意儿。

令 \(S_{i,j}=\sum\limits_{k=0}^{j}f_{i,k}\)，然后用前缀和的形式把 \(S\) 写出来。

然后因为前缀和是个递推式，所以你就可以 \(\text{O}(nm)\) AC本题。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
    for(register int i=a[1];i<=b[1];++i){
        f[1][i]=1;
    }sum[0]=f[1][0];
    for(register int i=1;i<=si-10;++i){
        sum[i]=sum[i-1]+f[1][i];
    }
    for(register int i=2;i<=n;++i){
        for(register int j=a[i];j<=b[i];++j){
            f[i][j]=sum[j];
        }
        sum[0]=f[i][0];
        for(register int j=1;j<=si-10;++j){
            sum[j]=(sum[j-1]+f[i][j])%p;
        }
    }int ans=0;
    for(register int i=a[n];i<=b[n];++i){
        ans=(ans+f[n][i])%p;
    }printf("%d\n",ans%p);

E Fψ(｀∇´)ψ

俩DP，一个背包+树上差分一个换根，但是不会写呜呜

Gψ(｀∇´)ψ

原题：202. 最幸运的数字 - AcWing题库

3696 -- The Luckiest number (poj.org)

Hψ(｀∇´)ψ

不会

Edu #115ψ(｀∇´)ψ

Contest ID : 1598

特意提早回学校机房打的。

机房打的人不是很多，不过这场确实有点毒瘤？

G 题全场只有两个人AC，tourist 冲了一个小时。

F 题 MZX神想了半小时没想出来，CFM 和 45d 全部T飞

何神的 D 和 E被叉爆了，YL 的 D 读错题了。

不过 wqs 神 随便乱切！！orz

Aψ(｀∇´)ψ

大特判题，只要有一对 \(a_i=b_i=1\) 那么无解。

Bψ(｀∇´)ψ

还是大特判题。

你就考虑枚举所有可能点对 \((i,j)\)。

然后分 \((0,0)(0,1)(1,0)\) 的情况讨论即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<bits/stdc++.h>
using namespace std;

#define int long long
int T,n;
const int si=1e3+10;
int a[si][10];

signed main(){
    scanf("%lld",&T);
    while(T--){
        scanf("%lld",&n);
        for(register int i=1;i<=n;++i){
            for(register int j=1;j<=5;++j){
                scanf("%1lld",&a[i][j]);
            }
        }
        bool f=false;
        for(register int i=1;i<5;++i){
            for(register int j=i+1;j<=5;++j){
                int cnt=0,cntt=0,cnttt=0;
                for(register int k=1;k<=n;++k){
                    if(a[k][i]==1 && a[k][j]==0) ++cnt;
                    else if(a[k][i]==0 && a[k][j]==1) ++cntt;
                    else if(a[k][i]==1) ++cnttt;
                }
                if(cnt+cntt+cnttt>=n && cnt+cnttt>=(n>>1) && cntt+cnttt>=(n>>1)){
                    f=true;break;
                }
                if(!f) continue;
            }
        }
        if(f) puts("YES");
        else puts("NO");
    }
    return 0;
}

Cψ(｀∇´)ψ

问你对于给定的序列，有多少种去掉两个数 \(a_i,a_j\) 的方案（\(i<j\)）使得序列平均数不变。

直接用个 unordered_map 来处理每一个数的出现次数。

你发现要有解，那么平均数肯定是 .0 或者 .5 结尾。

说白了 \(2sum\ \text{mod}\ n=0\)。

然后为了防止重复的情况，我们这样子写：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std;

#define int long long
int T;
const int si=2e5+10;
int n,a[si];
long double k=0;
unordered_map<int,int>mp;

signed main(){
    scanf("%lld",&T);
    while(T--){
        scanf("%lld",&n);
        mp.clear();
        int sum=0;
        for(register int i=1;i<=n;++i){
            scanf("%lld",&a[i]);sum+=a[i];
        }
        if((sum<<1ll) % n){
            puts("0");
            continue;
        }
        int kk=sum*2/n;
        int res=0;
        for(register int i=1;i<=n;++i){
            res+=mp[kk-a[i]];mp[a[i]]++;
        }
        printf("%lld\n",res);
    }
    return 0;
}// 用 map 应该可以，我这个被人卡了呜呜

我们可以先把序列看作升序排序的。

然后你发现匹配的两个端点是关于平均数的位置近似对称的。

这样子写会让每一个点对的答案都在遍历到位置靠后的那个点的时候才更新。

那么就避免了点对的重复计算（样例一的 8 8 8 8 的情况也能完美解决）。

Dψ(｀∇´)ψ

大数学题（容斥+组合）

问给定的两个序列 \(a,b\) 中选出三个位置 \(i,j,k\) 使得下列条件至少有一个成立：

  • \(a[i] \not= a[j] \not= a[k]\)
  • \(b[i] \not= b[j] \not= b[k]\)

有多少种方案。

考虑把任意选三个位置的方案数算出来：\(|U|=\text{C}^{3}_{n}=\dfrac{n\times(n-1)\times(n-2)}{6}\)

然后你要去掉的就是两种都不满足的方案数。

我们考虑分别记录 \(a,b\) 当中的每个数分别在自己所处的序列当中出现的次数 \(cnta,cntb\)。

你发现你要处理的不满足条件的就是“有相等”的情况。

然后对于每一个条件，你都要处理“有两个相同，有三个相同”的情况。

所以这里就又是容斥，对于 \(a\) （\(b\) 同理），我们设位置 \(i,j\) 出现相同的情况集合为 \(A\) ，\(i,k\) 相同的情况集合为 \(B\) ，\(j,k\) 相同的情况集合是 \(C\)，那么我们要求的就是 \(A \cup B \cup C\) ，这里就可以用容斥算。

考虑你现在扫到位置 \(i\)，那么在 \(a\) 当中，我们发现这个位置他出现了 \(cnta_{a_i}\) 次，在 \(b\) 里面出现 \(cntb _{b_i}\) 次，

那么根据乘法原理，在不管重不重复计算的情况下就有 \(cnta_{a_i} \times cntb_{b_i}\) 种可能。

我们考虑对这个东西容斥一下来去重。

因为你在其他地方还可能再取到这个位置的数字所代表的情况，而且每扫到一个 \(a_i\) 或者 \(b_i\) 就会多算一次/

那么我们先给他们减去 \(cnta_{a_i}+cntb_{b_i}\)，

然后你发现这个位置本来的那一个情况被多减了，所以我们再加上 \(1\)。

我们把每一个位置所能给出的贡献写出来：\(S_i=cnta_{a_i}\times cntb_{b_i}-cnta_{a_i}-cntb_{b_i}+1\)。

所以根据加法原理，我们要求的都不满足的情况就是 \(\sum\limits^n_{i=1}S_i=\sum\limits^{n}_{i=1}[(cnta_{a_i}-1) \times (cntb_{b_i}-1)]\)。

所以答案是 \(\text{C}^3_n-\sum\limits^{n}_{i=1}[(cnta_{a_i}-1) \times (cntb_{b_i}-1)]\)。

Eψ(｀∇´)ψ

题意自己看原题。

发现每次修改格子只会影响 \(n\) 条路径，所以你就每次维护一下。

然后就可以 \(\text{O}(nq)\) 做。

F & Gψ(｀∇´)ψ

冲不动，太难力/kk

Technocup 2022 - Elimination Round 2ψ(｀∇´)ψ

Contest Id:1584,1588,1589

当经历过一些变化之后打的第一次 CF。

虽然是 VP。

另外二号机房只有我一个人想题的感觉确实舒服。

1589A,1584Aψ(｀∇´)ψ

构造方程 \(\dfrac{x}{u}+\dfrac{y}{v}=\dfrac{x+y}{u+v}\) 的解，其中 \(u,v\) 给定且 $(x,y)\not= (0,0) $

稍微乱解一下可以发现，\(x=-u^2,y=v^2\) 即可。

1589B,1584Bψ(｀∇´)ψ

猜的结论，我觉得只要 \(n\times m\) 能被 \(3\) 整除那么可以全部切成 \(1 \times 3\) 或者 \(3 \times 1\) 的。

然后其他情况推一下可以发现是 \(\dfrac{n\times m}{3} +1\)。

1589C,1584C,1588Aψ(｀∇´)ψ

考虑先对 \(a,b\) 排序。

然后倒着从大到小枚举，判断下列条件是否不成立即可。

b[i]-a[i]>1 || b[i]-a[i]<0

成立输出 NO 跑路，反之循环完了输出 YES 即可。

Dψ(｀∇´)ψ

交互题，我比较Lazy所以明天做。

最后更新: May 9, 2023