ATC & CF 选做(22Nov,22Dec)
十一 & 十二月 CF AT 丢人做题记录
大部分翻译来自洛谷。
ABC277E - Crystal Switches
给你一张简单无向图,每个边 \((u_i, v_i)\) 有一个属性 \(a_i\) 。
其中如果 \(a_i\) 为 \(1\) 表示这条边是可以通行的,否则是不可通行的。
有 \(K\) 个特殊点,如果你处于这个特殊点,你可以进行一次转换,使得所有的 \(a_i\) 取反。
问你从 \(1 \to n\) 的最短路(无解则答案为 -1)。
\(2\le n \le 2e5, 1\le m \le 1e5, 0\le K \le n\) 。
呃呃,感觉是比较板子的分层图最短路。
就是你看到有一些边要在特殊情况下才能通行或者这些边的边权会改变之类的时候,就考虑把边分类。
并且拆点,把图分成多层,如果遇到可以进行不同层转移的节点(比如本题中的特殊点),就在不同层之间连边(这条边的代价取决于在层之间转移的代价)。
之后问题就可以转化成普通的最短路问题了。
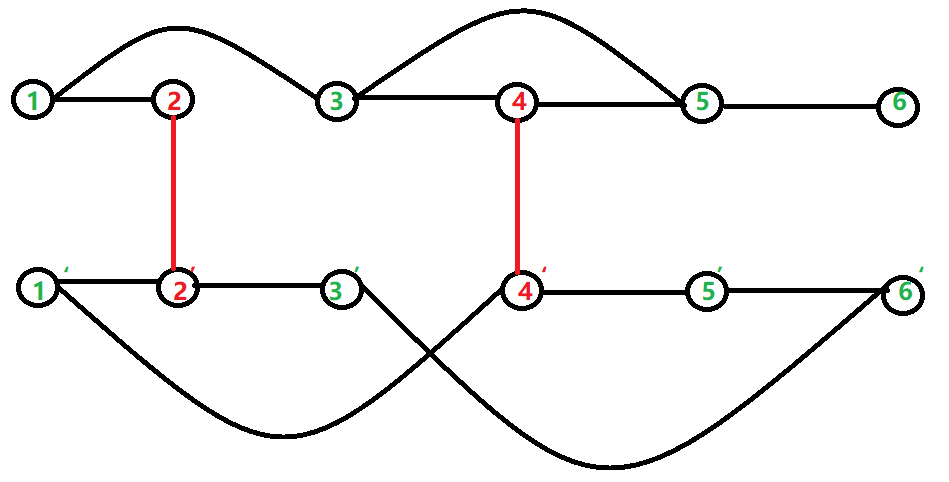
对应到这道题上就是考虑把 0/1 状态的边分开连,同层边的边权设置为 \(1\) ,因为我们转换一次不耗费任何代价,所以不同层之间的边的边权是 \(0\) 。
类似这样:
然后连完边直接求最短路即可。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65 // author : black_trees
#include <cmath> #include <queue> #include <cstdio> #include <utility> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; const int si = 2e5 + 10 ; int n , m ; int tot = 0 , head [ si << 1 ]; struct Edge { int ver , Next , w ; } e [ si << 2 ]; inline void add ( int u , int v , int w ) { e [ tot ] = ( Edge ){ v , head [ u ], w }, head [ u ] = tot ++ ; } std :: priority_queue < std :: pair < int , int > > q ; bool vis [ si << 1 ]; int dis [ si << 1 ]; void dijkstra ( int s ) { memset ( vis , false , sizeof vis ), memset ( dis , 0x3f , sizeof dis ); dis [ s ] = 0 , q . push ({ dis [ s ], s }); while ( ! q . empty ()) { int u = q . top (). second ; q . pop (); if ( vis [ u ]) continue ; vis [ u ] = true ; for ( int i = head [ u ]; ~ i ; i = e [ i ]. Next ){ int v = e [ i ]. ver , w = e [ i ]. w ; if ( dis [ v ] > dis [ u ] + w )
dis [ v ] = dis [ u ] + w , q . push ({ - dis [ v ], v }); } } } int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); memset ( head , -1 , sizeof head ); int K ; cin >> n >> m >> K ; for ( int i = 1 ; i <= m ; ++ i ) { int u , v , w ; cin >> u >> v >> w ; if ( w == 0 ) add ( u + n , v + n , 1 ), add ( v + n , u + n , 1 ); if ( w == 1 ) add ( u , v , 1 ), add ( v , u , 1 ); } for ( int i = 1 ; i <= K ; ++ i ) { int gt ; cin >> gt ; add ( gt , gt + n , 0 ), add ( gt + n , gt , 0 ); } dijkstra ( 1 ); int ans = min ( dis [ n ], dis [ n + n ]); if ( ans < 0x3f3f3f3f ) cout << ans << endl ; else cout << "-1" << endl ; return 0 ; }
ABC279D - Freefall
给定两个数 \(a\) ,\(b\) (\(1 \le a, b \le 10^{18}\) ),求出 \(\min\limits_{g = 1}^\infty\{b \times (g - 1) + \frac{a}{\sqrt{g}}\}\) 。精度误差不超过 \(10^{-6}\) 。
translated by @liangbowen 。
设操作次数为 \(x\) ,则总时间为 \(T(x) = \dfrac{A}{1+x} + Bx\) 。
根据初等函数求导法则对 \(T(x)\) 求导得:\(T^{\prime}(x) = B - \dfrac{A}{2(x+1)^{\frac{3}{2}}}\) 。
令 \(T^\prime(x) = 0 \Rightarrow x = (\dfrac{A}{2B})^{\frac{2}{3}} - 1\) 。
因为 \(x \in \mathbb{N+}\) ,所以 \(x = \text{round}((\dfrac{A}{2B})^{\frac{2}{3}} - 1)\) 。
注意到 \(A, B\) 上界为 \(10^{18}\) ,所以要拆开算。
得到 \(x\) 的值之后带入 \(T(x)\) 即可得到答案。
不过这种函数求最值的容易出误差,不然就二分,不然就在极值点附近多取几个点求 \(\min\) ,不然难顶。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33 // author : black_trees
#include <cmath> #include <cstdio> #include <cstring> #include <iomanip> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; using ldb = long double ; const ldb alpha = ( 1.0 / 3.0 ); int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); ldb a , b ; cin >> a >> b , b *= 2.0 ; ldb x = round ((( pow ( a , alpha ) * pow ( a , alpha )) / ( pow ( b , alpha ) * pow ( b , alpha ))) - 1.0 ); if ( x < 0 ) x = 0 ; ldb ans = 1e18 + 7 ; for ( ldb i = max (( ldb ) 0.0 , x - 10.0 ); i <= min (( ldb ) 1e18 + 7.0 , x + 10.0 ); i += 1.0 ) ans = min ( ans , ( b / 2.0 ) * i + ( a / sqrt ( i + 1.0 ))); cout << fixed << setprecision ( 10 ) << ans << endl ; return 0 ; }
ABC279E - Cheating Amidakuji
给你两个数组 \(A\) 和 \(B\) ,初始时,\(B_i=i\) 。
定义第 \(k\) 次操作为 \(\operatorname{swap}(B_{A_k},B_{A_k+1})\)
定义 \(S_i\) 为依次进行 \(1\) 到 \(m\) 除 \(i\) 号操作外的所有操作后,数字 \(1\) 在 \(B\) 数组中的位置。
请依次输出 \(S_i\) 。
注意到有些操作是不会影响 \(1\) 的位置的,我们只需要关心 \(1\) 的位置。
可以先记录直接进行所有操作之后每一个元素的位置 \(p\) 。
注意到 \(ans_i\) 是表示不进行操作 \(i\) 的情况,所以可以先做 \(1 \sim i\) ,然后看一下当前交换的两个元素 \(b(a(i)), b(a(i) + 1)\) 哪个是 \(1\) ,如果 \(b(a(i))\) 是 \(1\) ,答案就是 \(p(b(a(i) + 1))\) ,反之亦然,如果都不是 \(1\) 证明他们对答案没有影响,答案是 \(p(1)\) 。
复杂度 \(O(n)\) 。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 // author : black_trees
#include <cmath> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; const int si = 2e5 + 10 ; int n , m ; int a [ si ], b [ si ], p [ si ]; int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); cin >> n >> m ; for ( int i = 1 ; i <= m ; ++ i ) cin >> a [ i ]; for ( int i = 1 ; i <= n ; ++ i ) b [ i ] = i ; for ( int i = 1 ; i <= m ; ++ i ) swap ( b [ a [ i ]], b [ a [ i ] + 1 ]); for ( int i = 1 ; i <= n ; ++ i ) p [ b [ i ]] = i , b [ i ] = i ; for ( int i = 1 ; i <= m ; ++ i ) { if ( b [ a [ i ]] == 1 ) cout << p [ b [ a [ i ] + 1 ]] << endl ; else if ( b [ a [ i ] + 1 ] == 1 ) cout << p [ b [ a [ i ]]] << endl ; else cout << p [ 1 ] << endl ; swap ( b [ a [ i ]], b [ a [ i ] + 1 ]); } return 0 ; }
ABC279F - BOX
有 \(N\) 个箱子和无数个编号从 \(1\) 开始的球,第 \(i\) 个箱子开始时只装了编号为 \(i\) 的球。
有 \(Q\) 次操作,每次操作分别可能为:
1 X Y 将 \(Y\) 箱中的球全部放入 \(X\) 箱。2 X 将目前最小的未被放到箱子里的球放到 \(X\) 箱。3 X 查询 \(X\) 球在哪个箱子中,输出该箱编号,输出间用换行隔开。
首先这个 \(10^{100}\) 一看就是吓人的,注意到 \(n, q \le 3e5\) ,所以每个盒子里的球数肯定不超过 \(3e5\) ,并且盒子是不会新产生的,所以离散化也不需要。
但是注意到集合和小球各自是有编号的,所以我们还需要分开处理,这个就用一个 map 标记一下就行了(为什么不是 bool array 在下面能得到解释)。
首先看操作 \(1\) ,把一个盒子的球放到另外一个里面。
注意这不是简单的 Merge,而是 Merge 完了之后还要清空。
但是如果我们直接 Merge 过去,\(y\) 下面挂着那么多节点,而且也不能直接反向访问到,肯定会有问题。
这时候有一个新奇的想法,我们考虑给 \(y\) 建一个副本来代替 \(y\) 这个盒子的位置,然后直接把原来的 \(y\) Merge 到 \(x\) 里面,并且这个 \(y\) 自己本身不算 \(size\) ,那实现的时候就需要离散化了。
具体方式是,把原来的集合直接 Merge 过去,记录它不再是一个盒子,而是一个中转节点且不占 \(size\) ,然后把这个盒子的编号映射到一个新的副本上面,初始化这个副本的信息,并且不算 \(size\) 。
然后发现操作 \(2\) 本质是类似的,只不过我们现在是保留这个节点,新开一个副本 Add 到盒子里面去,且这个副本不算 \(size\) ,并把原来节点所在集合 \(size\) 减一。
操作 \(3\) 就是简单的询问。
完蛋,读错题了,我以为操作二是考虑当前盒子有多少个。
纯纯傻逼啊,但是感觉这个题可以出出来扔给普及组小朋友练习。
但是如果没有这个限制感觉也差不多。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120 // author : black_trees
#include <cmath> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; const int si = 3e5 + 10 ; int n , m , q ; int raw [ si << 2 ], val [ si << 2 ], pa [ si << 2 ], b [ si << 2 ]; int root ( int x ) {
if ( pa [ x ] != x ) return pa [ x ] = root ( pa [ x ]); return pa [ x ]; } int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); cin >> n >> q , m = n ; for ( int i = 1 ; i <= n ; ++ i ) pa [ i ] = raw [ i ] = val [ i ] = b [ i ] = i ; int tot = n ; for ( int i = 1 ; i <= q ; ++ i ) { int opt , x , y ; cin >> opt ; if ( opt == 3 ) cin >> x , cout << raw [ root ( b [ x ])] << endl ; if ( opt == 1 ) cin >> x >> y , pa [ val [ y ]] = pa [ val [ x ]], val [ y ] = ++ m , raw [ m ] = y , pa [ m ] = m ; if ( opt == 2 ) cin >> x , b [ ++ tot ] = val [ x ]; } return 0 ; } // ()()()(?
/* // author : black_trees
#include <map>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define endl '\n'
using namespace std;
using i64 = long long;
const int si = 3e5 + 10;
int n, m, q;
int raw[si << 2], val[si << 2];
std::map<int, bool> is_box;
int pa[si << 2], siz[si << 2];
int root(int x) {
if(pa[x] != x)
pa[x] = root(pa[x]);
return pa[x];
}
void Merge(int x, int y) {
int rx = root(x), ry = root(y);
if(rx == ry) return;
pa[ry] = rx, siz[rx] += siz[ry];
}
int main() {
cin.tie(0) -> sync_with_stdio(false);
cin.exceptions(cin.failbit | cin.badbit);
cin >> n >> q, m = n + n;
for(int i = 1; i <= n; ++i) {
raw[i] = i, pa[i] = i, siz[i] = 0;
is_box[i] = true;
} // init boxes
for(int i = 1; i <= n; ++i) {
raw[i + n] = i, val[i] = i + n, siz[i + n] = 0, pa[i + n] = i + n;
} // init balls;
for(int i = 1; i <= q; ++i) {
int opt, x, y;
cin >> opt;
if(opt == 3) cin >> x, cout << raw[root(x)] << endl;
if(opt == 1) {
cin >> x >> y;
++m, raw[m] = raw[y], siz[m] = 0, pa[m] = m; // new copy
is_box[m] = true, is_box[y] = false, Merge(x, y);
}
if(opt == 2) {
cin >> x;
int rx = root(x), sz = siz[rx];
if(sz >= n) {
++m, pa[m] = m, siz[m] = 1;
raw[m] = sz + 1, val[sz + 1] = m;
}
else {
int ry = root(sz + 1);
siz[ry]--, raw[val[sz + 1]] = -1;
++m, pa[m] = m, siz[m] = 1, raw[m] = sz + 1, val[sz + 1] = m;
Merge(rx, m);
}
}
}
return 0;
}
// ()()()(? */
ABC280D - Factorial and Multiple
给出一个数 \(k\) ,求一个数 \(n\) ,要求 \(n!\) 是 \(k\) 的倍数,输出 \(n\) 的最小值。
\(k\le10^{12}\)
translated by @PineappleSummer 。
没啥好说的,分解质因数然后求 \(\max\{p_i^{c_i}!\}\) 即可。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 // author : black_trees
#include <cmath> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; const int si = 1e6 + 10 ; i64 c [ si ]; // exponential
i64 m = 0 , p [ si ]; // prime factor
i64 ans = 1 ; void divide ( i64 n ) { m = 0 ; for ( i64 i = 2 ; i * i <= n ; ++ i ) { if ( n % i == 0 ) { p [ ++ m ] = i , c [ m ] = 0 ; while ( n % i == 0 ) n /= i , c [ m ] ++ ; i64 tmp = 0 , t ; while ( c [ m ] > 0 ) { tmp += i , t = tmp ; while ( t % i == 0 ) t /= i , c [ m ] -- ; } ans = max ( ans , tmp ); } } if ( n > 1 ) p [ ++ m ] = n , c [ m ] = 1 ; ans = max ( ans , n ); } int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); i64 k ; cin >> k ;
divide ( k ), cout << ans << endl ; return 0 ; }
ABC280E - Critical Hit
有一个 \(n\) 滴血的怪物。每一次攻击你有 \(P\%\) 的概率让它失去 \(2\) 滴血,有 \((100-P)\%\) 的概率让它失去 \(1\) 滴血。如果攻击过后怪物的血量 \(\leq 0\) ,它就死了。你需要一直攻击怪物直到它死亡。输出攻击次数的期望对 \(998244353\) 取模的值。
\(1\leq n\leq 2\times10^5,0\leq P\leq 100\)
就是简单的期望 dp,但是我一时半会没想清楚。
就是设 \(dp(i)\) 表示打死一只体力为 \(i\) 的怪物的期望步数。
因为 stamina = 1 的时候怎么打都是 G,所以 \(dp(1) = 1\) 。
方程比较显然,\(dp(i) = \dfrac{100 - p}{100}dp(i - 1) + \dfrac{p}{100}dp(i - 2) + 1\) 但是我搞不懂啊,你如果打出了 \(i + 1\) 的伤害,那 \(i\) 不是照样会 G 吗?
答案怎么就是 \(dp(n)\) 了,不懂,不懂。
感觉比较好理解的是倒推?
就设 \(dp(i)\) 表示把怪物打到恰好剩 \(i\) 的 stamina 的期望步数。
那么 \(dp(n) = 0\) ,答案是 \(dp(0) + dp(-1)\) ,然后求出 \(dp(1)\) 之后显然不管怎么打都是可以的。
所以答案实际上是 \(dp(1) + 1\) 。
哦,我懂了,上面的状态是打死,下面的是恰好,有区别的。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43 // author : black_trees
#include <cmath> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; // using i64 = long long;
#define int long long
const int si = 2e5 + 10 ; const int mod = 998244353 ; int n , p ; int dp [ si ]; int qpow ( int a , int b ) { int ret = 1 % mod ; for (; b ; b >>= 1 ) { if ( b & 1 ) ret = ret * a % mod ; a = a * a % mod ; } return ret % mod ; } int inv ( int x ) { return qpow ( x , mod - 2 ); } const int iv = inv ( 100 ); signed main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); cin >> n >> p ; dp [ 0 ] = 0 , dp [ 1 ] = 1 ;
for ( int i = 2 ; i <= n + 1 ; ++ i ) dp [ i ] = (( dp [ i - 1 ] * ( 100 - p + mod ) % mod * iv % mod ) + ( dp [ i - 2 ] * p % mod * iv % mod ) + 1 % mod + mod ) % mod ; cout << dp [ n ] << endl ; return 0 ; }
代码是第一个定义。
ABC280F - Pay or Receive
有 \(n\) 个小镇,编号 \(1\) ~ \(n\) ,还有 \(m\) 条路,编号 \(1\) ~ \(m\) 。
第 \(i\) 条路连接 \({A_i}\) 和 \({B_i}\) ,当你走过一条路时,你的得分 会遵循以下变化:
当你用第 \(i\) 条路从 \({A_i}\) 到 \({B_i}\) ,你的得分增加 \({C_i}\) ; 当你用第 \(i\) 条路从 \({B_i}\) 到 \({A_i}\) ,你的得分减少 \({C_i}\) 。
你的得分可能为负数。
回答如下的 \(Q\) 个问题:
如果你从 \({X_i}\) 这个小镇出发(初始得分为 \(0\) ), 求出你在 \({Y_i}\) 小镇时的最大得分。
如果你不能从 \({X_i}\) 这个小镇出发到达 \({Y_i}\) 小镇,输出 nan 。
如果你从 \({X_i}\) 这个小镇出发到达 \({Y_i}\) 小镇可以挣得无限的分数,输出 inf 。
这不就正反建边最长路判下可达性判下正环?
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94 // author : black_trees
#include <cmath> #include <queue> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
#define int long long
using namespace std ; using i64 = long long ; const int inf = -1e18 ; const int si_n = 1e5 + 10 ; const int si_m = 2e5 + 10 ; int n , m , Q ; int tot = 0 , head [ si_n ]; bool vis [ si_n ], ring [ si_n ]; int pa [ si_n ], cnt [ si_n ], dis [ si_n ]; struct Edge { int ver , Next , w ; } e [ si_m ]; inline void add ( int u , int v , int w ) { e [ tot ] = ( Edge ){ v , head [ u ], w }, head [ u ] = tot ++ ; } int root ( int x ) { if ( pa [ x ] != x ) pa [ x ] = root ( pa [ x ]); return pa [ x ]; } void Merge ( int u , int v ) { int ru = root ( u ), rv = root ( v ); if ( ru == rv ) return ; pa [ ru ] = rv ; return ; } std :: queue < int > q ; void bfs ( int st ) { q . push ( st ), vis [ st ] = true , dis [ st ] = 0 ; while ( ! q . empty ()) { auto u = q . front (); q . pop (); for ( int i = head [ u ]; ~ i ; i = e [ i ]. Next ) { int v = e [ i ]. ver ; if ( dis [ v ] == inf ) { dis [ v ] = dis [ u ] + e [ i ]. w ; vis [ v ] = true ; q . push ( v ); } else if ( dis [ v ] != dis [ u ] + e [ i ]. w ) { ring [ root ( st )] = true ; return ; } } } } signed main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); memset ( head , -1 , sizeof head ); cin >> n >> m >> Q ; for ( int i = 1 ; i <= n ; ++ i )
pa [ i ] = i , dis [ i ] = inf ; for ( int i = 1 ; i <= m ; ++ i ) { int u , v , w ; cin >> u >> v >> w ; add ( u , v , w ), add ( v , u , - w ); if ( root ( u ) != root ( v )) Merge ( u , v ); } for ( int i = 1 ; i <= n ; ++ i ) { int j = root ( i ); if ( vis [ j ]) continue ; while ( ! q . empty ()) q . pop (); vis [ j ] = true , bfs ( j ); } for ( int i = 1 ; i <= Q ; ++ i ) { int u , v ; cin >> u >> v ; if ( root ( u ) != root ( v )) { cout << "nan" << endl ; continue ; } if ( ring [ root ( u )]) cout << "inf" << endl ; else cout << dis [ v ] - dis [ u ] << endl ; } return 0 ; } // ()()()(?
// https://www.cnblogs.com/CTing/p/16950621.html
ABC281D - Max Multiple
给定 \(n\) 个数。现在可以从中选 \(k\) 个数,需满足他们的和为 \(d\) 的倍数。求最大和值。
translated by @liangbowen 。
太蠢了,怎么稍微一久甚至连这种神必背包都不会。
怎么回事呢。
就是看到这个从一堆元素里任意选 \(K\) 个要满足一定的条件,问某些权值的最值或者是可行的方案数。
然后就是背包嘛,然后数据范围都是 \(100\) ,很容易想到设 \(dp(i,j,k)\) 表示考虑前 \(i\) 个元素选了 \(j\) 个,且已经选择的元素的模 \(D\) 意义下和为 \(k\) 的时候的 \(\max\sum\) 。
终态 \(dp(N, K, 0)\) 。
转移比较简单就选或者不选,\(O(NKD)\) 。
只能说越来越傻逼了,状态不初始化 inf 初始化 -1 根本不够,然后转移的时候乱转移状态,同一层转移两个不同状态,纯纯nt.
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 // author : black_trees
#include <cmath> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; const int si = 1e2 + 10 ; int N , K , D , a [ si ]; i64 dp [ si ][ si ][ si ]; int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); cin >> N >> K >> D ; for ( int i = 1 ; i <= N ; ++ i ) cin >> a [ i ]; memset ( dp , -0x3f , sizeof dp ); dp [ 1 ][ 0 ][ 0 ] = 0 , dp [ 1 ][ 1 ][( a [ 1 ] % D )] = a [ 1 ]; for ( int i = 2 ; i <= N ; ++ i ) { for ( int j = 0 ; j <= min ( i , K ); ++ j ) { for ( int k = 0 ; k < D ; ++ k ) { dp [ i ][ j ][ k ] = max ( dp [ i ][ j ][ k ], dp [ i - 1 ][ j ][ k ]); if ( j > 0 ) dp [ i ][ j ][ k ] = max ( dp [ i ][ j ][ k ], dp [ i - 1 ][ j - 1 ][(( k - a [ i ]) % D + D ) % D ] + a [ i ]); } } } cout << (( dp [ N ][ K ][ 0 ] < 0 ) ? -1 : dp [ N ][ K ][ 0 ]) << endl ; return 0 ; }
ABC281E - Least Elements
给定一个序列 \(A\) ,对于每个 \(1 \le i \le N - M + 1\) ,将 \(A_i A_{i + 1} \cdots A_{i + M - 1}\) 从小到大 排序后(不影响原序列),求出 \(\mathrm{ans}_i = \sum\limits_{i=1}^{K}A_i\) 。
感觉这种对于一个序列做很多个 independent problem 的时候一般都会要考虑从上一个状态继承,或者是考虑先整体做一遍再计算 ignore 一些操作之后的影响之类的。
这一题是,279E 也是,其实很经典感觉,之前好像有一个 CF 的题也是类似,有点久远记不清楚了。
就是先考虑对于 \(i = 1\) 直接暴力做一次,然后我们发现每次挪一步就少一个多一个元素而已,所以我们只需要动态维护前 \(k\) 大的 \(\sum\) 就可以,每次弹出一个元素,然后加入一个新元素看有没有变化。
这个过程可以直接 multiset 维护,思想和莫队很像,但是边界好TM烦啊,不是很懂啊,好像要两个 multiset 维护,我一个 multiset 假了,不是很懂。
两个 multiset 维护过程就类似对顶堆,只需要判下 size 就行了,可以少分讨一点。
Code
// 上面的代码假了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148 // author : black_trees
#include <set> #include <cmath> #include <cstdio> #include <cstring> #include <cassert> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; const int si = 2e5 + 10 ; int N , M , K , a [ si ], b [ si ]; class SuzuiAnri { private : i64 sum ; int kth ; std :: multiset < int > ms ; public : void Init () { for ( int i = 1 ; i <= M ; ++ i ) b [ i ] = a [ i ]; sort ( b + 1 , b + 1 + M ); for ( int i = 1 ; i <= K ; ++ i ) sum += b [ i ]; for ( int i = 1 ; i <= M ; ++ i ) ms . insert ( a [ i ]); kth = b [ K ]; } i64 Qsum () { return sum ; } void Do ( int i ) { int x = a [ i - 1 ], y = a [ i + M - 1 ]; if ( K != M ) { if ( x > kth ) ms . erase ( ms . find ( x )); else { ms . erase ( ms . find ( x )); kth = * next ( ms . find ( kth )); sum -= x , sum += kth ; } if ( y > kth ) ms . insert ( y ); else { ms . insert ( y ); sum += y , sum -= kth ; kth = * prev ( ms . find ( kth )); } }
else sum -= x , sum += y ;
} } DD ; int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); cin >> N >> M >> K ; for ( int i = 1 ; i <= N ; ++ i ) cin >> a [ i ]; DD . Init (); cout << DD . Qsum () << endl ;
for ( int i = 2 ; i <= N - M + 1 ; ++ i ) DD . Do ( i ), cout << DD . Qsum () << " " ; cout << endl ; return 0 ; } /* 先不考虑 K = M
* 如果新加入的为 y, 要被删除的为 x
* 首先考虑 x 的位置:
* 如果 x 不属于前 k 小:
* 直接删除 x,不会有任何影响。
* 如果 x 属于前 k 小:
* 删除 x,然后 kth 应该更新为原来 kth 的后一个元素,因为 K < M 所以一定会有这样的一个元素,不会越界。
* 然后考虑 y 的位置:
* 如果 y 不属于前 k 小:
* 直接插入 y,不会有任何影响。
* 如果 y 属于前 k 小:
* 直接插入 y,然后更新 kth 为现在的前一位,如果 K = 1,因为 y 属于前 K 小所以一定存在,其它也一定存在,不会越界。
* 然后 K = M 直接输出就行了。
*/ /*
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using namespace std;
using ll = long long;
struct DS {
int k;
ll sum;
multiset<int> ls, rs;
DS(int k=0): k(k), sum(0) {}
void ladd(int x) {
sum += x;
ls.insert(x);
}
void lerase(multiset<int>::iterator it) {
sum -= *it;
ls.erase(it);
}
void add(int x) {
ladd(x);
if (ls.size() <= k) return;
auto it = ls.end(); --it;
rs.insert(*it);
lerase(it);
}
void erase(int x) {
if (*ls.rbegin() < x) {
rs.erase(rs.find(x));
}
else {
lerase(ls.find(x));
auto it = rs.begin();
ladd(*it);
rs.erase(it);
}
}
};
int main() {
int n, m, k;
cin >> n >> m >> k;
vector<int> a(n);
rep(i, n) cin >> a[i];
DS d(k);
rep(i, m) d.add(a[i]);
cout << d.sum << '\n';
rep(i, n-m) {
d.add(a[i+m]);
d.erase(a[i]);
cout << d.sum << '\n';
}
return 0;
}
作者:Ncik
链接:https://www.acwing.com/solution/content/154338/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
*/
ABC281F - Xor Minimization
求 \(\min\{\max\{a_i \oplus x\}\}\) ,其中 \(x\) 未知。
\(a_i < 2^{30}, 1\le n \le 2e5\) 。
首先观察内层的 \(\max\) ,发现这个就是 01trie 的 query 操作。
那么问题就是怎么样让 01trie 的 query 找到的值最小。
思考一下 query 的过程,实际上就是不断反着走,我们希望它尽量小,那就是让它的高位尽量不能反着走,也就是尽量在高位找只有一个指针的边。
但是我们不能很好的知道下面的情况,比如你同一层两边都能走一个指针,但是下面能走的数量不同怎么办?
所以我们记录两个信息,一个 \(near(u)\) 表示除了 \(u\) 自己,能走到的最近的有一个分叉的点的位置,另一个 \(cnt(u)\) 表示 \(u\) 这个节点下面有多少层能有一个指针的选择,然后 cnt 需要反过来决定 near。
但是这样非常麻烦,我们思考一下能不能直接在 \(u\) 就确定。
考虑所有数的第 \(i\) 位,如果全部是 \(0/1\) ,那么 \(x\) 的第 \(i\) 位一定是 \(1/0\) 。
如果有 \(0\) 有 \(1\) ,显然 \(x\) 的这一位需要由低位的结果确定,而且这一位的结果一定是 1,所以我们选择低位答案更小的即可。
所以我们就分治下去算一下答案,然后不断向上 merge 即可,这个过程可以在 01trie 上做。
感觉这个模型也比较经典,就是对于之后的信息可能造成影响时的处理方式,不是递归下去直接预处理信息,就是先分治然后倒着算答案。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55 // author : black_trees
#include <cmath> #include <cstdio> #include <climits> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; const int si = 2e5 + 10 ; const int inf = INT_MAX ; int tot = 1 ; bool tg [ si * 31 ]; int tr [ si * 31 ][ 2 ], val [ si * 31 ]; void insert ( int v ) { int p = 1 ; for ( int i = 30 ; i >= 0 ; -- i ) { int ch = ( v >> i ) & 1 ; val [ p ] = 1 << i ; if ( ! tr [ p ][ ch ])
tr [ p ][ ch ] = ++ tot ; p = tr [ p ][ ch ];
} tg [ p ] = true ; } int query ( int p ) { if ( tg [ p ]) return 0 ; if ( ! p ) return - inf ; int lans = query ( tr [ p ][ 0 ]), rans = query ( tr [ p ][ 1 ]); if ( lans > rans ) swap ( lans , rans ); return max ( val [ p ] + lans , rans ); } int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); int n , rt = 1 ; cin >> n ; for ( int i = 1 ; i <= n ; ++ i ) { int x ; cin >> x ; insert ( x ); } cout << query ( 1 ) << endl ; return 0 ; } // ()()()(?
说句鲜花,发现早上的时候确实清醒很多,感觉以后不能浪费早上的时间了。
CF35E 全是早上挑出重大 bug,今天上午做题效率很高。
哦还有感觉以后做题之前可以先翻一下以前的博客找找?状态?
CF1770 - Goodbye2022
感觉是今年打的最好的一场。
从各种意义上来说都是,感觉自己能尝试一下 D 这种披着博弈论皮的题已经算进步了,以前看到 both play optimally 就不敢做(
回来的地铁上和一个特别厉害的前 MOer 聊天,他说他做题一般是要先想方法,没有确切思路绝对不开始写,不然就先尝试简化题目然后继续思考。
而且一般来说要尝试分析考点然后找到方向,使劲往那个方向靠。
而且一般来说不能有 phobia,得先思考一下,别被吓到了。
感觉很有道理!说的太对了!
虽然别人的方法不一定适合,但是感觉这个确实会比较有用!
A - Koxia and Whiteboards
没什么好说的。
B - Koxia and Permutation
你需要构造一个排列 \(p\) ,使得 \(\max\limits_{i = 1}^{n - k + 1}\{\max(a_i \dots a_{i + k - 1}) + \min(a_i \dots a_{i + k - 1})\}\) 最小。
\(n, k\) 给定,\(2e5\) 。
注意到我们一定希望整体的 \(\max,\min\) 凑到一起,我们把他们放到一个区间之后去掉他们,然后可以递归的发现就是不断让 \(\max \min\) 放到一起。
然后瞎构造一下就可以了,我开始的思路是直接放区间左右端点,但是感觉比较麻烦,然后发现其实答案和 \(k\) 无关,直接 \(\max \min\) 这样挨着放就行了。
赛时Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 // author : black_trees
#include <cmath> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; const int si = 2e5 + 10 ; int a [ si ]; int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); int T ; cin >> T ; while ( T -- ) { int n , k ; cin >> n >> k ; for ( int i = 1 ; i <= n ; ++ i ) { if ( i & 1 ) cout << ( n - i / 2 ) << " " ; else cout << ( i >> 1 ) << " " ; } // int l = 1, r = n;
// int pos = 1;
// while(l <= r) {
//
// }
// for(int i = 1; i <= n; ++i) cout << a[i] << " ", a[i] = 0;
cout << endl ; } return 0 ; }
C - Koxia and Number Theory
给定一个序列 \(a\) , 判断是否存在一个正整数 \(x\) 使得 \(\forall 1 \le i < j \le n, \gcd(a_i + x, a_j + x) = 1\) 。
\(1\le n \le 2e5, 1\le a_i 1e18\)
问题等价于判断是否存在一个 \(x\) 使得每一个值域内的质数都至多整除一个 \(a_i + x\) 。
但是值域是 \(10^{18}\) ,思考一下能否缩小范围。
发现对于一个质数 \(p\) ,显然我们要做的是对 \(a_i \mod p\) 意义下的余数计数,所以其实对于当前枚举到的 \(p\) ,如果它大于 \(n\) ,显然一定存在至少一个余数的出现次数数是一定会大于 \(2\) 的,所以寄。
那么就枚举 \([2,n]\) 范围内的质数就行了,发现其实合数对答案没影响,所以质数都不需要判了。
记得判相等的 \(a_i, a_j\) 。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49 // author : black_trees
#include <cmath> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; const int si = 2e5 + 10 ; i64 a [ si ], b [ si ]; int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); int T ; cin >> T ; while ( T -- ) { bool f = false ; int n ; cin >> n ; for ( int i = 1 ; i <= n ; ++ i ) cin >> a [ i ]; for ( int i = 1 ; i <= n ; ++ i ) { for ( int j = i + 1 ; j <= n ; ++ j ) { if ( a [ i ] == a [ j ]) { f = true ; break ; } } if ( f ) break ; } if ( f ) { cout << "No" << endl ; continue ; } for ( int p = 2 ; p <= n ; ++ p ) { for ( int i = 0 ; i <= p ; ++ i ) b [ i ] = 0 ; for ( int i = 1 ; i <= n ; ++ i ) b [ a [ i ] % p ] += 1 ; bool ff = false ; for ( int i = 0 ; i < p ; ++ i ) if ( b [ i ] <= 1 ) { ff = true ; break ; }
if ( ff != true ) { f = true ; break ; } } if ( f ) cout << "No" << endl ; else cout << "Yes" << endl ; } return 0 ; }
D - Koxia and Game
给定两个序列 \(a, b\) ,要求构造一个序列 \(c\) 使得以下游戏先手必胜。
在游戏的第 \(i\) 轮,先手从 \(a_i, b_i, c_i\) 当中选取一个数删掉,然后后手在剩下的两个数里面选择一个,这次决策选择的数记为 \(d_i\) 。
如果 \(d\) 是一个 \(1\sim n\) 的排列,那么先手获胜,双方均采取最优策略。
请问有多少种合法的构造方案?对 \(998244353\) 取模。
\(1\le n \le 1e5\) 。
注意到这里是合法方案计数,所以显然我们需要知道什么样的方案是合法的。
观察样例发现会有无解的情况,发现不是很好判定,先考虑有解怎么算。
赛时这个时候突然冒出来一个思路,比较神奇,也不知道怎么想到的,可能是想尝试分析这个最优策略是什么的时候想到的。
就是发现其实这个游戏是由先手操纵的,和后手并没有任何关系。
因为只给出了 \(a_i, b_i\) ,所以其实先手可以强制后手选择 \(a_i\ \text{or}\ b_i\) ,具体方式是令 \(c_i\) 和需要强制后手选的那个数一样,然后删掉另外一个不同的即可。
考虑一下这个是不是最优策略,发现一定是,比如 1 1 2,你肯定不希望后手能有更多选择,不然你没法考虑后面的情况,比较容易寄掉,于是合理推测只能这么干!
然后考虑怎么算贡献,发现这个东西好像可以抽象成图论,就直接对于 \(i\) ,连 \((a_i, b_i)\) 这条无向边就行。
如果找到了一个自环,这里的贡献显然是 \(n\) ,因为 \(c_i\) 取任意一个数,先手都可以删掉,就比如 1 1 这样。
然后注意到其实合法方案应该是一个基环树森林,如果环不是自环,那么贡献一定是 \(2\) ,因为你每次之有两种选择,然后连通块里面的方案是会相互影响的,你好比选了两条路走出去这样。
那么其实自环的贡献应该在它所属的联通块里面直接算,所以我们直接 dfs 一下,判一下自环和无解就行了。
无解显然就是连通块不是基环树,也就是树的情况,那么就很好做了。
当然也有可能是凑不出排列,这个特判 vis 就行。
这里放的是赛时代码,错误思路的东西没来得及删,凑合着看。
这题也比较有纪念意义感觉,毕竟是 15 岁的我做的最后一题,16 岁的我做的第一题。
点名批评 15 岁的我,怎么判重复二元组这种假做法都能想到
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76 // author : black_trees
#include <map> #include <cmath> #include <cstdio> #include <cstring> #include <utility> #include <iostream> #include <algorithm> #define endl '\n'
#define int long long
using namespace std ; using i64 = long long ; const int si = 2e5 + 10 ; const int mod = 998244353 ; int a [ si ], b [ si ]; std :: map < std :: pair < int , int > , bool > mp ; bool vis [ si ]; int head [ si ], tot = 0 ; struct Edge { int ver , Next ; } e [ si << 1 ]; inline void add ( int u , int v ) { e [ tot ] = ( Edge ){ v , head [ u ]}, head [ u ] = tot ++ ; }
int dg , sf , deg [ si ]; void dfs ( int u , int fa ) { vis [ u ] = true ; dg -= 2 ; for ( int i = head [ u ]; ~ i ; i = e [ i ]. Next ) { int v = e [ i ]. ver ; dg ++ ; if ( u == v ) sf ++ ; // self ring.
if ( v == fa || vis [ v ] == true ) continue ; dfs ( v , u ); }
} signed main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); int T ; cin >> T ; while ( T -- ) { bool f = false ; mp . clear (), tot = 0 ; int n , ans = 1l l ; cin >> n ; for ( int i = 0 ; i <= n + 10 ; ++ i ) vis [ i ] = false , head [ i ] = -1 , deg [ i ] = 0 ; for ( int i = 1 ; i <= n ; ++ i ) cin >> a [ i ]; for ( int i = 1 ; i <= n ; ++ i ) cin >> b [ i ]; // for(int i = 1; i <= n; ++i) {
// std::pair<int, int> t = make_pair(min(a[i], b[i]), max(a[i], b[i]));
// if(mp[t] == true) { f = true; break; }
// mp[t] = true;
// if(a[i] == b[i]) ans = (ans * n) % mod, vis[i] = true;
// else add(a[i], b[i]), add(b[i], a[i]);
// }
for ( int i = 1 ; i <= n ; ++ i ) deg [ a [ i ]] ++ , deg [ b [ i ]] ++ , add ( a [ i ], b [ i ]), add ( b [ i ], a [ i ]); // if(f) { cout << "0" << endl; continue; }
for ( int i = 1 ; i <= n ; ++ i ) { if ( ! vis [ i ]) { dg = 0 , sf = 0 , dfs ( i , 0 ); if ( dg != 0 ) { ans = 0 ; break ; } if ( sf ) ans = ( ans * n ) % mod ; else ans = ( ans + ans ) % mod ;
} } for ( int i = 1 ; i <= n ; ++ i ) { if ( ! deg [ i ]) { ans = 0 ; break ; } } cout << ans << endl ; } return 0 ; } // dottle : 364577
ABC282D - Make Bipartite 2
给定一个 \(N\) 个点,\(M\) 条边的无向图,求问有多少对还未经连接的点对满足在连接它们后,该图为一个二分图.
注意这里点对 \((u,v)\) 和点对 \((v,u)\) 是同一对点对。
数据保证没有自环与重边。
首先考虑直接对 \(G\) 黑白染色判断一下有没有合法的解。
然后发现其实可以枚举白色点,check 一下能和他匹配的黑点有多少(就是黑点总数减去当前点的度数)。
但是注意到 \(G\) 可能是几个单独的联通分量,所以我们还要考虑分量外的方案。注意到对于当前点,如果是和外面的连通分量连,怎么连都行。
但直接这么干会算重,原因显然,要处理的话会比较复杂。
这样是正着算,非常麻烦。
所以我们考虑倒着算,也算是一种比较重要的想法来避免大分讨。
我们假设 \(G\) 是完全图,也就是把缺的边都连上,我们只需要计算有多少边是在同一个联通分量里面连接了同一种颜色的边即可。
设有 \(q\) 个连通块,第 \(i\) 个连通块有黑点 \(a_i\) 个,白点 \(b_i\) 个。
记 \(f(x) = x^2 - x\) ,那么答案就是 \(f(n) - m - \sum\limits_{i = 1}^q [f(a_i) + f(b_i)]\) 。
算是很基础的正难则反了。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66 // author : black_trees
#include <cmath> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; const int si = 2e5 + 10 ; int n , m ; int tot = 0 , head [ si ]; struct Edge { int ver , Next ; } e [ si << 1 ]; inline void add ( int u , int v ) { e [ tot ] = ( Edge ){ v , head [ u ]}, head [ u ] = tot ++ ; } int c [ si ], ok = 0 ; int cnt , a [ si ], b [ si ]; void dfs ( int u , int col ) { c [ u ] = col ; if ( col == 1 ) a [ cnt ] ++ ; else b [ cnt ] ++ ; for ( int i = head [ u ]; ~ i ; i = e [ i ]. Next ) { int v = e [ i ]. ver ; if ( c [ v ] == col ) { ok = -1 ; return ; } if ( c [ v ] == 3 - col ) continue ; if ( c [ v ] == 0 ) dfs ( v , 3 - col ); } return ; } int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); memset ( c , 0 , sizeof c ); memset ( head , -1 , sizeof head ); cin >> n >> m ; for ( int i = 1 ; i <= m ; ++ i ) { int u , v ; cin >> u >> v ; add ( u , v ), add ( v , u ); } i64 ans = ( 1l l * n * ( n - 1 )) / 2l l - m ; for ( int i = 1 ; i <= n ; ++ i ) { if ( ! c [ i ]) { ++ cnt , dfs ( i , 1 ); if ( ok == -1 ) { cout << "0" << endl ; return 0 ; } ans -= ( 1l l * a [ cnt ] * ( a [ cnt ] - 1 )) / 2l l ; ans -= ( 1l l * b [ cnt ] * ( b [ cnt ] - 1 )) / 2l l ; }
} cout << ans << endl ; return 0 ; } // ()()()(?
ABC282E - Choose Two and Eat One
题面暂略
怎么就是最大生成树啊卧槽。
就是 \((x, y)\) 连一条 \(x^y + y^x (\mod m)\) 的边,然后最大生成树就行了。
感觉要想到这个应该需要注意到选 n - 1 个吧。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73 // author : black_trees
#include <cmath> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; #define int i64
const int si = 5e2 + 10 ; int n , m ; int a [ si ]; int qpow ( int v , int b , int mod ) { int ret = 1 % mod ; for (; b ; b >>= 1 ) { if ( b & 1 ) ret = ( ret * v % mod ) % mod ; v = ( v * v % mod ) % mod ;
} return ret % mod ; } struct Edge { int x , y , w ; bool operator < ( const Edge & b ) const { return w > b . w ; } } e [ si * si ]; int pa [ si ], cnt = 0 ; inline int root ( int x ) { if ( pa [ x ] != x ) pa [ x ] = root ( pa [ x ]); return pa [ x ]; } void Merge ( int u , int v ) { int ru = root ( u ), rv = root ( v ); if ( ru == rv ) return ; pa [ ru ] = rv ; return ; } signed main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); cin >> n >> m ; for ( int i = 1 ; i <= n ; ++ i ) { cin >> a [ i ], pa [ i ] = i ; } for ( int i = 1 ; i <= n ; ++ i ) { for ( int j = i + 1 ; j <= n ; ++ j ) { e [ ++ cnt ] = ( Edge ){ i , j , ( qpow ( a [ i ], a [ j ], m ) + qpow ( a [ j ], a [ i ], m )) % m }; } } int ans = 0 ; sort ( e + 1 , e + 1 + cnt ); for ( int i = 1 ; i <= cnt ; ++ i ) { int u = e [ i ]. x , v = e [ i ]. y ; if ( root ( u ) == root ( v )) continue ; ans = ( ans + e [ i ]. w ), Merge ( u , v ); } cout << ans << endl ; return 0 ; } // ()()()(?
ABC282F - Union of Two Sets
这是一道交互题
首先,给出一个正整数 \(n\) (\(1\le n\le 4000\) ),你需要构造 \(m\) (\(1\le m\le 50000\) ) 个区间 \([l_i,r_i]\) ,满足 \(1\le l_i \le r_i \le n\) ,输出 \(m\) 和这 \(m\) 个区间,这些区间的编号按输出顺序依次为 \(1,2,\cdots ,m\) 。
然后,给出一个正整数 \(q\) (\(1\le q\le 10^5\) ),表示有 \(q\) 次询问。对于每次询问,给定区间 \([l,r]\) ,你要找到两个整数 \(i,j\) (\(1\le i,j \le n\) ,\(i\) 可以等于 \(j\) ),满足在第一步中构造的区间中 \([l_i,r_i]\) 与 \([l_j,r_j]\) 的并集等于 \([l,r]\) ,输出 \([i,j]\) 。
交互题,感觉就是什么神仙构造。
按尿性来看,交互题一般会限制构造或者操作的次数,所以观察数据范围是一个很好的选择。
显然 \(m\) 是越大越好,我们直接当作 \(5\times 10^4\) 处理。
然后发现 \(n\) 是 \(4\times 10^3\) ,我们希望是能凑出所有区间,所以不妨考虑枚举 \(i \in [1,n]\) 然后给每个 \(i\) 平均分配一下。
发现每个 \(i\) 能分到 \(m / n = 12.5\) 个区间,一般来说交互题会带 \(\log, 2^n\) 这样的形式,于是我们看 \(2^{12.5}\) 大概是多少,\(2^{12}\) 是 \(4096 > 4\times 10^3\) ,所以我们不难猜到可能是倍增的形式。
于是给每个 \(i\) 分配长度为 \(2^j, j \in [0, n)\) 的区间,每次询问的时候想办法凑就行了?
这样能凑出完整的区间吗?直觉上是可以的,因为有那个分解成 \(2\) 的次幂的结论。先试一试。
确实是这样的,这东西是 st 表啊。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60 // author : black_trees
#include <map> #include <cmath> #include <cstdio> #include <vector> #include <cassert> #include <cstring> #include <utility> #include <iostream> #include <algorithm> // #define endl '\n'
// interactive problem, use endl to flush the buffer.
using namespace std ; using i64 = long long ; const int si = 4e3 + 10 ; int n , m , q ; std :: vector < int > l [ si ], r [ si ]; std :: map < std :: pair < int , int > , int > mp ; int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); mp . clear (); cin >> n ; int t = ( int )( log ( n ) / log ( 2 )) + 1 ; for ( int i = 1 ; i <= n ; ++ i ) { for ( int j = 0 ; j <= t ; ++ j ) { // ? is this upperbound right?
if ( i + ( 1 << j ) - 1 > n ) continue ; ++ m , mp [ make_pair ( i , i + ( 1 << j ) - 1 )] = m ;
r [ i ]. push_back ( i + ( 1 << j ) - 1 ); l [ i + ( 1 << j ) - 1 ]. push_back ( i ); } } cout << m << endl ; for ( int i = 1 ; i <= n ; ++ i ) { for ( auto j : r [ i ]) cout << i << " " << j << endl ; } cin >> q ; while ( q -- ) { int L , R ; cin >> L >> R ; int a , b ; auto it = -- upper_bound ( r [ L ]. begin (), r [ L ]. end (), R ); auto itt = lower_bound ( l [ R ]. begin (), l [ R ]. end (), L ); a = mp [ make_pair ( L , * it )], b = mp [ make_pair ( * itt , R )]; cout << a << " " << b << endl , assert ( min ( L , * itt ) == L && max ( R , * it ) == R ); } return 0 ; } // ()()()(?
ABC283D - Scope
假设有一个字符串,只包含 (,)和小写字母。如果通过以下步骤,能使字符串为空,则称这个字符串为好的:
给定一个好的字符串 \(S\) 。字符串中所有的小写字母对应一个小球。此外,我们有一个箱子。
一个人按照 \(1,2,3,\cdots,|S|\) 的顺序取球:
如果 \(S_i\) 为(,什么也不做。
如果 \(S_i\) 为小写字母,就将这个小球放入箱子中。如果这个小球已经出现在箱子中,他会晕倒。
如果 \(S_i\) 为),取小于 \(i\) 的最大的 \(j\) ,使 \(S_i \sim S_j\) 这个子串是好的。将 \(j\) 到 \(i\) 操作中放入的小球全部取出。
这不就巨大蠢一个题,显然只能最近的左右括号配对,记录一下、模拟没了。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50 // author : black_trees
#include <cmath> #include <stack> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; const int si = 3e5 + 10 ; int cnt [ si ][ 31 ]; void solve () { string s ;
cin >> s , s = ' ' + s ; int n = s . size () - 1 ; std :: stack < int > stk ; for ( int i = 1 ; i <= n ; i ++ ) { for ( int j = 0 ; j < 26 ; j ++ ) cnt [ i ][ j ] = cnt [ i - 1 ][ j ]; if ( s [ i ] == '(' ) stk . push ( i ); else if ( s [ i ] == ')' ) { for ( int j = 0 ; j < 26 ; j ++ )
cnt [ i ][ j ] = cnt [ stk . top ()][ j ]; stk . pop (); } else { if ( cnt [ i ][ s [ i ] - 'a' ] >= 1 ) {
cout << "No" << endl ; return ; } cnt [ i ][ s [ i ] - 'a' ] ++ ; } } cout << "Yes" << endl ; } int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); solve (); return 0 ; } // ()()()(?
ABC283E - Don't Isolate Elements
给定一个 \(n\times m\) 的 \(01\) 矩阵 \(a\) ,称位于第 \(i\) 行第 \(j\) 列的元素为 \(a_{i,j}\) 。
你可以进行如下的操作任意次(可以是 \(0\) 次):
- 选择任意一行,翻转此行内的所有元素。
我们称 \(a_{i,j}\) 被隔离,当且仅当与其四联通的四个元素 \(a_{i - 1,j}, a_{i + 1, j}, a_{i, j - 1}, a_{i, j + 1}\) 的 \(01\) 性与其均不相同。
请输出使得给定矩阵中没有元素被隔离所需要的最小操作次数。如果无论如何操作都无法满足要求则输出 -1。
\(2\le n, m \le 1000\) 。
上次看到这种题是一个关灯的题,就是 0 1 0 -> 1 0 1 的这种,问到达合法状态最小步数,好像是个 bfs。
最大的问题是我不是很能找到这里面的一个“枚举顺序”,所以经常想不出来。
注意到一个事情是,没有孤立元素等价于没有大小为 \(1\) 的联通块,考虑一下怎么形式化这个操作。
有没有可能是先建图,然后建反图?之前见过这种状态很多,但是可以利用类似分层图的思想转化的题。
感觉比较类似,因为同层之间的边不是变化的,每次取反元素会让上下两层和当前层的边取反,并且显而易见的,每个行最多操作一次。
所以考虑直接枚举每一行然后考虑是否操作,因为会影响某一行的孤立元素的只有上下两行,相当于找到了一个枚举顺序。这个状态数能减到很小,应该是这样的。
注意到是上下两行,然后就感觉这种问题就不是很能贪心,就是不能直接扫一遍算,于是 dp,对于当前行和上一行加一个是否操作过的状态即可。
转移可能很麻烦,要判边界什么的。
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61 // author : black_trees
#include <cmath> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; const int si = 1e3 + 10 ; const int inf = 0x3f3f3f3f ; int n , m ; int a [ 2 ][ si ][ si ], dp [ si ][ 2 ][ 2 ]; bool check ( int l , int r , int u , int d , int mid ) { return ( l != mid && r != mid && u != mid && d != mid ); } int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); cin >> n >> m ; memset ( dp , 0x3f , sizeof dp ); for ( int i = 1 ; i <= n ; i ++ ) { for ( int j = 1 ; j <= m ; j ++ ) { cin >> a [ 0 ][ i ][ j ], a [ 1 ][ i ][ j ] = a [ 0 ][ i ][ j ] ^ 1 ; } } for ( int i = 0 ; i <= m + 1 ; i ++ ) a [ 0 ][ 0 ][ i ] = a [ 1 ][ 0 ][ i ] = a [ 0 ][ n + 1 ][ i ] = a [ 1 ][ n + 1 ][ i ] = 2 ; for ( int i = 0 ; i <= n + 1 ; i ++ ) a [ 0 ][ i ][ 0 ] = a [ 1 ][ i ][ 0 ] = a [ 0 ][ i ][ m + 1 ] = a [ 1 ][ i ][ m + 1 ] = 2 ; dp [ 0 ][ 0 ][ 0 ] = dp [ 0 ][ 0 ][ 1 ] = 0 ; for ( int i = 1 ; i <= n ; i ++ ) { for ( int j = 0 ; j < 2 ; j ++ ) { for ( int k = 0 ; k < 2 ; k ++ ) { for ( int l = 0 ; l < 2 ; l ++ ) { bool ff = false ; for ( int x = 1 ; x <= m ; x ++ ) ff |= check ( a [ k ][ i ][ x - 1 ], a [ k ][ i ][ x + 1 ], a [ j ][ i - 1 ][ x ], a [ l ][ i + 1 ][ x ], a [ k ][ i ][ x ]); if ( ! ff ) dp [ i ][ k ][ l ] = min ( dp [ i ][ k ][ l ], dp [ i - 1 ][ j ][ k ] + k ); } } } } int ans = min ( dp [ n ][ 1 ][ 0 ], dp [ n ][ 0 ][ 0 ]); cout << ( ans == inf ? -1 : ans ) << endl ;
return 0 ; } // ()()()(?
// https://www.cnblogs.com/DM11/p/17017957.html
ABC283F - Permutation Distance
给定一个排列 \(p\) ,对于每个 \(i\) 求 \(\min\limits_{j \not ={i}}\{|p_i - p_j| + |i - j|\}\) 。
\(1\le n \le 1.5e5\) 。
感觉这种暴力是扫一遍所有的东西求最值的,一定会有一个性质用来排除冗杂状态。
这里还有对于所有 \(i\) 询问一个类似的柿子的东西,也有可能是要枚举贡献。
然后我还不会。
发现绝对值很麻烦,于是我们拆开来看(不要害怕分讨);
如果 \(P_i > P_j\) :
1. 如果 \(i > j\) ,问题转化为求 \(\min\{(p_i+i) - (p_j+j)\}\)
2. 如果 \(i < j\) ,问题转化为求 \(\min\{(p_i-i) - (p_j-j)\}\)
如果 \(P_i < P_j\) :
1. 如果 \(i > j\) ,问题转化为求 \(\min\{(-p_i+i) - (-p_j+j)\}\)
2. 如果 \(i < j\) ,问题转化为求 \(\min\{(-p_i-i) - (-p_j-j)\}\)
其实对于固定的 \(i\) ,我们只需要让后面那坨 \(j\) 相关的柿子尽量大。
好,然后发现这里有两个条件限制,比较麻烦,因为两重限制是不好处理的。
如果单独来算这两个条件是很方便的,这个下标限制就直接 RMQ 或者扫一遍记录,值域限制是经典的一个小模型,可以在值域上利用树状数组动态维护前缀最值来做。
所以我们想要做的是把这两个条件分开算,有点类似单调队列优化 dp 那种,固定一个,处理一个这样子。
所以可以考虑先从前往后枚举 \(i\) ,然后从后往前枚举 \(i\) ,这个相当于满足下标限制。
然后每次扫的时候用两个树状数组维护一下值域上的前/后缀最值即可。
这个套路是 wcx 老师教的,听说这个东西就是二维数点,有必要学一下。
卧槽,写出来简单调一下 1A 了
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72 // author : black_trees
#include <cmath> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #define endl '\n'
using namespace std ; using i64 = long long ; const int si = 2e5 + 10 ; const int inf = 0x3f3f3f3f ; int n , p [ si ]; inline int lowbit ( int x ) { return x & - x ; } struct Fenwick { int t [ si ]; void Init () { memset ( t , -0x3f , sizeof t ); } void Add ( int x , int v ) {
while ( x <= n ) { t [ x ] = max ( t [ x ], v ); x += lowbit ( x ); } } int Que ( int x ) { int ret = - inf ; // ! !!!!!
while ( x ) { ret = max ( ret , t [ x ]); x -= lowbit ( x ); } return ret ; } } pf , sf ; int res [ si ]; int main () { cin . tie ( 0 ) -> sync_with_stdio ( false ); cin . exceptions ( cin . failbit | cin . badbit ); pf . Init (), sf . Init (); cin >> n , memset ( res , 0x3f , sizeof res );
for ( int i = 1 ; i <= n ; ++ i ) cin >> p [ i ]; // i > j
for ( int i = 1 ; i <= n ; ++ i ) { int ans = inf ; ans = min ( ans , p [ i ] + i - pf . Que ( p [ i ])); // prefix
ans = min ( ans , - p [ i ] + i - sf . Que ( n - p [ i ] + 1 )); // suffix
res [ i ] = min ( res [ i ], ans ); pf . Add ( p [ i ], p [ i ] + i ), sf . Add ( n - p [ i ] + 1 , - p [ i ] + i );
} // i < j
pf . Init (), sf . Init (); for ( int i = n ; i >= 1 ; -- i ) { int ans = inf ; ans = min ( ans , p [ i ] - i - pf . Que ( p [ i ])); // prefix
ans = min ( ans , - p [ i ] - i - sf . Que ( n - p [ i ] + 1 )); // suffix
res [ i ] = min ( res [ i ], ans ); pf . Add ( p [ i ], p [ i ] - i ), sf . Add ( n - p [ i ] + 1 , - p [ i ] - i ); } for ( int i = 1 ; i <= n ; ++ i ) cout << res [ i ] << " \n " [ i == n ]; return 0 ; } // ()()()(?
最后更新:
May 9, 2023