ATC & CF 选做(22May)

五月好题改错ψ(｀∇´)ψ

CF1670E Hemose on the Treeψ(｀∇´)ψ

给你 \(n = 2^p\) 个节点的一棵树，你需要为所有点和边一个权值 \(v\)。

且 \(\forall v \in [1, 2^{n + 1} - 1]\)。

你可以任意选择一个根，要求根到所有边或者点的路径上点和边的权值的异或和的最大值最小。

\(p \le 17\)。

可以通过模拟样例发现一个结论：

异或和的最大值最小必定为 \(n\)。

为啥呢？

你考虑对于 \(\forall x < n\)，\(x + n \operatorname{XOR} x\) 是不是必然等于 \(n\)？

然后两对这样的数异或起来就变成了 \(0\)。

然后我们让异或和为 \(0\) 之后，在让 \(0\) 先和一个 \(x\) 异或，然后再和一个 \(x + n\) 异或，那么这个异或和永远不会超过 \(n\)。

所以我们钦定根结点为 \(1\)，权值为 \(n\)，深度为 \(0\)。

然后对于奇数深度节点，权值设为 \(x\)，到父亲的边设为 \(x + n\)。

然后偶数节点反过来。

就构造完了。

Code

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define meow(x) cerr << #x << " = " << x

using namespace std;
using i64 = long long;

const int si = (1 << 18);

int n, p;
int tot = 0, head[si];
struct Edge {
    int ver, Next;
}e[si << 1];
inline void add(int u, int v) {
    e[tot] = (Edge){v, head[u]}, head[u] = tot++;
}

int cnt = 0;
int a[si], c[si << 1];

void dfs(int u, int in_edge, int dep) {
    if(in_edge != -1) {
        ++cnt;
        if(dep % 2 == 0) 
            a[u] = cnt + n, c[in_edge] = cnt;
        else 
            a[u] = cnt, c[in_edge] = cnt + n;
    }
    for(int i = head[u]; ~i; i = e[i].Next) {
        int v = e[i].ver;
        if((i ^ 1) != in_edge) 
            dfs(v, i, dep + 1);
    }
}

int main() {    

    cin.tie(0) -> sync_with_stdio(false);
    cin.exceptions(cin.failbit | cin.badbit);

    int T; cin >> T;
    memset(head, -1, sizeof head);
    while(T--) {
        cnt = tot = 0;
        cin >> p, n = 1 << p;
        for(int i = 1; i < n; ++i) {
            int u, v; 
            cin >> u >> v;
            add(u, v), add(v, u);
        }

        a[1] = n;
        dfs(1, -1, 0);
        cout << "1" << endl;

        for(int i = 1; i <= n; ++i) 
            cout << a[i] << " ",
            head[i] = -1;
        cout << endl;
        for(int i = 0; i < tot; i += 2) 
            cout << c[i] + c[i ^ 1] << " ",
            c[i] = c[i ^ 1] = 0;
        cout << endl;
    }

    return 0;
}

Tag : 构造/树/异或

CF1670F Jee, You See?ψ(｀∇´)ψ

给定 \(n, l, r, z\)，问有多少个长度为 \(n\) 的序列 \(a\) 使得

\(\sum a \in [l, r]\)，且 \(\operatorname{XOR}_i a_i = z\)。

\(n \le 1000, 1\le l, r, z \le 10^{18}\)。

发现这个异或不太好处理。

考虑到二进制底下处理。

我们可以利用一个类似数位 DP 的过程。

只需要能求出任意 \(\sum a \le z\) 的解，就可以用前缀和的思想计算。

最终答案的异或的某一位是否为 \(1\) 只和 \(a\) 中所有数二进制下在这一位的 \(1\) 的个数和前面的进位有关。

而 \(z\) 实际上可以决定每一位最多填多少个 \(1\)。

那么假设 \(z\) 的某一位是 \(1\)

那么所有 \(a\) 中的数二进制下这一位最多一个 \(1\)。

但是因为由进位放到更低的一位就最多两个 \(1\)。

然后以此类推，可以发现每一位最多只能有 \(n\) 个 \(1\)，可以记忆化了。

所以我们设出一个函数 int dfs(int x, int rest, i64 limit)。

表示当前填到 \(x\) 位，之前的位可能选择不填完，于是到这里就剩了 \(rest\) 个 \(1\) 可以填，当前要求 \(\le limit\) 的方案数。

然后枚举这一位填多少一，往下走即可，方案数求一下组合数即可。

注意 \(rest\) 要和 \(n\) 取 \(min\)。

Code

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define meow(x) cerr << #x << " = " << x

using namespace std;
using i64 = long long;

const int si = 1e3 + 10;
constexpr i64 mod = 1ll * (1e9 + 7);

int n;
i64 l, r, z;
i64 f[60 + 10][si];

i64 C[si][si]; // 组合数

// 当前位，上一位剩了多少个 1，要求的答案 
i64 dfs(int x, int rest, i64 val) {
    if(x == -1) return 1;
    // 最低位是 0，所以 x = -1 才是边界。
    if(f[x][rest] != -1) return f[x][rest];

    int a = z >> x & 1, b = (rest << 1) + (val >> x & 1);

    int up = min(b, n); i64 kot = 0;
    // a数组所有的数，这一位最多有 n 个 1，要取 min。
    for(int i = a; i <= up; i += 2) {
        // 上界是 $a$ 是为了保证这位在最后的异或和里和 $z$ 的这一位相同。
        // 每次加 $2$ 是为保证这一位不变。
        kot = (kot + dfs(x - 1, min(n, b - i), val) * C[n][i] % mod) % mod; 
    }
    // 记忆化
    f[x][rest] = kot;
    return kot;
}

i64 solve(i64 val) {
    memset(f, -1, sizeof f);
    return dfs(60, 0, val) % mod;
}

int main() {    

    cin.tie(0) -> sync_with_stdio(false);
    cin.exceptions(cin.failbit | cin.badbit);

    cin >> n >> l >> r >> z;

    C[0][0] = 1ll;
    for(int i = 1; i <= n; ++i) {
        C[i][0] = 1ll;
        for(int j = 1; j <= i; ++j) {
            C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % mod;
        }   
    }

    // meow(solve(5)) << " ", meow(solve(0)) << endl;

    cout << (solve(r) - solve(l - 1) + mod) % mod << endl;

    return 0;
}

Tag : 二进制下的数位DP/异或

CF1684E MEX vs DIFFψ(｀∇´)ψ

定义 \(MEX(A)\) 为序列 \(A\) 中最小的不存在的非负整数。

定义 \(DIFF(A)\) 为序列 \(A\) 中不同的数的个数。

你有 \(k\) 次操作，每次可以把任意一个位置改为任意一个非负整数。

求可以达到的 \(\min\{DIFF(A) - MEX(A)\}\)。

\(1\le n \le 10^5, 0\le k \le 10^5, a_i \le 10^9\)。

发现我们要做的就是最大化 \(MEX\) 并最小化 \(DIFF\)。

有两个变量的话会很不好搞，所以我们尝试固定一个变量。

有一个显然但是我赛时没想到的结论：\(MEX\) 一定 \(\le n + 1\)。

所以我们可以考虑直接枚举 \(MEX\)。

所以要做的就是最小化 \(DIFF\)。

当然对于每个 \(MEX\)，如果它前面（在值域上）有空缺，我们是需要补上的。

如果 \(k\) 次不够的话，这个 \(MEX\) 必然不合法。

然后假设填完空缺还剩下 \(rest\) 次操作机会。

考虑一个比较 trivial 的 greedy，每次操作都尽量让出现次数少的一种数全部变为任意一个前面（\(0 \sim MEX - 1\)）已经出现的数。

每次 \(DIFF\) 能减少一。

然后这样就能最小化 \(DIFF\)。

但是直接暴力做的话复杂度是 \(O(nk)\) 的，考虑怎么优化。

可以考虑记一个数组 \(cnt\) 表示原序列的桶，然后记 \(cntt\) 为 \(cnt\) 的桶。

这样直接在排序过后的 \(cntt\) 尽量取前面的就行。

最坏情况下要取 \(\sqrt{k}\) 次，所以时间复杂度是 \(O(n\sqrt{k})\)。

（因为 \(\dfrac{x(x + 1)}{2} \le k\)，所以项数 \(x\) 是 \(\sqrt{k}\) 级别的。）

Code

// author : black_trees

#include <map>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>

#pragma GCC target("avx,sse2,sse3,sse4,mmx")
#pragma GCC optimize("Ofast", "inline", "-ffast-math")

#define endl '\n'
#define meow(x) cerr << #x << " = " << x

using namespace std;
using i64 = long long;

int main() {    

    cin.tie(0) -> sync_with_stdio(false);
    cin.exceptions(cin.failbit | cin.badbit);

    int T; cin >> T;
    while(T--) {
        int n, k; cin >> n >> k;
        std::map<int, int> cnt; cnt.clear();
        std::map<int, int> cntOfcnt; cntOfcnt.clear();
        std::vector<int> a(n + 1), occ(n + 1); occ.clear(), a.clear();
        for(int i = 1; i <= n; ++i) {
            cin >> a[i], cnt[a[i]]++;
            if(a[i] <= n) occ[a[i]] = 1;
        }
        for(int i = 1; i <= n; ++i) occ[i] += occ[i - 1];
        for(auto [ele, num] : cnt) cntOfcnt[num]++;

        int diff = int(cnt.size()), ans = diff;

        for(int mex = 1; mex <= n + 1; mex++) {
            if(cnt[mex - 1]) cntOfcnt[cnt[mex - 1]] --, diff --;
            if(mex > occ[mex - 1] + k) continue;

            int ret = diff, rest = k;
            for(auto [x, y] : cntOfcnt) {
                if(rest >= x * y) rest -= x * y, ret -= y;
                else { ret -= rest / x; break; }
            }
            ans = min(ans, ret);
        }
        cout << ans << endl;
    }

    return 0;
}

CF1682E Unordered Swapsψ(｀∇´)ψ

给你一个 \(1 \sim n\) 的排列 \(p\)，每次操作可以交换任意两个元素。

Alice 用了最少的操作次数把 \(p\) 置换成了一个有序的排列，即 \(1,2,3,\dots, n\)。

并且 Alice 记录下了她每次的操作 \((x_i, y_i)\)，即交换 \(p_{x_i}, p_{y_i}\)。

但是 Bob 把这个操作二元组序列 \(q\) 打乱了，你需要恢复这个二元组序列的顺序。

并且输出，第 \(i\) 次操作使用的是给定 \(q\) 的第几个二元组，任意解即可。

\(n \le 2e5\)。

又是一道置换环的题。

显然先找出所有的置换环，这个 Tarjan 一下即可。

然后每次操作肯定是交换一个置换环上的两个元素以把置换环拆成两个置换环。

最后的目的就是把所有置换环全部拆成自环。

所以操作时 \(x_i,y_i\) 必须要在同一个置换环上（结论1），否则你就会浪费一次机会，永远无法完成这个置换。

然后我们考虑怎么处理 \(q\)。

可以把一个二元组 \((x_i, y_i)\) 看成一条连接 \((x_i, y_i)\) 的边。

然后对于每一个置换环，它必然会形成一棵树 \(T\)，假设节点个数为 \(N\)。

然后我们要做的就是以某种顺序取这 \(N - 1\) 条边。

此时就没有任何思路了，所以考虑怎么利用一下已经有的结论1。

首先，如果我们选了 \(T\) 上的某个操作 \((u, v)\)，那么实际上等同于删除边 \((u, v)\)，让置换环断成两个。

\(T\) 同样也会分裂成 \(T1, T2\) 两棵树。

但是每一次删除不一定都是合法的，你需要保证断开之后，\(u\) 连通块的都在一个环上，\(v\) 连通块同理。

比如这种情况：

o----o----o----o
1    2    4    3 (Tree)

1    2    3    4 (Ring)
o--->o--->o--->o
^              |
|______________|

你如果删掉 \(T\) 上的边 \((1, 2)\)，那么置换环会变成这样：

1    2    3    4
___________
|         v
o    o    o--->o 
^              |
|______________|

也就是说，独立的连通块变成了 \(2\) 这个节点！。

而本来期望中应该是 \(1\) 这个节点独立出来的。

所以这样的一次操作是不合法的。

思考一下为什么。

发现删掉 \((2, 4)\) 这条边是合法的，之后再删 \((1, 2)\) 这条边就合法了！

不妨猜测，这个选边的顺序可能有什么结论。

结论2

对于一个树上的节点 \(u\)，假设和它有连边的节点集合为 \(adj = \{x_1, x_2, \dots, x_M\}\)。

并且定义 \(dis(u, x)\) 为置换环上 \(u\) 到 \(x\) 的距离。

对 \(adj\) 按照 \(dis(u, x)\) 从小到大排序得到一个新的 \(adj = \{y_1, y_2, \dots, y_M\}\)。

那么，当 \(i < j\) 时，操作 \((u, y_i)\) 必须在 \((u, y_j)\) 之前进行。

否则，如果先进行了 \((u, y_j)\)，那么它一定是一个不合法的操作。

Proof

这个比较好证明，因为你如果先换了 \((u, y_j)\)，那么 \((u, y_i)\) 必然会处在两个不同的置换环上。

为什么会在两个不同的置换环上

设 \(nxt(qwq)\) 表示节点 \(qwq\) 在置换环上指向的节点。

交换 \((u, y_j)\) 之后，\(nxt(u)\) 会变成 \(nxt(y_j)\)，\(nxt(y_i)\) 会变成 \(nxt(u)\)。

然后 \(u\) 就会和原来的 \(nxt(y_j)\) 在一个置换环 \(g_1\) 上，然后原来的 \(nxt(u)\) 一直到 \(y_j\) 这一段都会在另一个置换环 \(g_2\) 上，

并且因为 \(i < j\)，所以 \(y_i\) 也会在 \(g_2\) 上，那么 \(u, y_i\) 自然就是在两个不同的置换环上了。

有一张图可以参考：

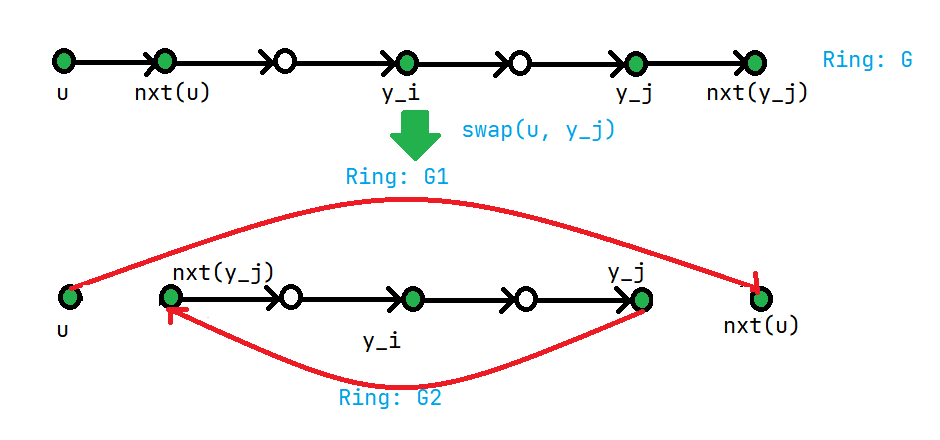
然后你之后再换 \((u, y_i)\) 就会合并两个环，就浪费了一次操作，违背了结论1，永远无法完成置换。

然后发现，其实我们已经能确定某些边的顺序关系了，我们定义一种新的关系 \((x, y) \prec (xx, yy)\)，表示我们能确定 \((x, y)\) 这个操作比 \((xx, yy)\) 先使用。

我们发现，对于树上每个度数大于一的节点 \(u\)，和他相关的所有边如果构成集合 \(E_u\)，那么 \(E_u\) 中的所有元素必然会以链式的形式满足关系 \(\prec\)。

然后不同的两个集合 \(E1, E2\)，必然会以一个 \(\prec\) 关系连接起来（因为这是树啊）

而且不会有重复的两对关系出现。

思考一下，\(\prec\) 这个关系其实就是一个严格偏序关系，我们可以利用拓扑求它的解。

而我们要求的正好就是这些边的使用顺序。

所以我们可以把这些边看作节点，对于树上的一个节点 \(u\)，我们令 \(adj_u = \{x_1, x_2, \dots\}\)。

那么，只需要连 \((u, x_1) \to (u, x_2) \to (u, x_3) \to \dots\)。

最后跑一个拓扑排序就行了。

注意这里的点对 \((x, y)\) 应当是无序的，所以有个小技巧就是，每次操作的时候强制 \(x < y\) 以方便处理。

Code

// author : black_trees

#include <map>
#include <stack>
#include <queue>
#include <cstdio>
#include <vector>
#include <cassert>
#include <cstring>
#include <utility>
#include <iostream>
#include <algorithm>

#pragma GCC target("avx,sse2,sse3,sse4,mmx")
#pragma GCC optimize("Ofast", "inline", "-ffast-math")

#define endl '\n'
#define meow(x) cerr << #x << " = " << x

using namespace std;
using i64 = long long;

const int si = 2e5 + 10;

int n, m;
int tim = 0, cnt = 0;
int p[si]; // 给定的被打乱的 perm
int dfn[si]; // 每个节点(1 ~ n)在找环的时候的 dfs 序。
std::vector<int> G[si]; // 原图的邻接表，用来找环。
std::vector<int> adj[si]; // 树的邻接表

int low[si];
bool ins[si];
std::stack<int>s;
int c[si], maxv[si], minv[si]; // i 所属的环的编号，环上最大最小 dfn.
void tarjan(int u) {
    dfn[u] = low[u] = ++tim;
    s.push(u), ins[u] = false;
    for(auto v : G[u]) {
        if(!dfn[v]) tarjan(v), low[u] = min(low[u], low[v]);
        else low[u] = min(low[u], dfn[v]);
    }
    if(dfn[u] == low[u]) {
        int x; ++cnt;
        do { 
            x = s.top(), s.pop(), c[x] = cnt, 
            maxv[cnt] = max(maxv[cnt], dfn[x]), 
            minv[cnt] = min(minv[cnt], dfn[x]);
        } while(u != x);
    }
}

std::map<pair<int, int>, int> Hash; // 用来记录这条边的编号。

int order = 0; // 最后得到的 topo 序。
int ind[si]; // 入度
struct Node { int u, v, id; } rec[si]; // 记录这个 swap 的属性。
std::vector<int> E[si]; // 用来拓扑的图。

int ans[si], ret[si]; // ans[i] 是第 i 个 swap 的 order
                      // ret[i] 是第 i 次使用哪个 swap。

int main() {    

    cin.tie(0) -> sync_with_stdio(false);
    cin.exceptions(cin.failbit | cin.badbit);

    Hash.clear();
    memset(minv, 0x3f, sizeof minv);
    memset(maxv, -0x3f, sizeof maxv);

    // sort by PosSt
    auto dis = [&](int PosSt, int PosEd) -> int {
        assert(c[PosSt] == c[PosEd]);
        int bel = c[PosSt];
        int siz = maxv[bel] - minv[bel] + 1;
        return ((dfn[PosEd] - dfn[PosSt]) + siz) % siz;
    };

    cin >> n >> m;
    for(int i = 1; i <= n; ++i) 
        cin >> p[i], G[i].push_back(p[i]);
    for(int i = 1; i <= n; ++i) 
        if(!dfn[i]) tarjan(i);

    for(int i = 1; i <= m; ++i) {
        int u, v; cin >> u >> v;    // 操作的位置。
        assert(c[u] == c[v]);
        adj[u].push_back(v), adj[v].push_back(u);
        if(u > v) swap(u, v);
        Hash[{u, v}] = i;
        rec[i] = (Node){u, v, i};
    }

    for(int i = 1; i <= n; ++i)
        sort(adj[i].begin(), adj[i].end(), [&](int x, int y) { return dis(i, x) < dis(i, y); }); 
    // 按照结论给 adj 排个序

    for(int i = 1; i <= n; ++i) {
        for(int j = 0; j < int(adj[i].size()) - 1; ++j) {
            int x = i, y = adj[i][j], u = i, v = adj[i][j + 1];
            if(x > y) swap(x, y); 
            if(u > v) swap(u, v);
            int yhp = Hash[{x, y}], zxy = Hash[{u, v}];
            E[yhp].push_back(zxy), ind[zxy]++;
        }
    } 

    std::queue<int> q;
    for(int i = 1; i <= m; ++i) 
        if(!ind[i]) q.push(i);
    while(!q.empty()) {
        int u = q.front(); q.pop();
        ans[rec[u].id] = ++order;
        for(auto v : E[u]) if(!(--ind[v])) q.push(v);
    }

    for(int i = 1; i <= m; ++i)
        ret[i] = i;
    sort(ret + 1, ret + 1 + m, [&](int x, int y){ return ans[x] < ans[y]; });
    for(int i = 1; i <= m; ++i) 
        cout << ret[i] << " ";
    cout << endl;

    return 0;
}
// 其实上面有些东西是不必要的，不过懒得改了，反正意思都一样。

最后更新: May 9, 2023