跳转至

AC 自动机

本文默认读者已经阅读了 字符串基础

没搞懂，我觉得 AC 自动机几句话就讲完了，为啥网上那么多长篇大论。

感觉显然是基础不牢导致的，如果简单学习过自动机理论理解 AC 自动机不是分分钟的事情。

所以我接下来可能会说的很快。

泛化ψ(｀∇´)ψ

基本结构ψ(｀∇´)ψ

AC 自动机是一个多模匹配算法，简单来说支持查询对于给定的模式串集合 \(S\)，查询 \(s_i\) 在文本串 \(t\) 中的出现次数和位置。

它是一个仅接受以 \(S\) 中某个元素作为后缀的字符串的自动机。

为了方便，记 \(str(u)\) 表示 AC 自动机上状态 \(u\) 表示的字符串。

构建ψ(｀∇´)ψ

首先明确目的，我们想要让 AC 自动机接受我们需要的一些字符串，我们看看有没有什么便捷的方式构造出自动机。

注意到 Trie 树实际上是一个，满足我们的部分要求的自动机，它接受给定的模式串集合 \(S\) 中的所有字符串，但是它不接受以模式串作为后缀的字符串。

不妨偷个懒，把 Trie 树拉过来，对 Trie 进行调教，在上面加一些状态转移，并扩展接受状态集合以达到接受作为 \(S\) 中某个元素后缀存在的字符串的目的。

现在我们想要支持接受这样的字符串 \(t\)，实质上是，想要去掉 \(t\) 的一个前缀，使得 \(t\) 的新前缀能和模式串匹配，进而找到模式串在原串中的出现。

所以不妨添加一个失配指针 \(\text{Fail}(u)\)，表示在 \(u\) 这个地方失配的时候的去向。

失配，其实也就是我们找不到一个状态 \(u\) 使得它能和 \(t\) 的一个前缀匹配上了，而我们现在实际上已经处理前缀 \(pre(t, x) = str(u)\) 的影响，等价于是 \(pre(t, x)\) 被我们从 \(t\) 当中“割掉”了，我们只需要找到一个位置，使得它有机会继续匹配 \(t[x + 1]\) 即可。

这样的位置可能有很多，我们不妨定义 \(\text{Fail}(u)\) 为这些位置中，长度最大的那个，这样的话，这些位置就可以通过不断跳 \(\text{Fail}\) 来到达。

换句话说，\(\text{Fail}(u)\) 指向一个状态 \(v\)，使得 \(str(v) = suf(str(u), x)\) 且 \(x\) 最大。

那么构建 \(\text{Fail}\) 就是一个很简单的过程了，我们可以类比 KMP 的 Next 指针。

首先，我们先初始化，让所有的 \(\text{Fail}\) 都指向 \(\text{root}\)（初始状态）。

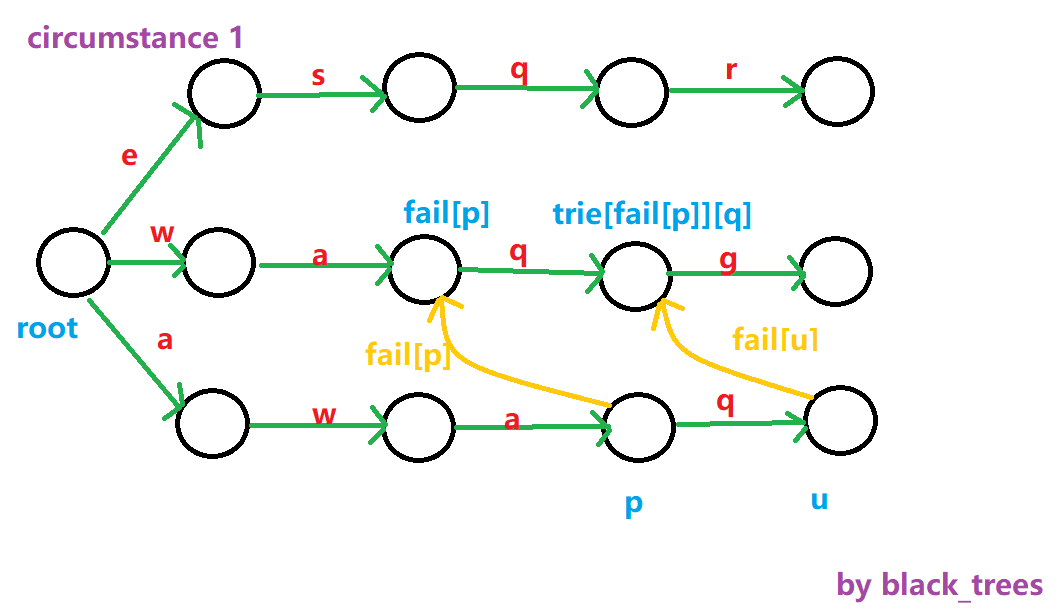
考虑当前节点是 \(u\) ，它的父亲节点是 \(p\) ，并且满足 \(p\) 通过一个字符 \(ch\) 走到 \(u\) 即 \(\text{Trie}[p][ch]=u\)。

并且我们假设深度小于 \(u\) 的所有节点的 \(\text{Fail}\) 都已经通过 BFS 求出。

首先看第一种情况，如果 \(\text{Trie}[\text{Fail}(p)][ch]\) 存在，也就是存在一个从 \(\text{Fail}(p)\) 指出的 \(ch\) 字符的指针指向另外一个状态。

那么我们就直接让 \(\text{Fail}(p)\) 指向 \(\text{Trie}[\text{Fail}(p)][ch]\) 。

因为 \(p\) 这个状态一定是状态 \(u\) 的一个前缀，而 \(\text{Fail}(p)\) 是 \(p\) 的后缀，那么如果 \(\text{Fail}(p)\) 有一个字符指针为 \(ch\) ，那么这个字符指针指向的状态一定是 \(u\) 的后缀。

4XJmxe.png

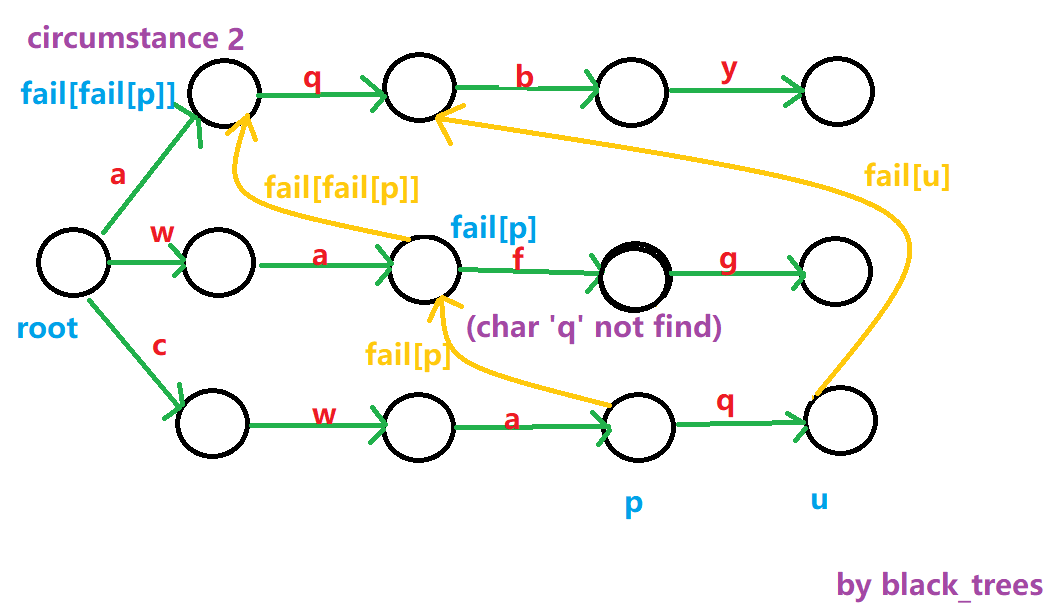
那如果 \(\text{Fail}(p)\) 这个节点没有 \(ch\) 这个字符指针呢？

那我们就用 KMP 的思想，我继续跳 \(\text{Fail}({\text{Fail}(p)}),\text{Fail}({\text{Fail}({\text{Fail}(p)})})...\) ！然后重复第一种情况的判断，直到有 \(ch\) 为止。

4XJe2D.png

如果真的找不到任何一个状态可以作为 \(\text{Fail}(u)\) 的话，我们让 \(\text{Fail}(u)\) 直接指向 \(\text{root}\) 就行，这个已经初始化过了所以不用管。

然后对于多模式查询，我们直接遍历文本串 \(t\)，通过 Trie 进行转移，如果不存在对应字符指针，就跳 \(\text{Fail}\) 再尝试转移就好了。

Trie 图优化ψ(｀∇´)ψ

在对于转移 \(\delta(u, ch)\) 失配的时候，我们只跳一次 \(\text{Fail}\) 通常来说是不够的，因为这里一步不一定能跳到有 \(ch\) 转移的节点。

在精心构造的数据（好像很容易构造来着）下会被卡。

我们考虑优化，想一想，有没有办法直接一步到位，直接对于每个失配的字符，找到对应的能够匹配位置而不用多次跳 \(\text{Fail}\) 呢？

注意到 \(\text{Trie}\) 实际上是作为 AC 自动机的转移函数存在的，它的定义和原来 Trie 树上的定义是一样的，而如果 Trie 上不存在对应的指针，则会使用 \(\text{Fail}\) 指针代替，相当于是我们的转移函数被分类了，而且还要分开求，分开进行转移。

这是坏的，我们考虑整合，记 \(\text{Trans}[u][ch]\) 表示，节点 \(u\) 加上一个字符 \(ch\) 之后应该去向的状态是什么，相当于还额外给 \(\text{Fail}\) 做了一个路径压缩。

假设我们已经求出了比 \(u\) 深度小的节点的 \(\text{Trans \& Fail}\)，现在更新 \(u\)。

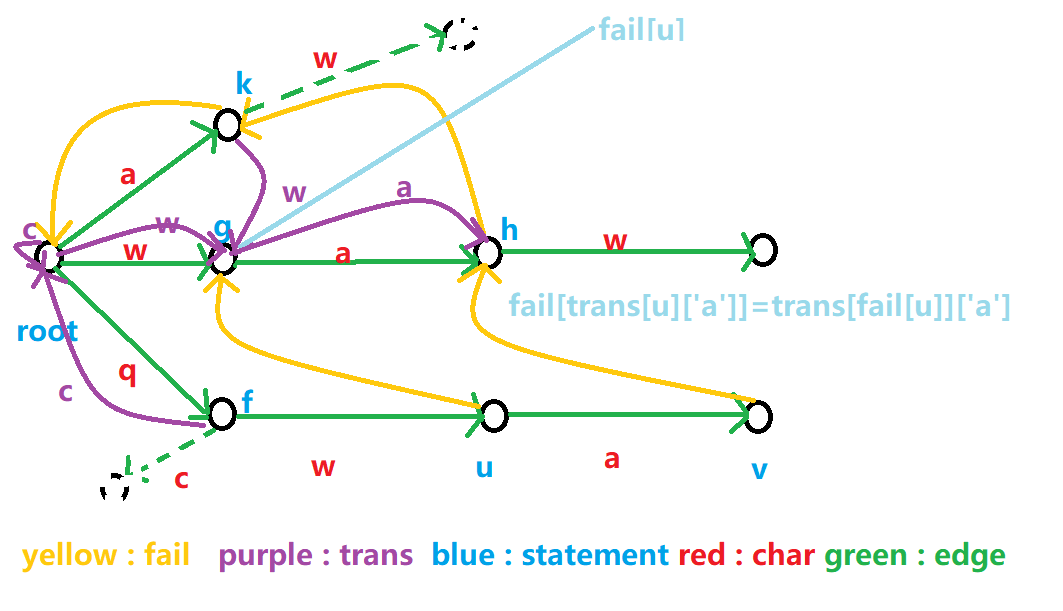
考虑 \(u\) 的每一条转移 \(\text{Trie}[u][ch]\)，如果 \(\text{Trie}[u][ch] \not= \text{NULL}\)，那么说明 \(\text{Trans}[u][ch]\) 代表的就是原来 Trie 树上的 \(\delta(u, ch)\) 的转移，令 \(\text{Trans}[u][ch] \gets \text{Trie}[u][ch]\) 即可，此时还需要更新一下 \(\text{Trans}[u][ch]\) 节点的 \(\text{Fail}\)，令 \(\text{Fail}(\text{Trans}[u][ch]) = \text{Trans}[\text{Fail}(u)][ch]\) 即可，这个和上面没有优化的情况一类似。

由 \(\text{Trans}\) 的定义，我们不需要再多次失配跳 \(\text{Fail}\) 了，\(\text{Trans}\) 已经帮我们完成了这件事。

否则，说明 \(\delta(u, ch)\) 这个转移会失配，而我们现在需要压缩 \(\text{Fail}(u)\) 的路径，鉴于 \(\text{Trans}\) 的定义，我们令 \(\text{Trans}[u][ch] \gets \text{Trans}[\text{Fail}(u)][ch]\) 即可，因为 \(dep(\text{Fail(u)}) < dep(u)\) 所以这个是之前已经求过了的，转移没有问题。

4XJZ8O.png

（这里只画了一小部分 \(\text{Trans}\)）

实现的时候可以直接合并 \(\text{Trie, Trans}\) 两个数组，覆盖一下就可以了。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
std::queue<int> q;
void build() {
    for(int ch = 1; ch <= 26; ++ch) 
        if(tr[0][ch]) q.push(tr[0][ch]);
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        for(int ch = 1; ch <= 26; ++ch) {
            if(tr[u][ch])
                fail[tr[u][ch]] = tr[fail[u]][ch], q.push(tr[u][ch]);
            else tr[u][ch] = tr[fail[u]][ch];
        }
    }
}

复杂度是 \(O(\sum |s_i|)\)。

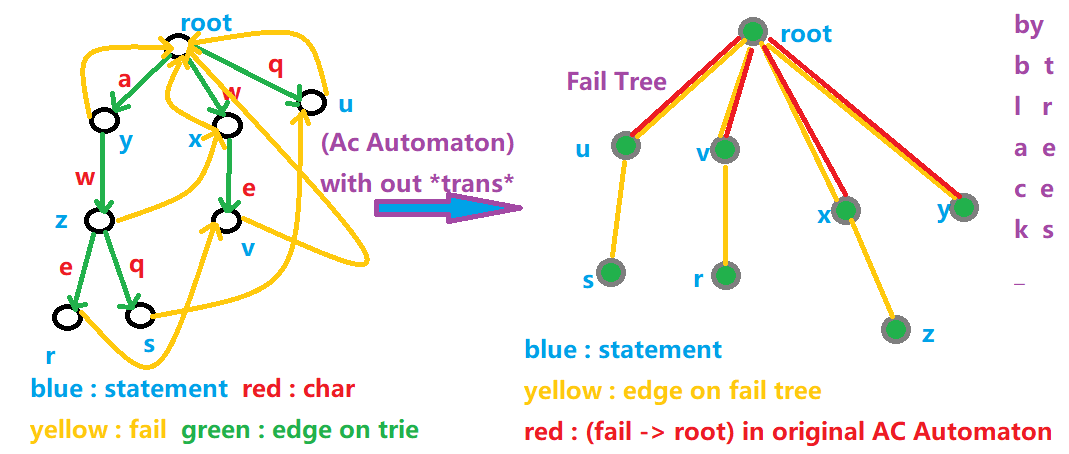
Fail 树ψ(｀∇´)ψ

又是后缀链接树，我们看看它有什么性质。

连边和 KMP 自动机的 Fail 树连边是一样的，\((i,\text{Fail}(i))\)，\(\text{Fail}\) 作为父节点。

4v89SS.png

  • \(u\) 的子树当中的所有节点都有 \(u\) 这个真后缀（注意不一定是最长，只是普通的真后缀）。
    • \(u\) 的所有真后缀，就是 \(u\) 的所有祖先节点所代表的字符串。
  • \(u\) 的子树之外的节点都没有 \(u\) 这个真后缀。

这是显然的，根据 \(\text{Fail}\) 的性质可以得到。

能干啥？

你注意到匹配某个文本串的过程实际上是不断找到一个出现在 \(t\) 中的状态。

而我们现在想要统计每个模式串出现的次数，根据第一个性质，如果我们跳到了 \(u\) 的子树当中某个节点，就证明 \(u\) 出现了一次。

我们可以在每个节点上打个标记，表示它被直接匹配到了多少次，匹配完了 dfs 一下后缀链接树统计答案就行了。

还有更多的应用就看例题好了。

没时间写就之后补。

例题ψ(｀∇´)ψ

Luogu3808 【模板】AC 自动机（简单版）ψ(｀∇´)ψ

只询问是否出现。

考虑每次跳到一个位置的时候暴力跳 \(\text{Fail}\) 统计所有的串。

本质上是遍历了 Fail 树的多条链。

Code 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
// author : black_trees

#include <cmath>
#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define endl '\n'

using namespace std;
using i64 = long long;

const int si = 1e6 + 10;

int n, m;
string s, t;

int end_[si];
int ans = 0, tot = 0;
int tr[si][27], fail[si];
int idx(char ch) { return (int)(ch - 'a' + 1); } 
void insert(string s) {
    m = (int)s.size(), s = ' ' + s;
    int u = 0;
    for(int i = 1; i <= m; ++i) {
        int ch = idx(s[i]);
        if(tr[u][ch]) u = tr[u][ch];
        else tr[u][ch] = ++tot, u = tr[u][ch];
    }
    end_[u] += 1;
}
std::queue<int> q;
void build() {
    for(int ch = 1; ch <= 26; ++ch)
        if(tr[0][ch]) q.push(tr[0][ch]);
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        for(int ch = 1; ch <= 26; ++ch) {
            if(tr[u][ch])
                fail[tr[u][ch]] = tr[fail[u]][ch], q.push(tr[u][ch]);
            else tr[u][ch] = tr[fail[u]][ch];
        }
    }
}
void query(string t) {
    ans = 0;
    m = (int)t.size(), t = ' ' + t;
    int u = 0;
    for(int i = 1; i <= m; ++i) {
        int ch = idx(t[i]);
        u = tr[u][ch];
        for(int j = u; j && ~end_[j]; j = fail[j])
            ans += end_[j], end_[j] = -1;
    }
}

int main() {

    cin.tie(0) -> sync_with_stdio(false);
    cin.exceptions(cin.failbit | cin.badbit);

    tot = 0;
    memset(tr, 0, sizeof tr);
    memset(fail, 0, sizeof fail);
    memset(end_, 0, sizeof end_);

    cin >> n;
    for(int i = 1; i <= n; ++i)
        cin >> s, insert(s);
    cin >> t, build(), query(t);
    cout << ans << endl;

    return 0;
}

Luogu5357 【模板】AC 自动机（二次加强版）ψ(｀∇´)ψ

询问出现次数。

Code 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
// author : black_trees

#include <cmath>
#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define endl '\n'

using namespace std;
using i64 = long long;

const int si = 2e6 + 10;

int n, m;
string s, t;

int end_[si];
int ans = 0, tot = 0;
int tr[si][27], fail[si];
int cur = 0, head[si];
struct Edge { int ver, Next; } e[si << 1];
inline void add(int u, int v) { e[cur] = (Edge){v, head[u]}, head[u] = cur++; }
int idx(char ch) { return (int)(ch - 'a' + 1); } 
void insert(string s, int id) {
    m = (int)s.size(), s = ' ' + s;
    int u = 0;
    for(int i = 1; i <= m; ++i) {
        int ch = idx(s[i]);
        if(tr[u][ch]) u = tr[u][ch];
        else tr[u][ch] = ++tot, u = tr[u][ch];
    }
    end_[id] = u;
}
std::queue<int> q;
void build() {
    for(int ch = 1; ch <= 26; ++ch)
        if(tr[0][ch]) q.push(tr[0][ch]);
    while(!q.empty()) {
        int u = q.front();
        q.pop(), add(fail[u], u);
        for(int ch = 1; ch <= 26; ++ch) {
            if(tr[u][ch])
                fail[tr[u][ch]] = tr[fail[u]][ch], q.push(tr[u][ch]);
            else tr[u][ch] = tr[fail[u]][ch];
        }
    }
}
int cnt[si];
void dfs(int u, int fa) {
    for(int i = head[u]; ~i; i = e[i].Next) {
        int v = e[i].ver;
        if(v == fa) continue;
        dfs(v, u), cnt[u] += cnt[v];
    }
}
void query(string t) {
    m = (int)t.size(), t = ' ' + t;
    int u = 0;
    for(int i = 1; i <= m; ++i) {
        int ch = idx(t[i]);
        u = tr[u][ch], ++cnt[u];
    }
    dfs(0, -1);
    for(int i = 1; i <= n; ++i)
        cout << cnt[end_[i]] << endl;
}

int main() {

    cin.tie(0) -> sync_with_stdio(false);
    cin.exceptions(cin.failbit | cin.badbit);

    tot = 0;
    memset(tr, 0, sizeof tr);
    memset(cnt, 0, sizeof cnt);
    memset(fail, 0, sizeof fail);
    memset(end_, 0, sizeof end_);
    memset(head, -1, sizeof head);

    cin >> n;
    for(int i = 1; i <= n; ++i)
        cin >> s, insert(s, i);
    cin >> t, build(), query(t);

    return 0;
}

[NOI2011] 阿狸的打字机ψ(｀∇´)ψ

Fail 树的基本应用

[JSOI2007] 文本生成器ψ(｀∇´)ψ

这个题算是介绍了 AC 自动机上 DP 相关的大部分套路了。

最后更新: July 16, 2023